СОЕДИНЕНИЕ МЕТАЛЛОВ В ТВЕРДОЙ ФАЗЕ
ПРИМЕРЫ АНАЛИЗА ВЗАИМОДЕЙСТВИЯ МЕТАЛЛОВ С НЕМЕТАЛЛАМИ
Определение термодинамической разрешенности процесса образования химических связей при различных окружающих средах наиболее интересно в случае соединения разнородных материалов, имеющих различный тип связи (например, соединение металлов с окислами и другими неметаллическими материалами).
Для оценки общих закономерностей возможности соединения керамических материалов с металлами можно воспользоваться методикой, изложенной в работе [43]. В общем случае характер взаимодействия окисла с металлом может быть определен из уравнения [44]
Me' + Me" О = Me' О + Me", (1)
что термодинамически может быть выражено как
AZ =AZAte'o—AZmc"o - (2)
Очевидно, при AZ° > 0 взаимодействие невозможно, а при AZ° < 0 взаимодействие возможно.
Анализ данных расчета по уравнению (2) позволяет произвести оценку возможности и характера взаимодействия между окислами и металлами различной природы.
С целью ограничения числа возможных сочетаний металл + + керамика представляется целесообразным отдельно рассмотреть такие металлы и окислы, которые наиболее часто используются в металлокерамических конструкциях.
Металлы. В табл. 1 приведены температуры плавления рассматриваемых металлов и значения AZ° их окислов при 1000 и 1800° С.
|
ТЕМПЕРАТУРЫ ПЛАВЛЕНИЯ НЕКОТОРЫХ МЕТАЛЛОВ И ЗНАЧЕНИЯ ДZ° ИХ ОКИСЛОВ
|
Исходя из условия устойчивости к окислению металла, наиболее выгодно максимальное значение AZ° (минимальное по абсолютной величине). В связи с этим необходимо сопоставить значения AZ° для окислов приведенных выше металлов, которые условно отнесем к 1-й группе.
Анализ данных табл. 1 позволяет составить ряд по возрастанию способности металлов к окислению:
NiO, СоО, W03, Мо02, Сг203, NbO, Ta205, V203, ТЮ2, А1203, Zr02.
Окиспы. В качестве окислов рассмотрим те из них, которые, как правило, являются или основой керамик, или наиболее часто входят в состав керамических материалов.
С точки зрения диссоциации окислов наиболее выгодно минимальное значение AZ0 (максимальное по абсолютной величине). В табл. 2 приведены значения AZ“ и энергоемкости для ряда окислов. Условно отнесем эти окислы ко 2-й группе.
|
Таблица 2 ЗНАЧЕНИЯ Д2° НЕКОТОРЫХ ОКИСЛОВ
|
Анализ данных табл. 2 показывает, что последовательность уменьшения устойчивости исследуемых окислов может быть выражена следующим рядом: ТЮ2, CaO, BeO, MgO, Zr02, V02, А1203> Si02, Cr203.
Анализ полученных рядов активности позволяет определить общие закономерности термодинамического взаимодействия металлов с окислами.
С точки зрения предпочтительности взаимодействия целесообразно брать пары, состоящие из комбинаций окислов с минимальным значением AZ° для 1-й группы окислов и максимальным значением AZ° для 2-й группы окислов. Сказанное может быть проиллюстрировано следующей схемой:
|
*Сг..О, |
|
|
(- СУ |
Si02 |
|
CJ |
А12о3 |
|
Он да |
VOo |
|
^ да о ь |
Zr02 |
|
* О О * |
MgO |
|
^ ю 5 |
BeO |
|
* |
CaO |
|
ThO |
|
Металлы Активность растет |
Эта схема взаимодействия окислов с металлами находится в полном соответствии с данными работы [451, где на основе термодинамических расчетов определен аналогичный ряд активности.
Данная схема взаимодействия справедлива в случае ведения процесса в сверхвысоком вакууме или в случае восстановительной атмосферы. Осуществление процесса соединения в вакууме 10“4 — 10'5 мм рт. ст. должно внести корректировку в последовательность активности металлов по отношению к окислам. Это хорошо подтверждается экспериментальными исследованиями, которые показывают, что керамика на основе А1203 образует соединение с никелем гораздо легче, чем с танталом или ниобием.
Термодинамический анализ процесса взаимодействия, например А1203 с ниобием [45], показал, что при взаимодействии окись алюминия восстанавливается до AI и ALO, а ниобий окисляется до высшего окисла Nb205. Суммарное давление газообразных продуктов взаимодействия А1203 с ниобием при 2000 К составляет 2,22 • 10_6 ат. Последнее позволяет определить температуру начала взаимодействия, за которую принята температура, при которой сумма парциальных давлений равна давлению окружающей среды. Исходя из этого определения, температура начала взаимодействия А1203 с ниобием определяется давлением окружающей среды. По мере понижения давления окружающей среды температуры начала взаимодействия снижается.
Согласно данным работы 145], зависимость температуры начала взаимодействия от давления окружающей среды в системе А1203— Nb имеет следующий вид:
Давление среды, ат 10-8 10'7 10"6 10'6 10'4
Температура, К............................................... 1670 1800 1950 2100 2300
Воспользовавшись этой зависимостью, можно при известном давлении окружающей среды выбирать минимальное значение температуры сварки окиси алюминия с ниобием.
Основной трудностью при термодинамических оценках взаимодействия материалов в твердой фазе является отсутствие данных изобарно-изотермических потенциалов компонентов реакции при различных температурах. Поэтому при решении конкретной термодинамической задачи следует пользоваться приемами и методами, разработанными в термодинамике для определения AZJ.
Например, при решении задачи выбора металла для соединения с кварцем (Si02) может быть использован следующий подход 146].
|
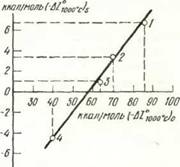
Рнс 5. Графическая зависимость изобарно-изотермических потенциалов образования окислов и силикатов некоторых металлов при 1000° С: |
В качестве металлов будем рассматривать железо, кобальт, никель и медь. В литературе приводятся значения AZiooo°с Для силикатов железа, кобальта и никеля, однако таких данных нет для силиката меди. Поэтому для оценочного определения целесообразно воспользоваться методом сравнительного расчета, предложенным в работе [47]. По этому методу значения AZjooo°c Для силикатов железа, кобальта и никеля следует сопоставлять со значениями изобарно-изотермических потенциалов при той же температуре для соответствующих окислов FeO, СоО, NiO и Си20. При графическом построении соотношения AZiooo»c Для силикатов и окислов выбранных металлов довольно точно подчиняются линейной зависимости (рис. 5). Таким образом, можно определить значение AZiooo° с Для силиката меди Cu2Si04, возможность образования которого при твердофазных реакциях допускается в работе [48].
(Необходимые данные при построении графика на рис. 5 заимствованы из работы [43]).
Аналогичный подход может быть использован при решении частных термодинамических задач, когда, например, требуется соединять материалы, для которых необходимых данных в литературе недостаточно.
|
1 — Fe; 2 — Со; 3 — Ni; 4 — Си |
Исследования по сварке давлением с подогревом разнородных материалов показывают, что физико-химическое взаимодействие
в контакте соединяемых материалов сопровождается образованием промежуточного слоя, который может быть твердым раствором переменного состава или новым химическим соединением.
Этот переходный слой появляется в результате протекания контактной реакции, скорость которой определяется быстротой протекания процесса образования химических связей и последующих кристаллохимических и диффузионных процессов в приповерхностных слоях свариваемых материалов, если образуется новое химическое соединение, и только диффузионных процессов — если образуется твердый раствор.
При сварке металлических материалов с неметаллическими переход от решетки неметалла с ионно-ковалентными связями к металлической решетке металла тем более не может быть скачкообразным. Очевидно, этот переход для получения достаточно прочного соединения должен осуществляться в какой-то мере постепенно, через промежуточные фазы. Структуру поверхности раздела между промежуточными и исходными фазами можно сравнить, например, с таковой между металлом и его окислом, хотя и в этом случае природа связей между этими фазами в настоящее время практически неизвестна [41 ].
Процесс образования новой фазы идет в том случае, если это энергетически выгодно, т. е. приводит к уменьшению свободной энергии системы; последнее можно оценить проведением термодинамического анализа возможности протекания химической реакции между свариваемыми материалами по методикам, использованным в работах [46, 49].
Термодинамический анализ позволяет теоретически исследовать фазовый состав переходной зоны, поскольку сварка давлением с подогревом, в отличие от других способов соединения в твердой фазе, протекает при достаточно высоких температурах и достаточно длительное время для того, чтобы успели образоваться устойчивые в этих условиях фазы [31].
В отличие от термодинамического анализа известной химиче - ческой реакции, при диффузионной сварке в суммарном уравнении известны лишь исходные вещества, т. е. свариваемые материалы, и лишь предположительно — продукты, которые могут образоваться в переходном слое. Это вызывает необходимость производить термодинамический анализ возможности взаимодействия по ряду уравнений, в которых левая часть—-исходные вещества, а в правой части каждого уравнения находятся разные вещества, образование которых можно предположить.
При сварке сульфидной керамики ZnS с медью взаимодействие возможно по реакциям [50]:
|
(3) (4) (5) |
ZnS + Си = CuS + Zn, ZnS - f 2Cu = Cu2S + Zn, ZnS + 3Cu Cu2S -|- CuZn.
|
ЗНАЧЕНИЯ ДZ РЕАКЦИЙ (3), (4) И (5) ПРИ РАЗЛИЧНЫХ ТЕМПЕРАТУРАХ
|
Результаты расчетов изобарно-изотермических потенциалов при различных температурах для реакций (3), (4) и (5) приведены в табл. 3 (данные, необходимые для расчетов, заимствованы из работ [51—53]).
Анализ данных табл. 3 показывает, что при всех исследуемых температурах AZ° положительно, следовательно, ни по одной из приведенных реакций взаимодействие невозможно.
Однако прямая химическая реакция типа реакций (3), (4) и
(5) не единственный вид взаимодействия разнородных материалов. В работах [54—56] показано, что когда взаимодействие неметаллических материалов с металлами характеризуется высокими значениями изменений свободной энергии, то при невозможности прямой реакции взаимодействие возможно за счет образования твердых растворов.
Используя подход, примененный в работе [56], взаимодействие сульфидной керамики ZnS с медью можно рассчитать, приняв в качестве основы для термодинамических расчетов реакцию
ZnS(TB) = [ZnJcu + [S]c, (6)
где ZnS(TB) — твердое вещество;
[Zn lCu — твердый раствор серы в меди.
Реакцию (6) можно представить в виде трех след} ющих последовательных реакций:
TOC o "1-5" h z ZnS(TB) =Zn(TB) - j ^2(тв) » (7)
-i-S2(TB,=[S]cu, (8)
Zn(TB) = [Zn]Cu - (9)
В равновесных условиях сумма изобарных потенциалов этих
реакций равна нулю, т. е.
AZ<6) =AZ(7, —J— AZ(8) + AZ(9) =0. (19)
Поскольку цинк в этих реакциях участвует в качестве промежуточного продукта, его агрегатное состояние можно не учитывать. Можно условно принять, что во всех реакциях он находится в твердой фазе. Будем использовать формулу изобарного потенциала разложения ZnS(TB) с образованием Zn(TB) и формулу изобарного потенциала растворения Zn(TB) в металле. Полученный результат в первом приближении будет верен и для температур выше температуры плавления цинка.
AZ(7, = 63,65 + 4,6-10’sTgT—36,68-10 3Г.
Изменение изобарного потенциала при растворении чистого вещества (серы) с образованием в меди разбавленного раствора выражается уравнением [56]:
|
(И) |
AZ,8, = ДЯ(8) +ВГ + 4.57Г lgtfs,
где Ns — атомная доля серы в растворе.
В уравнении (11) величины АЯ(8) и В не зависят от температуры и концентрации. Их можно определить, если известна растворимость серы в меди минимум при двух температурах и если для этих температур можно рассчитать изменение свободной энергии образования низшего сульфида меди, находящегося в равновесии с твердым раствором серы в меди.
Насыщенный твердый раствор находится в равновесии с сульфидом, поэтому для реакции
[S]L + [Сиь
|
(12) |
Cu2S
изменение изобарного потенциала AZ(9) = 0.
Реакцию (12) можно представить в виде последовательных реакций:
CU-iS = 2CU(TB) -) 2~S2(ra3)>-------------------------- (13)
|
2 ^2 (газ) [S]Cu > 2Cu(TB) [CuJcu. Для этих реакций AZ(12) AZ(13) + AZ(14) + AZ(15, = 0. |
1
(14)
(15)
(16)
|
(17) |
|
(8). |
|
AZ(i3> — — AZ(14) — — AZ( |
|
Реакция (14) полностью аналогична реакции (8), т. е. для реакции (14) также применимо уравнение (11), что дает основание использовать равенство (17) для определения величин АЯ(8) и В в уравнении (11). |
При введении разбавителя в разбавленный раствор изменение изобарного потенциала мало, поэтому можно принять AZ(iS) = 0 и, следовательно:
Значення ДЯ(8) и В можно определить из соотношения (17), записанного для двух температур:
— AZ(i3) (Гі) = АЯ(в) + ВТ + 4,577’i lg Л/£ (Г,), (18)
-Аг(,з,(Г2) = АЯ(8) +fi7’2 + 4,577’2lg^|I(r2). (19)
Изменение изобарного потенциала —AZ(i3) образования низшего сульфида меди можно подсчитать по формуле [51]:
AZ(i3> = — AZCUss = 34,15 + 6,22 • 10 3Т lg Т — 28,74 • 10 3Г.
Данные по растворимости серы в меди известны для двух температур [56]:
при 7 = 600° С 0,0005% (по массе) S или 0,001% (ат.) или — = 0,00001.
при Т2 = 800° С 0,002% (по массе) S или 0,004% (ат.) или Ns — = 0,00004.
Данные по растворимости и вычисленные значения изменения изобарных потенциалов для температур, при которых известна растворимость, подставим в уравнения (18) и (19):
— 25 000 = АЯ(8) + В • 873 + 4,57 • 873 lg 0,00001;
— 23 500 = ДЯ(8) -[-В-1073 + 4,57 • 1073 lg 0,00004.
Из этих уравнений получаем:
ДЯ8 =—18,5 ккал/г-атом,
В — +15,5 кал/(°С*г-атом).
Рассчитанная величина АН{&) близка к теплоте образования Cu2S (—19,0 — 0,5 ккал/г-атом S), что говорит о достоверности полученных данных.
Подставив полученные значения АЯ(8) и В в уравнение (II), получим
AZ(8, =— 18 500+ 15,5r + 4,57rig/Vs. (20)
Температурную зависимость изменения изобарного потенциала реакции (9) растворения цинка в меди можно получить в предположении, что раствор является регулярным. Поэтому для реакции (9) имеем
AZ(9) = AZ(9) = АЯ(9) + 4,57Г lg Я2п, (21)
где АЯ(9) — парциальное изменение теплосодержания при растворении цинка в меди;
Nzп — атомная доля растворенного цинка в твердом растворе.
Условно предполагая, что в твердом растворе цинка в меди содержится —5% Zn и воспользовавшись значением AHZn = ~—9173 из работы [51], получим
AZ(9) = -9173 + 4,57Г lg NZn. (22)
Таким образом, определены температурные зависимости AZ^j, Z(8) и AZ(9) для взаимодействия ZnS с медью.
Подставим найденные значения в уравнение (10) и, приняв при этом Nzn — Л/'s, получим, что при Т = 1073 К атомная доля серы в растворе Ns = 0,00086, или 0,086% (ат.) S, т. е. при Т = = 1073 К термодинамически возможно такое растворение серы, которое на полтора порядка выше предела растворимости при указанной температуре (т. е. выше, чем может содержаться в насыщенном твердом растворе, находящемся в равновесии с низшим сульфидом меди). Следовательно, при взаимодействии наряду с твердым раствором, термодинамически возможно образование сульфида меди Cu2S; это означает, что термодинамический расчет по формуле
(6) дает качественный результат, а количественный результат сильно занижен.
Учтем полученные данные и произведем перерасчет, предполагая, что взаимодействие должно идти по реакции
ZnS - f 2Cu = Cu2S + IZnlcu - (23)
Естественно, что в условиях равновесия
AZ(23) = AZCUjs - f - Z[Zrl|Cu — AZZnS. (24)
В уравнении (24):
— AZzns = AZ(7), AZ[zn]Cii = AZ(9),
AZcu, s = — AZ(i3) •
Подставив найденные зависимости в уравнение (24), получим
44ЯП
lgNZn = lgNs = - ~ + 0,355lgT+ 1,735. (25)
Оценки по уравнению при Г = 1123 К дают /VZn = Ns 0,07, т. е. 7,0% (ат.) Zn или S.
Таким образом, при взаимодействии сульфида цинка с медью при температуре 850° С в меди растворяется 7% ZnS. Причем цинк полностью находится в твердом растворе с медью, образуя а-латунь с содержанием 7% Zn, а сера практически полностью находится в виде Cu2S.
Анализ формулы (25) показывает, что с повышением температуры растворимость сульфида цинка в меди увеличивается. Таким образом, для данного типа взаимодействия нельзя назвать температурный интервал или температуру начала взаимодействия по данным термодинамических расчетов. Это, очевидно, будет определяться главным образом кинетическими факторами.
В настоящее время не представляется возможным ответить на вопрос, какая минимальная степень взаимодействия необходима для получения равнопрочного с керамикой соединения и какая степень взаимодействия может быть оптимальной. Однако полученная по расчету величина 7% позволяет предположить возможность получения достаточно прочного соединения при сварке давлением с подогревом сульфида цинка с медью.
Качественная экспериментальная проверка результатов расчета производилась рентгенофазовым анализом смеси порошков сульфида цинка и меди после спекания их по режиму сварки 1. При этом наряду с исходными веществами были обнаружены фазы CuoS и CuZn. Причина некоторого несоответствия результатов рентгенофазового анализа расчетному уравнению (23) (а именно: обнаружение «лишней» фазы CuZn) была установлена при металлографическом исследовании сваренных образцов и прицельной рентгеносъемке диффузионной зоны на керамике. При сварке происходит не учитываемая уравнением (23) и не дающая вклада в образование сварного соединения диффузия ионов меди по междоузлиям (тетраэдрическим пустотам) решетки сульфида цинка с образованием твердого раствора внедрения (о чем говорит увеличение параметра кристаллической решетки сульфида цинка, определенное при послойных рентгеноструктурных исследованиях).
Поскольку растворимость с понижением температуры уменьшается, часть растворенной меди при охлаждении выделяется по границам зерен сульфида цинка в виде интерметаллида CuZn. Таким образом, результаты качественной экспериментальной проверки проведенных расчетов показали удовлетворительное совпадение.
Термодинамические расчеты и проведенные исследования позволяют констатировать, что формирование сварного соединения керамики с металлами на стадии объемного взаимодействия протекает путем растворения керамики в свариваемом с ней металле с образованием в переходной зоне разбавленных или пересыщенных твердых растворов. Растворение металла в керамике, которое может наблюдаться в некоторых системах (например, ZnS—Си), следует считать побочным процессом, не связанным с формированием сварного соединения. Но этот процесс имеет негативную сторону, а именно нарушение атомами металла присущих керамике химических связей (особенно на границах зерен) и, как следствие, снижение прочности керамики в этой зоне. Это нужно учитывать при сварке керамических материалов с металлами.