СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ

Оценка матрицы и упрочнителя в формировании свойств композита

В дисперсно-упрочненных композитах частицы начинают ока­зывать упрочняющее действие тогда, когда они ограничивают де­формацию матрицы посредством механического стеснения. Это есть функция отношения расстояния между частицами к их диаметру, а также упругих характеристик матрицы и частиц. Обычно модуль упругости композита Ек, матрица которого Ум упрочнена частица­ми V4, имеет меньшую величину, чем это следует по правилу сме­сей*:

Ek=EmVm+E4V4. (2.1)

Правило смесей (аддитивность) — свойство, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значе­ний величины его частей.

Это уравнение дает данные, выраженные в виде относительной доли предельного модуля упругости. Поскольку модули упругости упрочненного частицами композита должны удовлетворять следую­щему соотношению (равенство напряжений в компонентах):

EK=EME4/VME4+V4EM, (2.2)

всякое положительное отклонение от этого уравнения должно озна­чать стеснение матрицы, т. е. упрочняющее действие частиц.

В волокнистых композитах, как указывалось выше, включается два компонента — волокна и матрица, что дает высокую прочность на растяжение и изгиб. В этом убедимся, анализируя прочность во­локнистого композита с помощью простой модели: выделенного из композита параллелепипеда объемом, равным единице, армирован­ного волокнами, расположенными параллельно (рис. 2.2).

Содержание волокна VB и матрицы Уы дано в долях от объема композита, принятого за единицу, следовательно:

TOC o "1-5" h z Ув+Ум=и VM=-VB. (2.3)

Осевое растягивающее усилие Рк, воспринимаемое компози­том, распределяется между двумя компонентами: волокном Рв и матрицей Ри:

РК=РВ+РМ. (2.4)

Переходя к напряжениям, получим распределение напряжения в композите (при / = 1):

= °bvb + °м О - ув) • (2-5)

В пределах упругой работы материала, согласно закону Гука,

°к ~ євРвРв + емРм 0 — У в) ■ (2-6)

Композит работает, как единый материал, т. е. отсутствует про­скальзывание волокна в матрице, поэтому относительные деформа­ции композита єк, волокна єв и матрицы єм равны между собой:

£к~ £в~ £м ~ £ • (2-7)

Учитывая условие цельности композита, получим уравнение прочности волокнистого композита RK в следующей форме:

Rk=[EbVb+Em{-Vb)]s. (2.8)

Следовательно, модуль упругости композита Ек в рассмотрен­ном случае формируется по правилу смесей:

EK=EBVB+EM( -VB). (2.9)

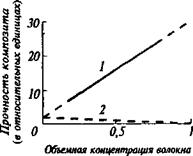
Применительно к стеклопла­стику, принимая модуль упругости стекловолокна Ев =60 ООО МПа и полимерной матрицы Ем =2000 МПа, т. е. соотношение Ев :ЕМ =30:1. Содержание волокна в стекло­пластике доводят до 80-90%, ар­мируя его не отдельными волок­нами, а стеклотканью. Из соот­ношения РВ! РМ ={EB! EM)VB /(1-FB) видно, что усилие, воспринимае­мое волокнами, увеличивается по мере увеличения содержания во­локна и его модуля упругости (рис. 2.3). Соответственно умень­шается доля нагрузки, переда­ваемой на менее прочную матрицу. Прочность волокна при растяже­нии и модуль упругости зависят от его толщины (рис. 2.4). Высоко­прочное волокцо с большим модулем упругости имеет диаметр 3- 7 мкм. Модуль упругости стеклопластика, армированного таким во­локном, составляет 18 000-35 000 МПа, он в 10-20 раз больше моду­ля упругости полимера. Следовательно, модуль упругости конструк­ционных полимерных композитов примерно такой же, как и цемент­ного бетона.

Стеклопластики с ориентированными волокнами (типа СВАМ — стекловолокнистого анизотропного материала) обладают большей прочностью — при растяжении до 1000 МПа и легкостью — плот­ность 1,8-2 г/см3. Обладая также химической стойкостью, этот мате­риал эффективен для труб, емкостей и конструкций.

Имеются материалы, модуль упругости которых на порядок вы­ше модуля упругости стекла. Проводятся работы по получению не­прерывных волокон бора, карбида кремния, углерода, а также безде­фектных кристаллов оксида алюминия (сапфира), нитрида кремния и др. Стоимость таких волокон высокая и они в первую очередь будут применяться в тех областях, где стоимость материала второстепенна. Однако можно надеяться, что со временем стоимость новых мате­риалов снизится и они будут доступными для строительной техники (как это произошло с алюминием).