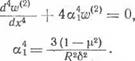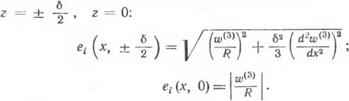СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ, ВОЗНИКАЮЩИЕ В РЕЗУЛЬТАТЕ СТЫКОВАНИЯ КРУГОВОЙ ЦИЛИНДРИЧЕСКОЙ ТРУБЫ СО СФЕРИЧЕСКИМ ДНИЩЕМ

Обозначим через R и б соответственно радиус срединной по­верхности трубы и толщину ее стенки. Примем также, что днище представляет полусферическую оболочку с радиусом срединной

тате сшивания короткой трубы III радиусом = Я (1 е(п))

с длинной круговой цилиндрической трубой II и со сферическим днищем I (рис. 49). Короткая труба будет состоять из двух ча­стей — из сферического пояса 0О ^ 0 sg л/2 и кругового цилиндра bj2, плавно переходящих друг в друга. Получающееся при этом решение пригодно также для первого способа уточнения, если под bj2 понимать расстояние от оси шва до окружности, являющейся средней между окружностями Тк И Ту. Примем также, что средняя толщина трубы III мало отличается от б, так что можно принять б3 = б.

Ограничимся случаем, когда рассматриваемые оболочки яв­ляются тонкими. При этом в зависимости от величины начальной равномерной температуры свариваемых оболочек, т. е. в зависи­мости от величины а (Тк — Т0) составная оболочка может на­ходиться или в чисто упругом, или в упруго-пластическом состоянии.

Рассмотрим сначала упругое состояние составной оболочки. Для составления условий сшивания и удовлетворения этим усло­виям найдем деформации, усилия и моменты рассматриваемых оболочек.

Упругое состояние оболочки

Днище I. Деформации, усилия и моменты этой оболочки определяются формулами (8.110), которые при 0 = 0О ((5=0) дадут:

Ш(1) (0о) = -^-с}1);

*(1> <е°)=~4г (с{1)+с*1));

мі11 (Єь) = - сС^;

Труба II. Радиальные .смещения точек срединной поверх­ности этой оболочки будут удовлетворять [120] дифференциаль­ному уравнению:

деформаций, а также усилия и момента соответственно будем иметь:

SHAPE * MERGEFORMAT

w' ‘ (л:) = [Cl2) cos аХ + Ср sin а,х] ё

dx = — CLi [(с{2) — СР) cos aiX + (Ci2) + Ср) sin оце] е~аіХ;

Mp = —D

и принято, что радиальное смещение ш(2) (х) положительно в на­правлении внутрь трубы.

Труба III. Как было указано выше, труба III будет состоять

из сферического пояса 0о^0=^-у - и кругового цилиндра 0^

^ х ^ Деформации, усилия и моменты сферического пояса

определятся формулами (8.114), которые в этом случае перепишем в виде:

Ш<3) = [(cff COS Р - ейР Sin р) е~р +

+ (Cfi)cosp+Cf1)sinp)ep];

®и> =ЙУт|11<С" + Сй> )cos р + (С! ї> — сй‘) sm Р] е - - [(СІ?> - й?) sin р + (C3S) + ci?>) cos р] Єр); Л1І3) = — с [(СІ?» cos Р + С[?> sin Р) <ГР +

+ (СІ?» cos р — df Sinp)ep];

1/х

Q<3> = _ L^- І [(сі? - Cg>) cos P - (сі?» + сі?») sin Р X e-p + [(Сі?» - СІ?>) cos p - (Cif + Ci?») sin p] ep|,

где

Р = /-£<е-в.).

Отсюда при 0 = 0О (р = 0) получим:

(3> (Єо) = 4-(сі?+сі?));

Е 6

0(Г1) (00) = Ж^ ^ - Сі?);

Мі3» (0О) = — с (СІ?» + СІ?»);

/ гДЗ) /-'(3) і /-ДЗ) г(3)

TOC o "1-5" h z /0(3) /о 1/ с 11 21 ^ °41 Ь31

Qy = — у ~2R '

зт

Те же формулы (8.133) при 0 = , т. е.

при р = р, = (/(;■(-2-------------------- 90). дадут:

“W ("Г) ” Ж КС“ с«Р, - Сй’ sin р.) е-*- + + (Сз?» cos Pi Т СІ?» sin Pi) вРі];

(іґ) “ Ж V-WІ + Ci?)cosp, +

+ (Сі?) - СІ?)) sin Pj] <Гр‘ - [(df + Сі?)) cos РН - + (сі?) —eg)) Sin Pi] ер1}; Mi3» (-J-) = - с [(Сі?» cos р1 + С}?» sin р,) е~р‘ + + (СІ?) cosPi —C3?»sinPi)ePl];

(^“-V^IIW-Cfficosp,- -(Ci? + tS,)slnp,].-fc +

+.[(ci?> - Ci?)) cos Pi - (Ci?) + Ci?)) sin Pj }.

16 г. Б. Талыпов

Деформации, изгибающий момент и перерезывающая сила второй части трубы определятся путем решения дифференциального урав­нения (8.130), и для них при этом получим:

ш(3) (х) = (С(р cos ахх + С22 sin ахх) еа, х +

4“ (ср COS (Х{Х -| С42' sin ex 1-^) е <x, Aj

dW<dx(X) = “1Ы + СР) COS аХ + (Ср - Ср) Sin сц*] X

X еа'Х — ССі[(Сз2* — Ср) COS <Xix -)- (ср - f - СІ3*) Sin Uix] e a'x',

Mp (x) = — 2a 1D (Cp cos at* — Cp sin axx) ea‘x —

— 2a[D (Cp sin aX — Cp cos ape) e~ai*',

Qp (jc) = — 2aD I (CP — Cl3)) cos a,* — -(Cf2)+C^))sina1*]e“‘j: +

-f 2a? D [(Cg> - CP) sin ape - (CP + CP) cos axx <f

Последние~при x = 0 и х = - у - соответственно дадут:

ш(3) (0) = c[f + с£3);

dw<3>

== а1 У12 “1 '-'22 - ^32--- 1^42 ),

x=G

МР (0) = - 2aD (СР - СРУ,

- «і [W - СР) cos г) + (С^ + СР) sin ті] в"71; М. Р — — 2аіD (Ср cos 11 — СР sin tj] еп — — 2а? D (Ср sin ті — Ср cos т]) е~

QP (4) = — 2аЇВ [(СР - СР) cos tj -

-да+С^))5іпті]вт1 +

+ 2аD [(СР - СР) sin т) - (СР + СР) cos т,| е~

В сечении 6 =-^- (х = 0) трубы III должна быть обеспечена не­прерывность деформаций до, до', изгибающего момента и перере­зывающей силы. При этом условиями сшивания трубы / с тру­бой III, указанными условиями непрерывности, а также усло­виями сшивания трубы II с трубой III соответственно будут:

Эти условия дадут следующую систему алгебраических уравнений для определения постоянных интегрирования:

—ср> + с{?>+сй> = Гбсс (г* - Го);

A - rG) I /-(3) W3) г(3)

Ol 02 Оц ' '-'21 — Ьзі --------------------------------------------- 0,41

/о(1> W3) L/o(3).

0-2 = 0,21 ( 041 J

г*( 1) /о(1)_/о(3) Г( 3) ,/о(3) /о(З).

Ог Oi —Оц 021 (“041 —"Оз1,

> /о(3)

' h 041 '

-щ |.(Сп> cos Pi — С|3) sin Pi) е

. /-.ізі . п вл

+ (eg cos Pi + Cg> Sin Pi) ер‘] = сі? - С$;

Так как полуширина зоны шва, где в результате сварки механи­ческие свойства основного металла получают необратимые изме­нения, мала, то для тонких оболочек с достаточной точностью

можно принять sin • Тогда получим, что

р! 1] с той же степенью точности. При этих условиях решением

системы (8.140) будет:

СІ1» =да?» ~Е6а(Тк

-То);

Г<1> — г*(3)-

— О41 >

С(12» = ср + 4 (Тк - Т0) в’1 cos 4;

СР = СР 4- 4-Ra (Тк - То) в1» sin 4;

С(ії = ±-ЕЬа(Тк — ТоУ,

СІЇ = 0;

Сії = - Leба (Тк - То) е“2ї1 cos 2ч;

Сі? = ЕЬа (Тк — То) «Г*4 sin 2т];

Сії» = -~Ra(TK - Т0)costj; (8Л41)

Сі» =------------- y Ra(TK— Т()) є-*1 sin rj;

Сі» =-------------- L Яа (Т* - Га) е 11 cos tj;

Сії» = - y Ro. (Тк - Т0) sin т).

При найденных значениях постоянных интегрирования (8.141) деформации, усилия и моменты в отдельных частях составной оболочки и, следовательно, приближенные значения деформаций,

усилий и моментов, вызванных стыкованием цилиндрической трубы со сферическим днищем, определятся формулами (8.110),

(8.130) , (8.133), (8.136).

, Далее следует отметить, что так как длина трубы III мала по сравнению с ее радиусом, то можно добиться некоторого упро­щения задачи, заменив трубу III сферическим поясом или кру­говой цилиндрической трубой. В случае тонких оболочек такая замена не может привести к большой погрешности.

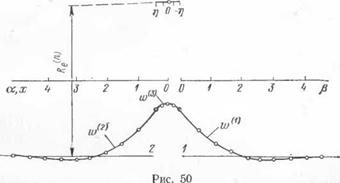
, Далее сравнение величин, w(2) , ы»(3) показывает, что наи­большее радиальное смещение оболочки III значительно больше, чем максимальные радиальные смещения оболочек I и II. Для иллюстрации на рис. 50 показана образующая составной оболочки после сшивания. Там же прямыми линиями /, 2 и 3 показаны положения образующих оболочек /, II, III до сшивания. Рас­четы проведены для R — 50 см, б = 1 см, = 4 см, р, = 0,3. Непосредственно видно, что в данном случае Wmах (штк) состав­ляет примерно Wmlx. Выше, при решении задачи было принято,

что оболочки /, II, III имеют одну и ту же постоянную толщину б, т. е. не учитывалось усиление оболочки III от наплавленного металла. Это усиление можно учесть путем введения приведенной толщины б j оболочки III, где б ] > б. Эта задача может быть ре­шена аналогичным образом, причем учет усиления оболочки III приведет к увеличению ьг/(1) (ьу(2)) и к уменьшению щ<3).

Аналогично может быть решена задача определения сварочных деформаций (напряжений), вызванных приваркой днища, имею­щего форму сегмента. Эта задача сведется к определению дефор­маций (напряжений) составной оболочки, получающейся в ре­зультате сшивания короткой оболочки III с сегментом и с круго­вой цилиндрической оболочкой. При этом оболочка III будет состоять из двух частей — из сферического пояса и круговой ци­линдрической трубы, образующие которых пересекаются под известным углом.

Упруго-пластическое состояние оболочки

Как показано, если пренебречь усилением зоны шва от на­плавленного металла и принять, что оболочки I, II, III имеют одну и ту же толщину, то начальная разница между их радиусами при сшивании компенсируется главным образом за счет короткой трубы III. В этом случае естественно предположить, что при уве­личении параметра а (Тк — Т0), т. е. при понижении начальной равномерной температуры стыкуемых оболочек в сторону нор-_ мальной температуры, в пластическое состояние в первую очередь перейдет короткая труба III, а смежные оболочки / и II оста­нутся в упругом состоянии. Тогда для оболочек / и II останутся справедливыми решения, полученные ранее. Короткая труба III, как показано выше, в случае тонких оболочек без ущерба для точ­ности может быть заменена круговой цилиндрической трубой. Осесимметричные упруго-пластические деформации круговой ци­линдрической трубы достаточно подробно исследованы А. А. Иль­юшиным [44], так что здесь не могут возникнуть какие-либо принципиальные трудности. В каждом конкретном случае ис­пользование его метода упругих решений потребует лишь прове­дения необходимой вычислительной работы. Вместе с тем, учиты­вая, что при применяемых на практике режимах сварки, осо­бенно при автоматической сварке, ширина зоны интенсивного нагрева в предельном состоянии весьма ограничена, наравне с приемом, использованным в п. 44, можно указать другой прн -

ближенный прием определения упруго-пластического состояния составной оболочки (п. 38, 43).

Действительно, если начало координат поместить в точке срединной поверхности, то интенсивность деформаций

e‘=vrV т(т) + 2 ЬИ

Имея в виду (8.137), для и по формулам (8.136)

получим:

а>(3) =-------- — Ra (Тк — Г0) [cos (ті — ахх) - j - е~2а'х cos (ті - f «і*)]’,

= — Ra'la (Тк — Го) [sin (ті — аД') - f e~2а‘* sin (ті - f a^)].

Отсюда ясно, что при достаточно малых т], где для тонких стальных (р = 0,3) оболочек

4______________

аА ^3(1 —p2)6t 1,28 1^5 bj

11 ~ 2 2 у R6 ~ R ’

d2w{3)

wi3) и dx2 при х = 0 будут мало отличаться от их значений

при х = - у. Для таких малых ті величины 0/(-у» - у-) и е,- (0,0) будут близки друг к другу. Например, даже при 6, = 0,17? вели­чина ± - у) больше е,- (0,0) всего на 10%. Но, как ука­

зано выше, на практике величина Ь1 весьма ограничена. Имея в виду случаи, когда bt <£ R, для простоты можно принять, что оболочка III целиком перейдет в пластическое состояние при том значении ер) параметра а (Тк — Го), которое определится из условия

е!'* (о, о) = = еи.

Ввиду малости рассматриваемых нами деформаций, можно принять, что металл трубы III следует схеме идеальной теку-

247

чести. Тогда при последующем увеличении основного параметра от ер) (0,0) до его нормального значения деформированные (на­пряженные) состояния оболочек lull останутся неизменными и определятся формулами (8.129), (8.131) при том же значении еТ (0,0) параметра а (Тк— Т0).