СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
НЕКОТОРЫЕ ЗАДАЧИ 0 СВАРОЧНЫХ ДЕФОРМАЦИЯХ И НАПРЯЖЕНИЯХ ТОНКОЙ СФЕРИЧЕСКОЙ ОБОЛОЧКИ
Деформации и напряжения сферической оболочки, возникающие в результате вварки заплатки сферической формы
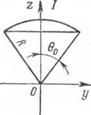
Обозначим через R начальные радиусы оболочки и заплатки и примем, что они изготовлены из стали одной марки. При этом здесь и в последующем будем рассматривать геометрически линейную задачу, т. е. случай, когда стальная оболочка не является гибкой, а имеет достаточную жесткость. При решении этой задачи используем первый способ уточнения (п.31). Пусть 0О и 0j определяют ЛИНИИ, являющиеся средними между ЛИНИЯМИ Тк И Ту (п. 31) предельного состояния нагрева соответственно справа и слева от оси шва, накладываемого вдоль замкнутой параллели 0. Тогда в соответствии с основной гипотезой и принятым способом уточнения сферический пояс 0О ^ 0 sg: 01 при сварке получит активную пластическую деформацию сжатия а (Тк — Т0). Другими словами, если все элементы, находящиеся внутри этого пояса, освобождать от остальной оболочки в моменты, когда температура их остывания достигнет значения Тк, то после прохождения электрода по замкнутой параллели и остывания до начальной температуры Т0 все эти элементы будут образовывать сферический пояс III радиуса = R [1 —а (Тк— То)]. При этих условиях задача определения приближенных значений сварочных деформаций и
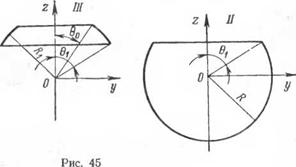
напряжений, возникающих в точках исходной оболочки в результате сварки сферической заплатки, сведется к определению деформаций и напряжений составной оболочки, получающейся путем сшивания сферического пояса III (рис. 45) с сегментами I и II [8]. При этом примем, что заплатка и сферическая оболочка имеют одну И ту же толщину, Т. е. б 2 = б!, а пояс III будет иметь переменную толщину, среднее значение которой обозначим через б3. Ограничимся случаем, когда составная оболочка после сшивания оказывается в упруго-деформированном состоянии.
|
|
|
|
Подлежащие сшиванию части /, II, III составной оболочки свободны от внешних поверхностных сил и для каждой из них можем использовать известные выражения [81 ] радиальных смещений w, поворотов v, а также усилий и моментов.
Сегмент /:
о>(1) = (сР cos Р — C21}sin Р)е~р);
#(,,= ~жУж [tf’+Ci4) cos Р + (CP-CP)s іпр]<Гр;
|
(8.110) |
7ІЧ =~Y-Jb ctge [(CP-CP) cos p+(c{1} + CP)Sin p]e-p;
Np = TP tg0;
T{P = (CP cos P — C{P sin p) <ГР;
wO)
0(1> = _*_■ sin 0 ’
МР = — Сг{С! р cos p + C^slnP) e~p,
где
Ci =
/12(1
М{1) (Оо) = - СхС^;
|
(8.111) |
Сегмент II:
„(2)
w'-1 = (cl2) cos Р—d2)sin Р)е~р;
»<2'=жКЇ[(с''+с“,)с“(,+
+ (Ct2)-d2))sinp]e'p;
|
(8.112) |
7?> = ]Л§- ctg 0 [(Cf >-Ci2)) cos p + + (Ci2)+Cf))sinp]e-p;
"!!,=K¥[w,-^,)c°sp+
+ (Ci2> + C42>)Slnp]e-<!;
m(2)
0<2> — 1— - 4y — sin e ’
7f > = (C(i2) cos p — Cfsin p) e-p;
|
где |
M[2) = — Ci (CP cos p + Cl2) sin p) e-p,
р=/Зг<е^е->-
Последние на линии сшивания 0 = 6j дадут:
|
9 |
|
,(2) |
|
W |
|
(0.>=жсР; |
в«(е1) = - ЛгрЛ-^г(с! аЧсІ!’);
м‘2) (0і) = —СіС22);
Г>(2) (0 ) - - Т / с1 С22) _ С12>
Qi/ *”1/ у ад-—Ее;—•
ш<3) = - J - [(Сі3) cos р — CP sin р) .Ні +
+ (CP cos р + CP sin Р) ер];
®,’’ = і>/ЇІ[(сі”+с“>С0!іі,+
+ (Сі® — С5!>) sin р] е~*
- [(сГ + cf) cos р + (ср + сР) Sin Р] ер); Тр = ~У ^f-ctge {[(сі3) - С$3)) C0SP -
-(Ci3) + d3))sinpKP +
|
(8.114) |
+ [(СР - СР) cos р - (CP + CP) sin pj еР); NP = TP tg 0;
Tj8» = (Сі3) cos р — CP sin р) е' р - I - + (CP cosP + Cf' sinp)ep; l/Ь.
«“ = - T5^([(C|S’-C“)cosP- -(CP + C?»)slnp]£-?i +
+ [{Сі** - Cf) cosp - (Cf + Cf’)sln p j; МР = —C3 [(c!3) cos P + Cp Sin P) e'p +
+ (Cfcosp-C^sinp)ceJf
е=1/5г<е.-0">-
На линиях сшивания 0 = 0О, 0 = 0г получим: м)(3) (0О) = - щ - (C(i3) + Сз3));
о<з> (0О)=(ср) + ср) “ cf) “ cf)):
мі3) (0о) = —Сз (с4в> — Сі3>);
.... . , г~сг с<3) — ср і cf> — cp
<т(в.=-у^——W——;
to™ (їїі) = У'- [(Ci*’cosPi - Сіа> sm (і,)<ГРі + £03
+ (CS8)cospi + Ci8)sinftl)ep‘];
|
(8.115) |
§ (3) (0і)=ж {[(сР>+ср))cos Рі +
+ (Cf>-C|3))slnp1]e-p*- - I(Cf + Cf) cos P, + (CP - CP) Sin Px]/‘};
Mi3) (0,) = —Сз [(Cf11 cos Pi + CP sin pt) e~Pl + + (Cf )cos Pi — Cp sin Pi) ePl;
|
£a_ 2R |
V
^ (e>) = “ 4г§г {[(c<l3) “ cp>) cos Pl “
— (Ci8) + CS8))slnPi]e-Pl +
+ [(ci3> - CP) cos p; - (CP + CP) Sin P.]
|
где |
Постоянные интегрирования определятся из условий сшивания:
- ^(1) (60) + w™ (0О) = Ra (Тк - 70);
^(1)(0о) = ^(3)(0в);
М<1>(0О) = УИ<3>(0О);
, Qp (в0) = ^3)(Є0);
- ш<2> (0,) + ш<3> (0j) = tfa (Тк - Тоу,
д<2)(01) = '&(3)(Єі);
M<2)(01) = Mf)(01);
(ЄЛ) = <?і,3)(Єа).
Условия сшивания (8.116), если иметь в виду соотношения (8.111),
(8.113) , (8.115), дадут следующую систему уравнений для определения постоянных интегрирования:
- нгс™ + Ж (с" + Ч») = R“ <г« - т«);
-ж/ЗГ(с1,|+ч1>)=
= НГ^ЇІГ (Ч31 + Ч*> - Cf. - С»>);
С, ф = С,(С?>4-Ср>);
іГсГсі”~Ч3) + с{»>-с|»
Г 2R sin 60 21? sin 0О ’
- жс12) + -&г [(с53) cos - с23) sin е ~Pl +
+ (ср cos + q»> sin Pt) eP.] = Ra (TK - T0);
жУъ(с?'+с?')~ткУ1ъгІКЧ3’+ <8JI71
+ q3>) cosp! - f (C<3) — Cp) sin P,] e-ь —
- [(ф + Cp) cosp, + (Cp - CP) sin px] eP.};
qq2> = c3[(q3> cos & + q3> sm px) *-p* + + (q3> COS Pi — ср sin Pi) eP>];
,/ЬГ
/■ с, C<2> - ср _ _ X _2g_ j r/q3) _ C(3) 4 cos Bi _
V W ііїГе^ sin e, ' ^ 1 2 >
- (q3> + cp) sin р/j в-». + |(q3) — q3)) cos px —
— (ср - r q3)) sin Px] eP*).
Если ввести обозначения:
|
(8.118) |
‘--■-’(ІГ+Ш’;
“>=ч-2аг+ш!;
q1' = - ~ (-^)1/2 [4- c(i3) - ьсР -
-±(а + аОСр+ЪС?>]; (8И9)
с‘«= -4-(|-)'/2 [-^<з) +4-(°-ь«і)Ф+
+ М:й_|(й_Иі)с(3)] .
При этом из первого и третьего уравнений системы (8.117) получим:
с<»> = еь (Ау/2^а(гк- 70) - Aq3. _2 (A)1,2ACf); q»> = ЕЬ, (А)1/2А а {Тк - т0) - 2 (Ау2 А С<3) — Aqs),
(8.120)
|
(8.121) |
где обозначено:
|
o2 |
= 1 — 2 |
(t |
у/2 |
+ ( |
в, 2 ь) |
1 * |
|
a3 |
= 1 + 2 |
(t |
у/2 |
+( |
6i 2 в./ |
У |
|
'’■=2i |
At) |
-( |
Є3 «і |
г |
Г1- |
(t)1> |
|
<>.=41 |
At) |
+ ( |
6з бі |
г |
А |
(t)4]= |
|
*+t) |
+ ( |
V А |
п |
1 + |
(t)T- |
Аналогичным образом из уравнений шесть и восемь системы (8.117) будем иметь:
cl2)=4 ci3> [(i)3/W + Sin Pi) +
+ (^")1/2 (C0SP1 — smpjje-p* +
+ 4- CS3) [ ( A yy2 (cos — sin Pi) —
- (l-y W + sinPi)] е-P.—
~тс*3) f(^-)3/2(C0SPi—slnPi)+
+ (-^-)1/2 (C0SPl + sin Pi)] ePl —
— -1 Cf> [(-|-)8/2 (cospx + sin Pi) - - (-|-)1/2(cosPi — SinPj)] eP.;
CP = ± C[3> [(-|l)3/2(cosPi + sin Pi) -
_ (lr)1/2(C0SpJ — SinPl)] e_Pl + (8.122)
+ ^23) [(-|-)3/2 (cos Pi — sinpi) - f + (-|f)1/2(cosPi + sin Pi)] e-h —
- Сз3} [(-|)3/2(cosPi-sinPi) -
“ (~t")1/2(cospl + sinpl)]epI -
— -Y cfi (cosPi + sinPi) +
+ (-^)V2(cosPi-sinP1)] eP*.
Если теперь подставить (8.120) и (8.122) в пятое и седьмое уравнения системы (8.117), то получим:
Сз3) | [^-у - (a cos Pi — sin Pi) —
— 2 )3/2 -y (b cos Pi + a sin Pi)] e - P. +
+ [Пі COS Pi -|- b Sin Pj ep. ] +
+ Cf > {[2 (-|-)1'24(GCOSpi-fe sin Pi) —
— -^-(fcCOSPi - f GSin Pi)]e-P. +
+ [—& COS Pi - f - Cl Sin Pi] eP.] =
= ЕЬг (^-)1/2{2 - f [7г (° cos px — b sin Pi) — --^(bcospj-f asinPi)] e P* j a(TK — Toy, Cl3) j [-7- (b cos px — g2 sin pi) —
— 2 (-^-)3/2 7 cos Pi + sin Pi)] e ” Pl +
|
(8.123) |
-j - [b cos Px 4- g3 sin Pi] ep‘] 4- + Cf> j [2 (-^-)1/2 (b COS P, — Go Sin Pi) —
Y (G2COSPi + b Sin Pi)] e - P* —
— [GgCOSPi — fcsinPi]eP>] =
= £61 (-|^)1/2 [-7- Ф cos Pi — g2 sin p,) —
— Y (dz cos Pi + fcsin Pi)] e P. -
Последние дадут:
Cf =
£6X (-7-),/2 [MD —MD + (MC —ЛІ'С)е-2Р‘] a(T„ —Г0)
Л D — AD + ВС — ВС + (АС— АС) е-2р‘ +
|
(8.124) |
+ (£D — І£>)е2Р‘
Cf> =
£61 (тг),/2 — &М + (AM - AM) е-2р‘] а (Г« — Го)
Л£ — Л£> + ВС — ВС + (АС — АС) е 2Р‘ + ’
|
где обозначено: |
+ (BD-BD)e2^1
A — (a cos Pi — b sin pi)
— 2 U ~ (b cos Pi + a sin Pi); В = Gi cos Pi + b sin Pi;
|
_?JL с |
|
A В = b cos pj - f - a3 sin Px; h с D = —as cos Pj + a sin PiJ M = - y. (6 cos Pi — a2 sin Pj) - |
|
~ (b cos p! — a2 sin Pj) - y - (g2 cos pj + |
|
(8.125) |
|
= —о cos рг|-йі sin p,; M = 2e&' + — (a cos Px — b sin Pi) С b — — (6 cos Px-f asin Pi); — a2 sin b sin pt); |
|
'|j-) /! (b cos Pi — a2 sin Pi) - - y - (a2 cos Pj 4- fcsinPi); |
|
(fecos^ -(-я sin px); - b cos Pi h °isin Pi ; |
|
L - - (02 COS Pj + b sin p,). |
|
D: |
|
|
Зная постоянные С|3), СІ3>, по формулам (8.119), (8.120), (8.122) можно определить все остальные постоянные интегрирования. При этом деформации, усилия и моменты составной оболочки определятся по формулам (8.110), (8.112) и (8.114).
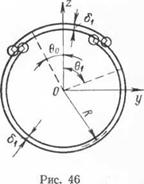
Полученное здесь решение равным образом может быть использовано для исследования деформаций и напряжений в двух других случаях, а именно, в случае подогрева сферической оболочки вдоль замкнутой параллели или же наложения тонкого валика на поверхность сферической оболочки вдоль этой параллели, а также в определенных случаях приварки внахлестку заплатки сферической формы к сферической оболочке (рис. 46).
Подогрев или наплавка тонкого валика вдоль замкнутой параллели
В этом случае имеем 61 = б2 = б3 = 6. При этом условии формулы (8.118), (8.121) и (8.125) дадут:
TOC o "1-5" h z ао — а2 — 0; «і = а3 = 4; b = Ь± = Ь2 = 0; с = 8;
А = А = 0; В = 4 cos Pj ; В = 4 sin р х;
С = С = 0; D = 4 sin р j; D — —4 cos р х;
М = 2еР>; М = О,
а по формулам (8.119), (8.120), (8.122) и (8.124) для постоянных интегрирования получим:
с[" = - 4- Е8 (1 - е"9, cos РО а (Г, - Го);
= - і - £бЄ-Ріа (Тк - Т0) sin pi;
Cf > = -±Е6( 1 - <ГР‘ cos рО а (Г, - Го);
С<2) = 4-£бЄ-р‘а (Гк - Го) sin Рь
( (о. 1 zb)
с<3) =±Е6а(Тк-Т0);
С?> = 0;
Cf = |£&Л(ГК-Г0) cos р,;
Cf = - ІДбвЛх (Гк - Го) sin рь
Деформации, усилия и моменты составной оболочки найдутся по тем же формулам (8.110), (8.112) и (8.114). Например, если возьмем случай наплавки тонкого валика по диаметральному сечению, для сегмента II (рис. 45) будем иметь:
а>(2) = ~y Ra (Гк — Г0) [а - (P+Pi) cos (Р + Pi)— е-р cos Р];
= - Т У-WEba(T«-To)x
X |е_(Р+Р*> [sm (Р + Pi) — cos (Р + PJ] — g-P (sin р — cos Р)} ctgO; тр - - Legа (Гк — Го) [ё~(P+Pl) cos (Р + Р0 - е~р cos р],
где
р=/|г(е-е1).
|
Аналогично для пояса III получим: = ~ Ra(TK — Tu) [е-Р cos р + еР-Р* cos (Р — Р^]; |
|
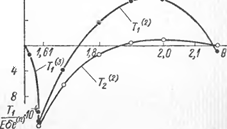
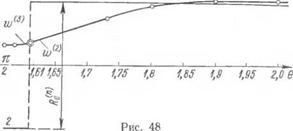
.y^ESa{TK-T0): t—ri/ , sin (P Pi)] б P Pi = yr-|r(0i-eo); Р = |А§-<в-во). Так как ширина шва вместе с шириной зоны термического влияния мала по сравнению с Я, а углы 0О и 0! близки к то, как нетрудно убедиться, при больших R наибольшие поперечные усилия Ті в зоне шва будут составлять j ших продольных усилий 7Y продольных и поперечных R № — 50, показывающие, что ^ в этом случае наибольшие ^ поперечные усилия состав- Отметим также, что продоль- в рассматриваемом случае Пс тому же закону в этой смещения w. На рис. 48 сплошными линиями 2 и 1 указаны обра- |
|
ыДЗ) |
|
1_ 2 |
|
7?> |
|
2 f 2R v к v' '' X {eP-Pi [cos (Р — рх) + sin (P — px)] — e~P (cos p — sin P)} ctg 0; T,(,3) — _L FSr, IT — ТЛ Г/>-Р rnc R _U /,P-P* COS (p — Pi)], |
|
где |
|
Рис. 47 |
|
|
Приварка внахлестку сферической заплатки
Полученное выше решение применимо также к исследованию деформаций и напряжений сферической оболочки, вызываемых приваркой внахлестку сферической заплатки, в том случае, когда температурные поля внутреннего и наружного швов (см. рис. 46) тар перекрывают друг друга, что в предельном состоянии нагрева дл я каждого из этих швов средняя между этими швами параллель совпадает со средней между кривыми Тк и Ту кривой, или же когда эта параллель окажется ближе к данному шву, чем указанная для него кривая. Если 0О и 0j определяют параллели, совпадающие соответственно со средними между линиями Тк и Т,,
|
/
|
кривыми с наружных сторон верхнего и нижнего швов (см. рис. 46), то задача определения приближенных значений сварочных деформаций и напряжений сферической оболочки, вызванных приваркой внахлестку заплатки сферической формы, сведется к определению деформаций и напряжений составной оболочки, получающейся путем сшивания сферического пояса III радиусом R3 = R - f 63/2 с сегментом / радиусом Ri = R - 6 , и с сегментом II радиусом R. Пусть оболочка и заплатка имеют одну и ту же толщину, так чтР б2 = 6j. Среднюю толщину пояса III обозначим через 63. При принятых условиях деформации усилия и моменты в частях R II, III составной оболочки после сшивания определятся соответственно формулами (8.110), (8.112) и (8.118), где для сегмента / вместо R необходимо подставить R - J - 6 х, а для пояса III—R -|-
Постоянные интегрирования найдутся из условий сшивания
(8.116) , которые дадут систему уравнений, аналогичную системе
(8.117) . Если в этой системе пренебречь отношением - п по сравнению с единицей, как это принято в теории тонких оболочек, то придем в точности к системе (8.117). Таким образом, в этом случае постоянные интегрирования определяются полученными выше формулами (8.119), (8.120), (8.122) и (8.123), а деформации, усилия и моменты составной оболочки — формулами (8.110), (8.112) и
(8.114).
Деформации и напряжения сферической оболочки в результате мощного сосредоточенного нагрева (горячая правка)
| Местный сосредоточенный нагрев нередко применяется как технологическая операция для правки бухтин, возникающих из-за потери устойчивости начальной формы в результате сварки. Во всех таких случаях наравне с задачей определения деформаций и напряжений, возникающих после правки бухтин путем мощного местного нагрева, представляет значительный практический интерес количественная оценка степени осаживания бухтины после такого нагрева. Форма поверхности выпучивания (бухтины) может быть различной. Рассмотрим случай, когда форма поверхности выпучивания является сферической с радиусом R. Так как речь идет о резко сосредоточенном местном нагреве, когда вместе с удалением от зоны нагрева деформации и напряжения уменьшаются весьма быстро, вместо части сферической поверхности, переходящей вместе с удалением от зоны нагрева в исходную поверхность (или плоскость), возьмем негибкую стальную замкнутую сферическую поверхность такого достаточно большого радиуса R, что зона интенсивного нагрева по форме будет весьма близка к плоскости. Пусть 0О определяет параллель, являющуюся средней между кривыми Тк и Ту предельного состояния нагрева, где Г s== Т0 при 0 0о. Используем первый способ уточнения,
заключающийся в том, что в области, где в предельном состоянии нагрева Т ==£; Тк, действительную температурную кривую Т (0) заменяем ступенчатой прямой. Тогда в соответствии с основной гипотезой и этим способом уточнения можем принять, что весь сегмент, определенный углом 0О, в предельном состоянии нагрева получает активную пластическую деформацию сжатия а (Тк — — Т0). Другими словами, если каждый элемент, содержащийся в этом сегменте, отделить от остальной оболочки в момент, когда температура его остывания достигает значения Тк, то к моменту своего полного остывания до начальной температуры Т0 он получит относительное уменьшение своих размеров на величину а (Тк — Т0). Освобождая таким же образом от оболочки все другие элементы, содержащиеся внутри области 0 ^ 0О, получим сегмент /, радиус R1 которого меньше радиуса оболочки R на величину Ra (Тк— 7"0). При этих условиях Приближенные значения деформаций и напряжений в точках исходной сферической оболочки, возникающие в результате мощного местного нагрева и остывания, можно определить как деформации и напряжения составной оболочки, получающейся путем сшивания сегментов / и 11 одинаковой толщины б (см. рис. 45) при 0, = 0О. При этом в зависимости от величины основного параметра а (Тк — Т0) и механических свойств металла сегментов I к II составная оболочка после сшивания может оказаться или в чисто упругом деформированном состоянии, или в упруго-пластическом. Рассмотрим
случай, когда составная оболочка оказывается в упругом состоянии. Эти два сегмента / и II, подлежащие сшиванию, будут свободны от поверхностных нагрузок и для каждого из них, рассматривая их как тонкие сферические оболочки, мы можем использовать известные выражения радиального смещения w [81], поворота Ф, а также изгибающего момента и усилий.
Сегмент /:
= (ci1» cos р - С? Sin р) «г*>;
= —-&■ Уъ [(СІ” +Йц)а*1> +
|
(8.127) |
+ (ci^-c^sinp]^; т[ц = - У^ ctge [(СІ1» - СІ1») cosp +
-ИсГЧсП sin р]е-р;
Ni] — TiX)tg Є;
ТІ1» = (СІ1» cos p — СІ1» sin p)e~?‘
Mi1» = — с (Cl1» cos p + Ci1» sin p) <rp;
ДгО)
0(1) __ W1
~ sin e *
где
|
У 12 (1 — fi!) |
P = jA§<e„-0).
Сегмент //:
-J^- (Ci2) cos p - Ci2) sin p) e-p;
®в=ж /ll(cf’+cr>)coSp +
+ (ci2)-ci2)) sin p] *rp;
7f» = ctgO f(cf»- СІ2») cos P +
+ (Ci2,+Ci2))sinp] e 3;
Mi2» = ГІ2» tg 0;
7І2» = (C{2) cos p — Ci2) sin p) e~e; Mi2» = —с (СІ2) cos p - f C{2> sin p) e
|
w |
|
(8.128) |
(2)
-P.
P = Ki(0-e«>-
Эти соотношения на линии сшивания (0 = 0О, р = 0) дадут:
“'(1)(ео) = 4-С'1);
^(1) (Эо) = - ~ V І (с^ + С”>);
|
(0О) = —сС(1)- |
|
2 > — Г(1) с о2 ьі 2R sin 0О |
О‘1)(0о) = - уГ-
ш(2)(0о) = ^-С{2);
^(ec) = il^(cf) + d2,);
Mi2)(0o) = - cCf;
|
Q<2) (00) = ]/, |
с<2>-с<2>
2/? sin 0О
Постоянные интегрирования найдутся из условий сшивания: - и*» (0О) + ш<2> (0О) = Ра (Тк - Т„);
0<Ч (0О) = (0О);
м!» (0о) = м2) (0о);
Q</> (Оо) = Qf (fib),
которые дадут систему алгебраических уравнений:
Ci2) = £6a (Т.-Го);
— (cix> + d1}) = с{2) + с22);
с^> = сГ;
— (с$ч — cl1’) = cf — ci2).
Решение этой системы будет:
СІ1» =------ y Е&а (Тк — Т0);
С?] = 0;
С[2) = ±-Е8а(Тк-Т0у,
При этих значениях постоянных интегрирования деформации, усилия и изгибающие моменты в точках составной оболочки найдутся по формулам (8.127), (8.128). Например, для. радиальных ■смещений имеем:
orfU = l2-Ra(TK-T())e Р cos Р;
t0(2) = -L {Тк — То) е Р cos р.
Отсюда ясно, что при правке бухтин, когда нагреву подвергается весьма ограниченная зона 0О ->0, выпрямление может иметь порядок, не превосходящий величины Ra (Тк—Т0).
 СВАРОЧНЫХ ДЕФОРМАЦИЯХ И НАПРЯЖЕНИЯХ ТОНКОЙ СФЕРИЧЕСКОЙ ОБОЛОЧКИ" width="144" height="184 "/>
СВАРОЧНЫХ ДЕФОРМАЦИЯХ И НАПРЯЖЕНИЯХ ТОНКОЙ СФЕРИЧЕСКОЙ ОБОЛОЧКИ" width="144" height="184 "/>