СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ В ТОЧКАХ ЛИСТА, ВОЗНИКАЮЩИЕ В РЕЗУЛЬТАТЕ НАПЛАВКИ НА ЕГО ПОВЕРХНОСТЬ ДВУСТОРОННЕГО КРУГОВОГО ВАЛИКА (32j
Теоретическое решение
С известным основанием к этой задаче может быть отнесена задача определения сварочных деформаций (напряжений) в точках листа, возникающих в результате вварки заплатки круговой формы или в результате приварки тонкостенной трубы к плоскому листу. Возьмем круговой диск конечного радиуса R и найдем его деформации и напряжения, вызванные наплавкой двустороннего валика вдоль некоторой внутренней окружности радиусом R0, где R0 <С R - Рассмотрим достаточно большой радиус оси валика с тем, чтобы температурное поле ранее наложенных участков шва не влияло на температурные поля последующих участков. Используем второй способ уточнения, который дает, что активную пластическую деформацию сжатия а (Тк — Т0) получают все элементы, оказавшиеся внутри кольца, внутренний и наружный
радиусы Д, и Д2 которого определяют как средние между радиусами окружностей, соприкасающихся с изотермами Тк и Ту предельного состояния нагрева с внутренней и наружной стороны линии перемещения источника. Тогда задача определения сварочных деформаций и напряжений исходного листа сведется к определению деформаций и напряжений составного листа, получающегося путем сшивания кольца II с внутренним и наружным радиусами Ді = Ді II— а (Тк—Го), Д2 = Дг П—а (Гк — — Тп)1 с диском / радиусом ^ис круговым кольцом III, имеющим радиусы R2 и R.
Для диска / и кольца II останутся справедливыми соотношения (8.74) — (8.85). Если предположить, что кольцо III после сшивания останется в упруго-деформированном состоянии, то радиальные смещения и напряжения в его точках определятся соотношениями:
/ЛЗ)
н<3> = cpv + -2~
1 1 Г 1
|
с!3) |
|
(8.91) |
|
о<3) |
|
1-й Е |
|
„(3) Ое |
|
I М3) , 1-й С23) 1-й V 1 + 1 + й |
|
Г<з> I — [1 ^2 |
|
1 + й |
Условиями сшивания в данном случае будут: б1а<1)(Д1) = б2а)2) (Д,); - с<2)(£) = 0;
|
Ое2) ‘ |
Ч1) = ^2,(Ю;
|
(8.92) |
62с<2) (Дг) = 6ю)3) (Д2); ст<3> (Д) = 0;
I (Лі) I + «‘2) №) = R& (ТК - Т0); й<2) (Д2) + 1«<3> (Д2) | = Я г« (Тк - Г0),
где принято Ді = Дь Дг = Д2.
Эти условия, если иметь в виду соотношения (8.74) — (8.85) и (8.91), дадут следующую систему уравнений для определения постоянных интегрирования:
hlEC1 д ( С22 Ргі^і .
! - й 2 V 2С21 / ’
^•22___ Pail р.
І 2С21 - и>
_Pg»E - - 0;
lU 2 С21
Р216 1 ^*2 ^22 |__ 2Р 22^
|
1 + Х2 £х. (1 + ^2)С21’ |
|
с21] _ Й1£ f г<3) _ [6] — ц ' •• ' Cl ' f р С<3> |
|
Г(3) _ 1 — Р С2 Ul 1 + р /г* ’ 3021^1 m_1 Сг2 + 2С21 / С22 , ЗР-Л^І |
|
ббсд—1 V я? 4c|j = Rra (Тк — То); I — 2?., Сг2 , ЗР22^2 |
|
2 і____ ■ * 1+^2 /ф 1 (1+Я2)С21 |
|
б2 |
|
зГ1 (l — Х2 + х|) с|2 3^22^2 |
|
(і+Ч)2Я2Яг (1 hhfch |
|
6Ga" |
|
m— 1 |
|
^22__________ 1___ р22^2 (1 + ^)^ ^ (1+Х2)С2: cf> 1 —р V”1 1 + р |
|
-Cx^ |
|
(8.93) |
|
X |
, 3(l — Х2) Р22^2^22 1 2
+-(1 + ^^с21 J
С(з)
_Сад ^-=:R, a(TK~T0).
Первые шесть уравнений этой системы дадут: п 6lR1EC1
|
Q |
|
21 |
|
(8.94) |
|
«■-«MW 1 _____________________ 261R1EC1 ______________ C21 62(l-p)P22|2 [l-(-^-)2J |
|
в2(1-Р) P2lS2 [J-(-|-)2] |
|
261R1£C1i?^ |
|
22 — |
|
2RXR%CX |
[- |
ЫгГ' |
1 . |
|||
|
(i + h) R2l2 [!-(д 2(1 +и) Ri&A [ |
ти -Ш1 |
f R К R.+1 |
] |
j |
||
|
(1 + *,)(1-ц) І2 [ |
-( |
Ri, 1 |
)’][- |
-( |
Ri > R > |
П |
|
[i + 6 |
W] |
|
|
[■-( |
;t) |
n |
|
X |
|
m-1 |
Остальные два уравнения этой системы примут вид:
(1 + И)
—С,
ЗЄ2(1-Р)
(5+С,
х
62(1-P)as
m— 1
|
Х[14_3(х)4] 2 =«<?*-т*.); (І)[3-(1-2Я,)(І)1-+1] |
|
( 26XRXECX ) |
|||
|
j(l + X2)(I-[x) Vsi |
[.-I |
№ |
П1 |
|
X |
|
X |
|
(1+H)0S |
|
X |
|
(8.95) |
|
-3(1 - h) 2^1 |
m |
m-1 ,-lj 2 g b+! ?. 1 |
||
|
(1 + К) S2 |
[-( |
m |
n |
|
|
X |
Используя тот факт, что искомое значение t находится внутри узкого интервала между R1 и R2, нетрудно найти из этой системы величины Сх и I, а затем по формулам (8.94) — значения остальных постоянных интегрирования, знание которых полностью определяет деформированное и напряженное состояние составного листа. Для определения Сх и £ можно задаться несколькими
значениями £ в интервале между 7?„ Д2 и для каждого из них численным решением уравнений (8.95) найти соответствующие значения С1 и С” по первому и по второму из этих уравнений. Тогда координаты точки пересечения кривых С (£) и СЇ1 (1) дадут искомые значения Сг и
Опытная проверка
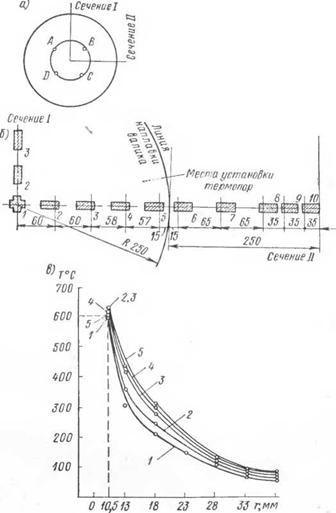
Для опытной проверки полученных выше результатов были использованы листы толщиной б = 10 мм стали типа СХЛ. Из исходных листов, подвергнутых предварительному отжигу в заводских условиях, был вырезан образец 07, имеющий форму кругового диска радиусом R = 50 см. На этом образце наносилась окружность радиусом R0 = 25 см, вдоль которой наплавлялся валик. В данном случае эта окружность разбивалась на четыре части: АВ, ВС, CD и DA (рис. 39, а) и наплавка валика производилась по участкам с двух сторон. Сначала валик наплавлялся от А к В с одной и затем с другой стороны листа. После этого двусторонние валики наплавлялись последовательно от D к С, от В к С и от D к А. Наплавка производилась при постоянном режиме сварки. Измерение температуры зоны валика производилось путем одновременных отсчетов по восьми гальванометрам, которые были подключены к восьми термопарам. Схема установки термопар приведена на рис. 39, б. Первая термопара была установлена на расстоянии 8 мм от оси валика, вторая — на расстоянии 10,5 мм, третья — на расстоянии 13 мм, четвертая — на расстоянии 18 мм и все последующие через каждые 5 мм. На рис. 39, в приведены температурные кривые 1—5, соответствующие отсчетам 7, 8, 9, 10, 11. Оказалось, что температурная кривая 3 отсчета 9 может быть принята за температурную кривую предельного СОСТОЯНИЯ. Используя эту кривую, получим R1 = = 23,3 см, R% = 26,7 см. Далее с известным основанием можем принять, что кольцо II может деформироваться лишь по мере деформации более жесткого металла крупнозернистой зоны, для которой as = 5340 кПсм2. Тогда, принимая Е = 2-Ю6 кГ/см2, т = 13, и = 0,3, Х2 = 2,26 (п. 41), R = 50 см, а = 12,5-Ю"6,
Тк — 7’о = 600° С, решением системы (8.95) получим г] = =
= 0,977, СТ = —70-10“6. При этом формулы (8.94) позволяют определить численные значения остальных постоянных интегрирования:
= — 131 10-6; С£3) = — 244- 10-вД2.
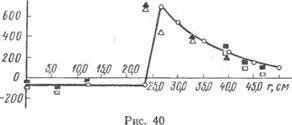
Деформации и напряжения в отдельных зонах определяются формулами (8.74) — (8.85), (8.91). На рис. 40 приведен график полученных таким образом теоретических значений радиальной деформации составного листа (0). Для опытного определения радиальных деформаций этого образца были использованы проволочные датчики сопротивления, которые приклеивались к нему в двух взаимно перпендикулярных направлениях I и II как с одной (1, 2, . . ., 10), так и с другой (Г, 2', . . ., 10’) его стороны в соответствии с рис. 39, б, причем датчики с одинаковыми номе-
|
Рис. 39 |
рами (например, 1 и Ґ и т. д.) располагались как можно точнее друг против друга. Датчики 1, Г, 2, 2', 3, 3', 8, 8', 9, 9', 10, 10' были приклеены до наплавки валика и их показания контролировались до тех пор, пока не становились устойчивыми. После этого по ним снимались начальные замеры и производилась наплавка валика. Последующие замеры по этим датчикам производились после наплавки валика и полного остывания. Сравнение значений радиальной деформации для одного и того же г, полученных по показаниям датчиков, приклеенных с двух сторон листа до наплавки, показало наличие значительного коробления листа после наплавки и остывания. Поэтому для исключения влияния коробления использовались средние значения радиальной деформации по показаниям каждой соответствующей пары датчиков, приклеенных друг против друга, которые обозначены на рис. 40 значками □, ЧЯ соответственно для направлений I и //.
Проведенные замеры не охватывают зону интенсивного нагрева,, Поэтому старые датчики были удалены и в соответствующих точках приклеены новые датчики 5, 5', 6, 6', 7, 7', 8, 8’. После не-
|
ег-1С6
|
обходимой сушки и стабилизации показаний по ним снимались начальные замеры. Последующие замеры по ним снимались после вырезки каждой пары датчиков на строгальном станке. Датчики 8, 8' направления I и датчики 6, 6' направления II, приклеенные после наплавки валика и остывания, дали неправильные показания после вырезки из-за повреждения при вырезке. Полученные значения радиальной деформации в остальных точках этих двух направлений / и II также указывали на наличие коробления листа, В силу этого для исключения влияния коробления были использованы средние значения радиальной деформации по показаниям каждой соответствующей пары датчиков. Эти средние значения деформаций для каждого г, полученные по показаниям датчиков, прикленных после наплавки и остывания, также нанесены на рис. 40 значками Д, а соответственно для направлений I и II. Сравнение всех этих средних опытных значений радиальной деформации (О, is, Д, а.) с ее теоретическими значениями (кривая) указывает на их удовлетворительное соответствие. Вместе с тем необходимо отметить, что в расчетах деформаций не учитывалось влияние неодновременное™ наложения шва, а в опытах сварной шов накладывался неодновременно как по участкам, так и в пределах каждого участка с той и с другой стороны листа, Полученные результаты показывают, что влияние неодновременное™ наложения шва не является существенным.