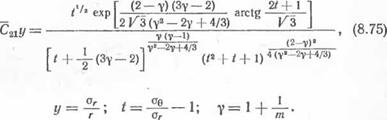СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ В ТОЧКАХ ЛИСТА, ВЫЗЫВАЕМЫЕ ВВАРКОЙ ЗАПЛАТКИ КРУГОВОЙ ФОРМЫ

Рассмотрим деформации и напряжения в точках большого листа с круговым отверстием, возникающие в результате вварки заплатки круговой формы в его плоскости. В этом случае линией перемещения источника будет окружность. Как известно [103], температурное поле источника, перемещающегося по кривой, не изучено. Рассмотрим случай, когда полуширина изотермы Тк достаточно мала но сравнению с радиусом отверстия, и температур­ное поле подвижного источника не получает существенных иска-

жений от влияния температуры ранее наложенных участков (п. 38, 39). При этих условиях, как показали наши опыты (п. 38, 39), полосы цветов побежалости представляют круговые кольца с тем же центром и температурное поле источника, пере­мещающегося по окружности, может быть исследовано методом, разработанным в работе [103]. Обозначим через и радиусы окружностей, соприкасающихся с подвижной изотермой Тк с вну­тренней и наружной сторон линии перемещения источника. В первом приближении можно пре­небречь влиянием температурного состояния всей области, где в предельном состоянии нагрева Т ^ Тк, т. е. принять что во всей этой области Т = Т0. Тогда в соответствии с основ­ной гипотезой каждый элемент, оказавшийся внутри изотермы предельного состояния нагрева в момент достижения его температурой значе­ния Тк, при остывании получит пластическую деформацию сжатия а (Тк—Г0). Если при прохождении электрода по окружности каждый из таких элементов в указанный момент осво­бодить от остального листа, то получим диск радиусом Ru лист с круговым отверстием радиусом R2 и круговое кольцо с внутренним радиусом R = R j [1 — а (Тк — Т0) ] и наруж­ным радиусом R2 -= R 2 [1 —(Тк— Т0) ],

имеющие равномерную температуру Т0.

При этих условиях задача определения приближенных значений деформаций и напря­жений, возникающих в точках листа после вварки заплатки и остывания, сведется к определению дефор­маций и напряжений составного листа, получающегося в ре­зультате сшивания кольца 11 с диском / и с листом 111, имеющим круговое отверстие (рис. 37). Для получения удовлетво­рительных количественных результатов необходимо учесть пласти­ческие деформации нагрева тех областей, где в предельном состоя­нии нагрева Т < Тк. Для учета этих пластических деформаций используем первый способ уточнения (п. 31). В данном случае этот способ дает, что активную пластическую деформацию сжа­тия а (Тк — Т0) получают все элементы, оказавшиеся внутри кольца, внутренний и наружный радиусы и R2 которого оп­ределяются как средние между радиусами окружностей Тк и Ту предельного состояния нагрева с наружной и внутренней сторон линии перемещения источника. Тогда по второму методу (п. 29) задача определения сварочных деформаций и напряжений исход­ного листа сведется к определению деформаций и напряжений составного листа, получающегося путем сшивания кольца с вну­тренним и наружным радиусами R = R^ [1—а (Тк—Т0)1,
#2 = /?2 II —к (Тк— 7"0) 1 с диском радиусом R^ и с листом, имеющим круговое отверстие радиусом R2 (рис. 37). Если исход­ные заплатки и лист из одного и того же металла и имеют одну И ту же толщину б!, то ясно, что диск I и лист III будут состоять из того же исходного металла толщиной 6t. Механические свой­ства металла кольца, а также его толщина, вообще говоря, будут функциями радиуса г. Для простоты используем среднее по ши­рине кольца значение его толщины, которое обозначим через б2. Так как деформации кольца, как целого, будут происходить лишь по мере деформации крупнозернистой зоны, то с известным ос­нованием можно принять, что это кольцо целиком состоит из металла крупнозернистой зоны с пределом текучести os. В зави­симости от пределов текучести исходного металла и металла крупнозернистой зоны, а также от величин 6lt б2, R2— R і, а (Гк—Г0) после сшивания могут оказаться в *упруго-пласти - ческом деформированном состоянии как кольцо и диск, так и не­которая кольцевая область вокруг отверстия листа. Но при при­меняемых на практике режимах сварки разность — R і мала по сравнению с Rt (или R2), в силу чего кольцо будет обладать меньшей геометрической жесткостью, чем диск и лист с отвер­стием. Поэтому естественно предположить, что после сшивания кольцо целиком окажется в упруго-пластическом деформирован­ном состоянии, а диск и лист с отверстием — в чисто упругом.

Ограничимся случаем, когда диск и лист такой толщины, что при нагреве и после полного остывания не имеет места потеря устойчивости плоской формы равновесия. Кроме того, если между диском и листом нет начального зазора, то в соответствии с ос­новной гипотезой и принятым здесь способом уточнения все элементы,"'оказавшиеся внутри кольца R1<;r^R2 в предель­ном состоянии нагрева, должны иметь активную пластическую деформацию сжатия а (Тк — Г0) и в радиальном направлении. Но на практике между свариваемыми элементами допускается начальный зазор до 1,5 мм и при принятых на практике режимах сварки температурное расширение в радиальном направлении не перекрывает этот зазор. Следовательно, в данном случае ак­тивных пластических деформаций сжатия в предельном состоянии нагрева в радиальном направлении не будет. Вместе с тем на­плавленный металл в момент остывания до Тк будет иметь актив­ную деформацию радиальной (поперечной) усадки а (Тк — Т0). Если обозначим через 5 ширину наплавленного металла, то со­ответствующее свободное сокращение поперечного размера на­плавленного металла к моменту полного остывания будет 5а (Тк — — Т0), в силу чего внутренний и наружный радиусы кольца со­ответственно будут:

Ж = Rx [1 - а (Тк - Го)] + - f Sa (Тк - Го);

Ж = R2 [ 1 _ а (Гк — Го)] 5а (Гк - Г0).

Рассмотрим случай, когда S > Ru т. е. не будем учитывать влияние поперечной усадки.

Диск I. Этот диск находится в условиях однородного упругого деформированного состояния и для него получим:

Кольцо //. Примем, что кольцо целиком находится в условиях упруго-пластического деформированного состояния. Для полу­чения однозначного решения задачи сшивания необходимо учесть упрочнение металла кольца, так как схема идеальной текучести не дает возможности удовлетворить условиям сшивания одно­значным образом. Попытка использования известного решения полярно-симметричной задачи пластичности при линейном упроч­нении приводит к тому, что условия сшивания дают систему сложных трансцендентных уравнений, решение которой сопряжено с большими трудностями. Поэтому используем решение полярно - симметричной задачи пластичности при нелинейном упрочнении [116]. Первый интеграл в этом случае дается соотношением (7.51):

Так как внутри кольца R г ^ R2 нормальное напряжение ог меняет знак, обращаясь в нуль при некотором г = £, то следует рассмотреть две области:

R і г ^ I, где or 0;

где о, Ss 0.

1. Область, где аг^0. В этой области при изменении г в пределах от R г до | переменная t изменяется в пределах от неко­торого отрицательного значения до —оо. Как показано в п. 38, в этом случае соотношение (8.75) с достаточной для практики точ­ностью может быть аппроксимировано функцией

(8.76)

где р21 = 0,224. Откуда

ИЛИ

,Д2) ^22 $2Г /О Т7

°г ~ ~г 2С^' (8-77)

Вместе с этим из уравнения равновесия получим

оЬ2) = — фі-г. (8.78)

С21

При условии несжимаемости материала соотношения Генки дадут:

р(2) о ^21 Q2 .

* — z г ; »

6G г

„(2) = _ Ф21 6 6G

Используя формулы (8.77), (8.78) для модуля упрочнения (7.40), получим

С|2 зр2у

/ X/ m—1 ^ ^ ^Cni /

*“=(тг) =-------------- ^— <8-80>

где tn и as— соответственно показатель упрочнения и предел теку­чести металла крупнозернистой зоны кольца. Соотношения (8.79) и (8.80) для радиального смещения в этой области дадут

SHAPE * MERGEFORMAT

ы<2) = 42v _ _ (С22. ^' 2 c2i ) (+

г ь,->1 1 ,2 “ .

6Go--1 v '2 +1ІГІ ' (8'81)

2. Область, где 0. В этой области ог >0, ое > 0,

причем всюду -^->1. Поэтому переменная і при изменении г

в пределах от £ до /?2 будет убывать от -|-оо до некоторой положи­тельной величины, не обращаясь в нуль в рассматриваемом про­межутке. В этом случае соотношение (8.75) можно аппроксими­ровать при помощи функции

г^=тНг - <8-82>

Последняя, как показывает табл. 17, при р22 = 4,6, Я2 = 2,66 удовлетворительно аппроксимирует функцию (8.75). Максималь­ная погрешность имеет место вблизи t = 1. При всех других зна­чениях t в интервале 20 ^ t ^ сю погрешность не превосходит

204

Таким образом, мы нашли выражения составляющих напряжения и деформации для диска и кольца. Те­перь найдем аналогичные выражения для листа с отверстием.

Лист III. Лист с отвер­стием будет находиться в упруго-деформированном состоянии и для него по­лучим:

и<3> =

(8.86)

(1+И) г21

С3Е

(1+р)/-2'

(1 I Я2) С21 Г (і — Я2 + Я2) С;

(1+Я2)2/?^

__m—1

_______________ 3(1-------- Я2) ^22^2^22

^(І+Я^С2! 1 (1 + Я2)2/фС21

~-^ = Ria(TK-T0). Первые пять уравнений этой системы дадут:

У-й* [i-(f)1] ’

_________ 261R1EC1

(l-p)62P2iS2 [l-(x)1 '

26

(I-t0 62P22^[l-(-|L)2] ’

2 (1 + Iі) Г/_____ І Х^аЧ"1

(1-р)(1+Я2П2[і-(^-)2]

где Cx и определяются из последних двух уравнений системы (8.88), которые, имея в виду (8.89), можно привести к виду:

Ся =

[1+3(“г)2Ь

6 G

62os(l — р) [l — ]

m—1

x[l+3(-|-)4] 2 С? = а(Тк-Т0У,

»■ [о-ад (-t )“■'-!]„

+ 3 — 3(1 — hi) {4гУ'++

Lib Lj - с,=«(Г, - r„>.

(і—и) (1 +>*) 6* Li —J

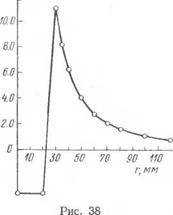
Так как искомое значение | находится внутри достаточно узкого промежутка между Rx и R2, то в каждом конкретном случае при­ближенное решение системы (8.90) может быть найдено без осо­бого труда. Например, при Е = 2-10® кГ/сма, os = 5340 кГІсм2, m = 13, р = 0,3, а = 125-10 7, Тк —Т0 = 600° С, = 1 см, 62 = 1, 2 елі, Я2 = 2,26, R! == 20 он, i?2 = 30 см найдем Сх «=« —3,55-10 4, | = 23 см. Зная Сг и |, по формулам (8.89) можно найти значения остальных постоянных интегрирования. Тогда по соответствующим формулам (8.74) — (8.86) найдутся напря­жения, деформации и радиальное смещение в любой точке со­ставного листа. Для иллюстрации на рис. 38 приведена кривая

полученных таким образом теоретических значений радиальной де­формации ет при принятых выше численных значениях основных параметров. Нетрудно также убедиться, что в данном случае диск и лист с отверстием действительно находятся в упруго - деформированном состоянии:

о'1) (R,) = о(в1) (Ri) —1000 кГ/см2',

с<3) (Rz) = —4а) (R2) = 1680 кГ/см2,

а кольцо — целиком в упруго-пластическом.

е,- W4