СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ В ТОЧКАХ ЛИСТА, ВОЗНИКАЮЩИЕ В РЕЗУЛЬТАТЕ ЗАВАРКИ ЗАКЛЕПОЧНОГО ОТВЕРСТИЯ
Теоретическое решение задачи
В этом случае отверстие относительно малого радиуса заваривается по кругу электродом, диаметр которого сравним с радиусом отверстия. Поэтому здесь температурное поле, вообще говоря, будет аналогичным температурному полю неподвижного источника длительного действия. Если а, — начальный радиус отверстия, а — радиус изотермы Тк предельного состояния нагрева, то ясно, что а > ах. В предельном состоянии нагрева, т. е. в момент окончания заварки, часть листа, содержащаяся внутри изотермы Тк, будет иметь активную пластическую деформацию сжатия, главное значение которой будет равно а (Тк — Т0). Другими словами, если часть листа, содержащуюся внутри изотермы Тк, в момент выравнивания ее температуры до Тк при остывании освободить от ее остальной части, то она к моменту полного остывания получит относительное уменьшение своих размеров в плоскости на величину а (Тк — Т0) = е(/']. При этих условиях задачу определения приближенных значений деформации и напряжений листа после заварки отверстия и остывания, используя второй метод, можно свести к определению деформаций и напряжений составного листа, получающегося в результате сшивания листа с отверстием радиусом а с диском радиусом а' = = а [1 —а (Тк— Т0)1. В результате сшивания в упруго-пластическом деформированном состоянии могут оказаться как диск,
|
так и некоторое кольцо с внешним радиусом b вокруг отверстия листа, а остальная часть листа останется в упругом состоянии. Рассмотрим эти задачи. Используем первый способ уточнения, а именно, примем, что в предельном состоянии нагрева диск радиусом с получил активную пластическую деформацию сжатия ег = а (Тк— Т0), где с— радиус окружности, являющейся средней между изотермами Тк и Ту (п. 31). При этом задача сведется к сшиванию диска радиусом сх = с [1 — а (Тк—Г0)] с листом с круговым отверстием радиусом с. Диск 0 г ^ сх. Обозначим через of* предел текучести материала диска. Диск после сшивания будет находиться в однородном напряженном состоянии „(і) _ „(і) _ п(і) Ог — 00 — us • Считая материал диска несжимаемым из соотношений Генки: ■°е); — — (2о0 — аг) |
|
Єг=^г(2ог- |
|
(8.70) |
|
6 G |
|
получим |
|
(1) |
|
„(і) |
|
о{ 1) |
|
6 G |
|
и, следовательно, |
|
ы<0 |
|
(8.71) |
|
6 G |
|
При этом уравнение совместности деформаций |
|
dee, dr ^ |
|
ев - |
|
(8.72) |
|
0 |
|
даст |
|
фі = const. |
|
Кольцо с с г sS b. Здесь можно использовать полученное в п. 30 решение. В этом случае, как показали опыты, средний предел текучести металла диска о'1' = 3750 кГ/см2, а предел текучести рассматриваемой стали типа CXJ1 сг.‘2) = 3440 кГ/см2. а( 2) Формула (7.35) в этом случае при о0 = of*, k а = с = V з = 2,9 см для радиуса пластической зоны дает b = 4,65 см. Условия сшивания (7.22) в соответствии с (7.23) и (8.71) напишется в виде |
|
3D |
|
(1 + р) bc exp J^~2— (arcsin |
|
4-)] |
|
ф1а<1)с 6 G |
|
2k |
|
— са(Тк — Т0). |
Последнее в точности совпадает с уравнением (7.36), полученным для этой же задачи методом мгновенного охлаждения. Уравнение (8.73) при Е = 2-Ю6 кГ/см2, ц = 0,3, с = 2,9 см, b = = 4,65 см для модуля пластичности дает фх = 3,81.
Для радиальной деформации в отдельных зонах в соответствии с формулами (8.71), (7.37) получим:
^,= (‘ + ^'°-1>, О^с;
|
2 (1 + р) 6 (ст<2))3/2 ехр [— (гр — л + arc sin |
|
КЗ |
|
(2) _ |
|
е |
|
3 сЕ |
|
е |
|
Ь^-Г^ОО. |
|
|
|
КЗ Е |
|
Рис. 35 |
(3) _ 1 + р „(2)
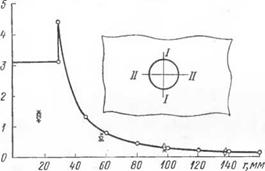
На рис. 35 приведена кривая теоретических значений ег (0), подсчитанных по этим формулам.
Опытная проверка
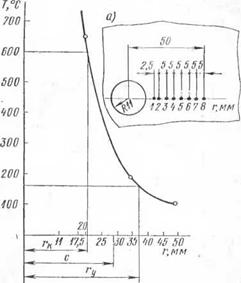
Для проверки полученных выше результатов был взят лист отожженной стали типа' CXJI, размера 50Х50ХІ см, имеющий центральное отверстие диаметром 22 мм. Отверстие заваривалось по кругу при помощи электрода. В процессе заварки производились замеры температуры при помощи восьми термопар путем одновременных отсчетов. Схема установки термопар приведена на рис. 36, а. На рис. 36, б приведена температурная кривая предельного состояния нагрева. При расчетах принято Тк =
|
|
|
б) |
|
115. 41 |
|
41 |
|
41 |
|
О |
|
Гг7^Сечеиие11 |
|
’ZZZ&X |
|
-га- 2 П 3 Рис. 36 |
|
= 600° С, То — 0 и, как нетрудно подсчитать, Ту = 160° С. клеивались после заварки После сушки и контроля Последующие замеры сни- Данные замеров приве- . /—I сверху, V — для ' -1 то же для сечения / /—II соответственно формаций и применяемый теоретическое значение упругой Тчасти радиальной деформации |
|
Остаточные деформации по сечению 1—I в результате заварки заклепочного отверстия
|
|
Остаточные деформации по сечению II—II в результате заварки заклепочного отверстия
|
Необходимо отметить, что примененный здесь способ уточнения теоретического решения обеспечивает хорошее совпадение теоретических и экспериментальных данных несмотря на то, что в данной задаче имеем источник длительного действия, создающий широкую зону между изотермами Тк и Ту. Этот способ уточнения дает не менее хорошие результаты и при подвижном источнике. Необходимо отметить, что экспериментальное исследование температурных полей и остаточных деформаций при дуговой заварке отверстия в плоском стальном листе дано и в работе [6], где указывается, что тензометрические измерения подтвердили возможность расчета остаточных напряжений по ранее предложенному методу [7]. Вместе с тем в работе [17] отмечается, что результаты решения этой задачи по методу [7] существенно отличаются от опытных данных.