СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ КРУГОВОГО ДИСКА, ВЫЗВАННЫЕ НАПЛАВКОЙ ВАЛИКА НА ЕГО КРОМКУ
Теоретическое решение задачи
Рассмотрим сначала теоретическое решение этой задачи на базе основной гипотезы. Возьмем сплошной круговой диск постоянной толщины и достаточно большого радиуса R с тем, чтобы в процессе наплавки валика его начальную равномерную температуру Т0 можно было считать неизменной. При этих условиях каждый элемент, содержащийся внутри изотермы Тк, к моменту достижения температуры Тк внутри него при остывании в направлении перемещения источника получит пластическую деформацию сжатия, приближенное значение которой определится величиной а (Тк — Т„).
Если этот элемент в указанный момент освободить от остального диска, то к моменту остывания до начальной температуры Г0 он получит относительное уменьшение своих начальных размеров в указанном направлении "на'величину а (Тк— Г0). Освобождая аналогичным образом последовательно все элементы в моменты достижения температуры Тк при их остывании в процессе прохождения электрода по всей кромке диска, вместо начального диска пулучим сплошной диск радиусом Ri <С R, где R г — радиус диска, контур которого соприкасается с подвижной изотермой Тк предельного состояния нагрева, и круговое кольцо с наружным радиусом R' = R (1 — е[р)) +6' и внутренним радиусом R2 = = R]_( 1—ег), где б' — толщина наплавленного металла. При этих условиях, если использовать второй метод, задача определения приближенных значений сварочных деформаций и напряжений начального сплошного диска сведется к нахождению деформаций и напряжений составного диска, получающегося в результате сшивания диска с кольцом.
Другими словами, задача определения приближенных значений сварочных деформаций и напряжений исходного диска
сведется к определению 00 из условия:
I up т I + «г2) (Rz) = RAp)- (8.58)
Рассмотрим эту задачу.
Сплошной диск. Диск будет находиться в условиях однородного напряженного состояния
О г — 00 = 0О
и в силу его большой геометрической жесткости по сравнению с геометрической жесткостью кольца, он, как увидим ниже,
будет находиться в упругом состоянии. При этом будем иметь
= —U-^-0or. (8.59)
Кольцо. Это кольцо в силу его малой геометрической жесткости будет находиться в условиях полярно-симметричного упруго-пластического деформированного состояния. Решение этой задачи дается формулой (7.51). Металл этого кольца по его радиусу не будет однородным. С известным основанием можно считать, что при действии 0„ оно будет деформироваться лишь по мере деформации жесткого металла крупнозернистой зоны. Поэтому примем, что это кольцо целиком состоит из металла крупнозернистой зоны. Для металла этой зоны имеем os = 5340 кГІсм2,, т = 13 (п. 31). С целью некоторого упрощения расчетов примем т= 12,82.Тогда соотношение(7.51) в этом случае перепишется в виде:
|
СіУ = „ , , , ,10,624У • (8-6°) |
— Y ~t exp (о,969 arctg * j
(t + 0,619)‘/‘ (<2 + t + l)0-'
Так как 0e > 0, a, <i 0 во всех точках этого кольца за исключением точки г = R', где 0Г = 0, то отсюда следует, что в рассматриваемой области переменная
t=*L-
ог
везде отрицательная и, как увидим ниже, удовлетворяет условию
— —25.
Для каждого значения t, заключенного в этом промежутке, функция
(t 0,619)v* = tu = |^i |‘Л (cos п j 1 я + і sin п~^-- ,
п = 0, 1, 2, 3
будет иметь два комплексных значения (п = 0; п = 2), одно вещественное отрицательное значение (п = 3) и одно мнимое значение (п = 1). Так как отношение -^-вещественно, то, как это
сдедует из (8.60), комплексные значения t/l должны быть отброшены. Остальные два значения /'/* будут отличаться друг от
друга лишь постоянным множителем, в силу чего вместо (8.60)
примем
|
Cl у — |
|
(8.61) |
V 11 exp ^0,969 arctg j
|6 |V.(^ + /+ 1)0.624 *
Эта функция может быть аппроксимирована соотношением
|
Р |
|
(8.62) |
|
t+ 1 |
|
Сі У — |
|
В табл. 14 приведены значения функций Сху для некоторых значений t, найденные по формулам (8.61) и (8.62) при р = 0,224. Нетрудно проверить, что аппроксимирующая функция (8.62) |
|
2 R |
в весьма узкой зоне вблизи t = —100 дает максимальную погрешность 14% и вне интервала —150 sS < t —50 — менее 5 %. Подставив теперь значение t из (8.62) в соотношение (7.53) и проинтегрировав, получим
7*
Г =
_Р_
V Cj
где Сх и С2 — постоянные интегрирования. Отсюда получим
f 21/:
Р'
2С<
|
Таблица 14 Значения функций Сху при изменении аргумента в интервале —400 ^ t ^ — 25
|
Определив С] и С2 из условий:
<*г (Яа) = —«V.
О, (R') = о,
|
(8.63) |
будем иметь:
2ст„
Од = •
Ш’- *
Найдем теперь uf]. Для этого используем соотношение
efi2> = (2о0 — аг).
|
°0 |
г1! |
5 1 |
1 f |
|
«г1 |
to 1 1 I- |
j m—1 [ |
|
г[* + (^)Т |
|
т-1 |
|
О? |
( R. ) |
m 1 r |
|
|
6Ga'” -1 [ |
m 1 |
|
~ «Л3 + ( ' ) ] ’ |
|
Имея в виду, что в этом случае: 2ае — а, = |
т-1
е(2>= “г Г* уА^7ЛХ*^(КЛ*Гг~
SHAPE * MERGEFORMAT

получим
... . ( а0 rn-l т—1
(8.65)
Подставив последнее вместе с (8.59) и (8.58) и полагая Rlt
будем иметь
|
т-1
|
£е<Р)
Ч" = (Т=^.<8.66)
а0
где Г) =—!5-
Последнее уравнение определяет (Т0.
Опытная проверка
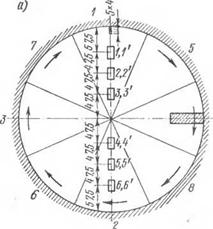
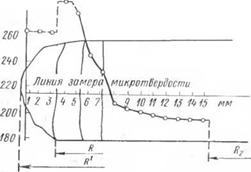
На кромку диска стали типа CXJI был наплавлен валик, показанный на рис. 32, а, где X — термопары; □ — датчики (на обратной стороне датчики наклеены симметрично); заштрихованный прямоугольник — образец для микрошлифа; —> — направление наплавки. Температура в зоне валика контролировалась четырьмя термопарами. Замеры показали, что изотерма Тк = = 600° С отстоит от кромки диска на расстоянии 6 мм. На рис. 32, б приведена схема зон термического влияния и кривая микротвердости, характеризующая неоднородность механических свойств металла зоны валика. Дадим здесь уточненное ре
шение с учетом пластических деформаций зоны, где температура нагрева в предельном состоянии была меньше Тк. Используя второй способ (п. 31), можем принять, что зона, где в результате нагрева и остывания произошли изменения механических свойств основного металла, получила пластическую деформацию сжатия а (Тк— Т0) — е[р).
|
|
Тогда в соответствии со схемой нарис. 32, б для внутреннего и наружного радиусов кольца 'получим R2^ R і =
= 18,8 см, R' = 20,25 см.
При этих условиях, подставив в уравнение (8.66)
Е = 2-10® кГ/см2, os =
= 5340 кГ/см2 (п. 31),
р, = 0,3, m = 12,82, [.sip) =
= 125-10“7-600° С, в результате решения получим Г] =
—0,0832, т. е. а0=444кГ/см2.
|
В) НцпГ/мм2 |
|
|
Из этого следует, что внутренний диск, как это было принято выше, будет находиться в упругом состоянии. Зная 0О, по формулам (8.59),
(8.64) и (8.63) можно определить деформации и напряжения внутреннего диска и кольца.
На рис. 32, в приведен график^изменения теоретических значений ра - диальной’деформации ег.
|
(U
|
Там же значками О обозначены 'значения полученные путем замеров соответственно с одной и с другой стороны диска, причем датчики 4, 5, 5' не дали показаний. Сравнение полученных теоретических и экспериментальных
значений ет показывает их удовлетворительное соответствие — среднее экспериментальное значение ег превосходит полученное теоретическое значение в пределах внутреннего диска не более чем на 18%.