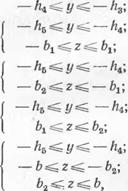СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ БАЛКИ ТАВРОВОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Упругое состояние тавра
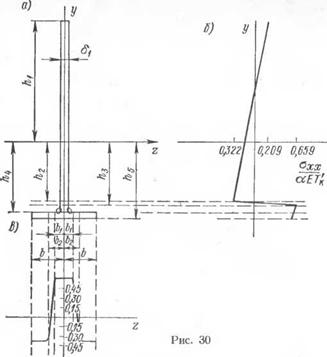
Основные обозначения указаны на рис. 30, а, где /г4 — h3 —• ширина изотермы Тк и 1г3 — /г2 — расстояние от изотермы Тк до границы пластических деформаций в предельном состоянии нагрева по перпендикуляру к огибающей изотермы Тк в точке их касания для стенки; 2Ьг— ширина изотермы Тк и 62— Ьг — расстояние от изотермы Тк до границы пластических деформаций нагрева для полки но одну сторону от плоскости продольной симметрии балки. Среднюю толщину стенки в зоне шва, где —/г4 ^ у ^ —ha обозначим через бь Примем также, что при прохождении электрода стенка и полка нагреваются равномерно
|
|
по толщине. В соответствии с первым методом (п. 29) и первым способом уточнения (п. 31) распределение температуры охлаждения определится соотношениями:
Т = Г(1) = 0;
|
у» 2) |
— Л2 «с г/ < /г,; — ha^y^ — h2
hз
|
|
|
(8.29) |
Т — 7,(8) = — Т'к; Т = Г(4) = — Тк т'
Г=т<и=--брлг(г+^
У __ у(7) __ у(8) _ Q.
где hi + /і8 = /г.
178
Напряжение ахх определится по формуле (8.22), где постоянные Сі и С2 найдутся из условий равновесия внутренних сил в рассматриваемом поперечном сечении тавра. Для этих постоянных получим:
а ЕТ'
С{ — 2qjK [бі(Аз — Аг) {h-2 -)- 2Лз) ф - 36і(/і4 Л*) ф-
Ф - 3 (Ai ф - А2) (^s — А4)];
(8.30)
а ЕТ„
Сг — щг - [бі (Аз — Аг) ф - 26i (А4 A3) ф-
ф - 2(Аіф-.&г) (Ав —А4)].
Деформации ехх, ет определятся по формулам (8.8), а смещения находятся путем интегрирования уравнений Коши:
6Cjxy. 2С%х
и =
SHAPE * MERGEFORMAT

|
(8.31) |
|
3C, jc2 |
v = — - g - [(ЗСхуф-2С2) у] ф-а (1 ф - р.) | Tdy -
где функция Т определена соотношениями (8.29), а постоянные Сі и С2 определяются формулами (8.30).
Для иллюстрации на рис. 30, б, в приведены графики изменения ахх по высоте стенки и ширине полки тавра, где для расчетов принято 81 = 28і = 16 мм, А — 300 мм, А5— Л4 = 6г, А = 50 мм, Aj = 16 мм.
Упруго-пластическое состояние тавра
Обозначим через (—і]), £ и (—£) границы зон пластических деформаций, где —/г3 < —т] —rj2, Аг £ =sS А2, —А2 — £ «£ —Ь1ш Температура охлаждения для упругих и упруго-пластических зон определится соотношениями: упругие зоны:
|
у(2) ___ J*(5) =_____ |
|
Л з — h2 ТІ |
|
62 — fci г' |
|
(8.32) |
|
Г(6) _ |
|
(А2 + ^); (А* + г); (г— AJ; |
|
62 — Г(7) - 0; |
|
7(1) = 0; ті |
|
— hz^y^hi, — ті —Л2; — Л5<г/< —л4; — A2^z< — £; — А5 < у ^ — Л4; £<2=^ А2; — A5sS#< —Л4; — А==^гс— А2; —А6«=с */«£ —А4; |
Напряжения и деформации в упругих и упруго-пластических зонах соответственно определятся соотношениями (8.25), (8.26). Для нахождения постоянных интегрирования Clt С2 и величин г и £ можно использовать условия:
|
j axxdF = 0; |
f axxydF = 0;
|
(8.34) |
|
Jy) ^ХХ Лу) |
(— n) = e« (— ч)г
„(р).
*&'(-£) = «£'(-£)■
|
аЕЬлТг. ,9 |
Эти условия дадут систему:
—6CiS<p)+2C2.F(j/) + o'sF(p) +
|
аЕб1Тк |
|
(8.35) |
|
X |
|
6 (А. —А,) 4 *11-1/ 4(^-6,) X (Л| —Д1)(62 —1)2 = 0; — 6CtT) + 2С2 = (1 + р) Os + аЕТ (—rj); -6Cift5 + 2С2 = 4- (1 + ц) 4 + а£Г (- Q, |
|
Ь2 — —6Сі (л - 4Р)) - 2C2sip) + o'ssip) - аЕТІ |
|
-(Л| —ЗАаГ]2 + 2Т]3) |
|
(62-£)2 = 0; |
где J{zp), SzP) — соответственно момент инерции и статический момент площади f (р> пластической зоны; = F — /г(р);
П-Ч) =
ті
|
Т( £) = ■ |
■(Аа-£).
|
кУ |
|
I / Л5 — т) |
|
(8.36) |
|
2Со |
|
Ь2 — Ь |
|
Последние два уравнения этой системы дадут: а£Г'„ / й,_ч |
|
Q-Zt „ / її eC‘ = T^kU а^гі, ь2_ц ь2_£ |
|
^) + _3_(l+ll)crs + |
|
+ А.-Т, —ті). |
Подставив последнее в первые два уравнения системы (8.35), получим следующую систему для определения величин Г] и £:
аЕТ
+ [(*«—Л'6- + 2fe-4)p“I +
|
■(*■ —£)а = 0; |
аЕб2Тк, и n2
bo — ьл
(8.37)
(JV=JL + AqL) (j __ У(Р) _ S(P)) +
л6 — ч л3 — а2 1 б2 — *1 /
н/;Т„
X
3 52 6 (А,-А,)
X [б^Аа - ті) S<p) + бі (Л| - ЗА2т!2 + 2tj8)] -
а£Т
^г(Л5-А!)(62-£)2 = 0,
4 (fc2 — Ьф
ЛР) — (А3 ’і) (Я т h3t + ц) Ч—g - (hi — h,) (h A4A3 - j - A3) +
+ -3- ? (h5 h^ (hi - f - A5A4 - j - A4);
sip) = 4 № —h)+~ ei (h - hi) +1 (hi - /4);
F(p) = 6j (hs — rj) + 6І (hi — h3) - f 2£ (As — hi).
В каждом конкретном случае при заданных размерах тавра и режиме сварки, характеризуемом величинами (А3 — А2), (А4 — А3), bі, (Ь2— 6 J, из последней системы могут быть найдены т) и £, знание которых определяет деформации и напряжения в точках тавра. Смещения его точек могут быть найдены путем интегрирования уравнений Коши. В упругих зонах последние определяются соотношениями (8.31), где постоянные Сі и С2 могут быть выражены формулами (8.36). Общее изменение формы тавра определяется смещениями упругой зоны стенки.
В п. 32—34 применена приближенная теория сварочных деформаций и напряжений к задачам, где имеет силу гипотеза плоских сечений. Аналогично могут быть рассмотрены другие случаи полос или балок постоянного или переменного поперечного сечення. Для решения этих задач используется первый метод, позволяющий свести задачу определения сварочных деформаций и напряжений к температурной задаче деформируемой среды, где распределение температуры мгновенного охлаждения определяется законом распределения пластических деформаций предельного состояния нагрева.
Применение этого метода расширяет класс решаемых задач, делая возможным использование уже известных решений температурных задач деформируемого тела [8, 15, 26, 59, 67, 68, 80, 91, 92).