СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

ВОЗМОЖНЫЕ ПУТИ УТОЧНЕНИЯ ТЕОРЕТИЧЕСКОГО РЕШЕНИЯ, ПОЛУЧАЮЩЕГОСЯ НА БАЗЕ ОСНОВНОЙ ГИПОТЕЗЫ

Дальнейшее уточнение теоретического решения, на наш взгляд, должно идти в двух направлениях. Во-первых, некоторое превы­шение опытных данных над теоретическими вблизи внутренней границы наружной упругой области может быть объяснено тем, что теоретическое решение для пластической области получено на основе условия пластичности Губера—Мизеса, т. е. без учета упрочнения основного металла зоны термического влияния. Иссле­дование микроструктуры материала зоны точечного нагрева по диаметральному сечению, перпендикулярному к плоскости листа показывает, что материал внутри круга г = а, где температура нагрева была больше или равна Тк, имеет однородную крупно­зернистую структуру, одинаковую со структурой крупнозерни­стой зоны термического влияния вблизи сварного шва (п. 24). Круг г = а крупнозернистой зоны охватывается кольцом с на­ружным радиусом d, содержащим материал мелкозернистой зоны, причем здесь структура зерен совпадает со структурой мелкозер­нистой зоны, существующей вблизи сварного шва. Снаружи этого кольца материал везде имеет исходную структуру. Таким образом, микроанализ полностью подтверждает физическую идентичность явлений, происходящих при сосредоточенном нагреве листа и при сварке встык двух плоских листов или при наплавке валика на кромку плоского листа. Физическая идентичность указанных явле­ний полностью подтверждается также исследованием механиче­ских характеристик металла в отдельных зонах термического влия­ния вблизи сварного шва и в зоне сосредоточенного нагрева пло­ского листа.

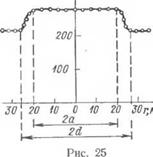
Для иллюстрации на рис. 25 приведена кривая изменения микротвердости в зоне сосредоточенного нагрева плоского листа. Замеры микротвердости производились по диаметральному сече-
нию, перпендикулярному к плоскости листа. Как показывает эта кривая, микротвердость в крупнозернистой зоне на 25% выше микротвердости исходного металла, т. е. примерно настолько же, насколько микротвердость металла крупнозернистой зоны вблизи сварного шва выше микротвердости исходного металла.

Другими словами, в зоне сосредоточенного нагрева после по­следующего остывания существует такое же упрочнение металла, сопровождающееся значительной потерей его пластичности, какое

существует в зоне термического влияния вблизи сварного шва. Выше приведенное решение рас­сматриваемой задачи учитывает повышение предела текучести ме­талла диска г а, но не учитывает его упрочнения в кольце а ^ г С d. Это упрочнение в какой-то мере должно сказаться на увеличении деформаций в зоне внутренней гра­ницы наружной упругой области.

Второй причиной указанного рас­хождения между опытными и теоре­тическими значениями радиальных деформаций должны являться неучтенные основной гипотезой пластические деформации трех частей листа, которые находятся вне изотермы Т — Тк. Рассмотрим теперь эти возможные виды уточнения теоретического решения задачи.

Учет упрочнения основного металла в кольце a

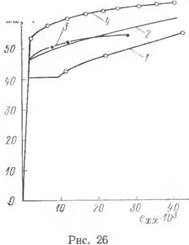
Для выяснения влияния упрочнения основного металла этого кольца необходимо решить полярно-симметричную задачу пло­ского напряженного состояния при нелинейном упрочнении. Как показывает рис. 25, в этом кольце механические свойства металла непостоянны, изменяются вместе с изменением г от их значений для крупнозернистой ЗОНЫ (Г d) до их значений для основного металла в исходном состоянии (г 5» й). На рис. 26 приведены истин­ные диаграммы растяжения основного металла в исходном состоя­нии (кривая 1) и металла крупнозернистой зоны (кривая Д. Каждая из этих диаграмм, если исключить из рассмотрения переходную часть от предела пропорциональности до предела текучести путем повышения предела пропорциональности до условного предела текучести, как показано в работе [ 116 J, с достаточной для прак­тики точностью, может быть представлена формулой

SXX=Y Etf-'et* (7.38)

где Е, as, m — соответственно модуль упругости, условный пре­дел текучести и показатель упрочнения металла данной зоны; елх — полное относительное удлинение.

В рассматриваемой задаче [116] для металла крупнозернистой зоны можно принять Е ^ 2-10® кГ/см2, as = 5340 кГІсм2, т — 13, а для исходного металла Е = 2-Ю6 кГ/см2, cts<=»4050 кГ/см2, т = 215 в пределах площадки текучести. В кольце а ^ г sg d ве­личины crs и т будут изменяться вместе с изменением радиуса, а величина Е при этом будет претерпевать незначительные изменения, так что можно принять Е = const = 2-10е кГІсм2 всюду в кольце a^r^d. Таким образом, в общей постановке рас­сматриваемая задача должна быть решена с учетом переменности $. характеристик о, и т в этом кольце. Так как в данном случае интересен вопрос влияния упроч­нения металла в кольце а ^ г d на ход кривой еТ для всех г >> d, то ограничимся рассмотрением этой задачи для случая, когда характеристики os и гп в пределах указанного кольца остаются постоянными и определяются по средней диаграмме (кривая 2) между истинными диаграммами исходного металла (кривая 1) и металла крупнозернистой зоны (кривая 4). Кривая 3 означает среднюю диаграмму, выражен­ную формулой (7.38) при as =

= 4700 кГ/см2, m = 16. Непосредственно видно, что формула

(7.38) в пределах 2—2,5% полной относительной деформации с достаточной точностью представляет среднюю диаграмму. В этих пределах изменения деформации максимальное откло­нение ординаты кривой 3 от соответствующей ординаты кри­вой 2 не превосходит 2,5%. Поэтому примем, что зависимость между деформациями и напряжениями за пределом текучести для металла кольца а г d дается формулой (7.38) при as = = 4700 кГ/см2, m = 16. Из-за малости рассматриваемых дефор­маций истинное напряжение Sxx практически не будет отличаться от соответствующего условного напряжения, и поэтому фор­мулу (7.38) в последующем будем использовать для условных напряжений. При этих условиях зависимость между интенсив­ностью напряжений ot и интенсивностью деформаций <?,• сложного напряженного состояния с точностью будет совпадать [116] с диаграммой простого растяжения (7.38), построенной в ко­ординатах с,- и ef, т. е. о{ и е£ в этом случае связаны соотно­шением

о і = УЕоХ-%-

10 Г. Б. Талыпов

Аналогичная зависимость между интенсивностью касательных на­пряжений rf и интенсивностью деформаций сдвига будет опре­делена формулой

Т,- = У СтГ V (7-39)

и модуль упрочнения ф может быть представлен соотношением

<7-40>

где т8 —- предел текучести на сдвиг; т — показатель упрочнения, определяемый по диаграмме истинных напряжений растяжения, а ті через главные напряжения о1( а2, а3 определяется формулой

= - ттг-VVi — o2f + (с2 — а3)2 (а3 — щ)2.

1 6

В случае рассматриваемой полярно-симметричной задачи:

°Х = р2 = °3 = О,

в силу чего интенсивность касательных напряжений представится т» — Уо2г — огов + Се. (7.41)

Используя гипотезу о коаксиальности главных касательных напря­жений и главных сдвигов, получим:

Ті Гг т3 G_ ш

Yi ~ Уг ~ Уз ~ Ф ’

°6 = ~рг = аг~ав = 2G

ев~е2 eg-ef ег-ев ф ’

Эти соотношения, если пренебречь сжимаемостью материала, дадут:

er = "gQ - (2®г ог0).

ее^-^№в — °г)

ЄЄ-Єг = -^(°0 — 0>).

Для модуля упрочнения ф в соответствии с (7.40) и (7.41) имеем

При этом еп ев, а также разность последних представятся соот­ношениями вида:

т—1 )

е, = Я {2аг — ае) (а? — а, ае + а%) 2 ;

т—1

е0 = Я (2ае — сгг) (о? — оуа© + ре) 2 5

т-1

2 _ . 2 2

В0 — Вг = ЗЯ (ае — оЛ) (ог — агае -ф ае) 1

Я = -

т+1

2 _ т—V

Из уравнения равновесия

dcr і а г ОД q

dr ' г

имеем

°в=£("*г)-

В силу этого выражения ев и ев — ег перепишутся в виде:

m—1

ее=х(2г4?+с0Н+га^+гЧ^)1 2 ;

т—1

о, dar Г 2 , . 2 ( dar N2") 2

^_C.|ar + Wr_ + r.

Введем обозначение

ф=і+4г=у - <7-50>

Тогда последнее уравнение представится

1 dt

[*»----- 1- (2 — y) t (Зу-2)]

У t [<3 + _3_y/e+.|_y/+_^ (Зу-2)]

откуда

<Vlexp Г (2-у) (ЗУ-2) arctg? i±l

TOC o "1-5" h z j^2 фз ^у2 — 2у + —-) *3

СУ =

У (V—1) (2-УV

У2-2у+ - І 4 | V2 -2V 1--|Л

[<+-L(3y-2)] (** + <+О

где С] — постоянная интегрирования.

Таким образом, задача решается в замкнутом виде для любого показателя упрочнения т [116].

Попутно отметим, что формула (7.51) содержит все решения полярно-симметричной задачи плоского напряженного состояния при нелинейном упрочнении за исключением той, для которой

= 1. Функцию Сгу, определяемую соотношением (7.51), с до-

ог

статочной для практики точностью можно аппроксимировать фор­мулой

Сху^Ае^, (7.52)

которая позволит найти t как функцию у

t = ф (у).

Тогда, имея в виду, что

dy

6 (j у

t_ j л*

■ У

где х = In г, получим

у' = У [ф (у) — 1 ],

т. е.

In г = f - г-?у,, + с2. (7.53)

J у№(у) — В v

Формула (7.52) дает

где х =-р - Это выражение позволяет определить функцию у и, следовательно, радиальное напряжение:

сцг=мч>[р(і + £)]; [•>(>+€)]'

ar = - g - exp

При этом уравнение равновесия даст

°е='5-(2+С)ехрК1+€)]'

Далее, имея в виду, что

2о'-°»=ехр К1+€)];

2ае_с,=-і(з+-£)еХр[(>(і+£)],

из условия коаксиальности главных деформаций и приведенных напряжений

dur иг

dr г

Используем теперь полученные результаты для нашей задачи. При действии равномерного радиального напряжения сг0 в точ­ках контура отверстия вокруг этого отверстия возникнет пласти­ческая зона. Пусть, как и в предыдущем, Ь означает наружный радиус пластической зоны. Как показывает решение этой задачи на основе условия текучести Губера—Мизеса (п. 30), радиус пла­стической зоны Ь больше наружного радиуса кольца а ^ г ^ d.

Поэтому в пластическом состоянии будет также находиться неко­торое кольцо исходного металла шириной b — d. При os = — 5340 кГ/смг внутренний диск г ^ а будет находиться в упругом состоянии. Все величины, относящиеся к этому диску, в дальней­шем будем отмечать цифрой 0 в скобках (например, а,0)). Кольца с г ^ d и d sc; г ^ b будут находиться в упруго-пластическом состоянии и все величины, относящиеся к ним, будем соответ­ственно отмечать цифрами 1 и 2 в скобках (например, о*1', С[Х), СІ1), Сз1 а®, £<2)> Сз2) и т. д.). Внешняя часть листа г b будет находиться в упругом состоянии и все величины, относя­щиеся к ней, будем отмечать цифрой 3 в скобках (например, С[3) и т. д.). Причем легко установить, что радиальное смещение и со­ставляющие напряжения в этой упругой зоне определяются фор­мулами:

С<3>

н<3> = ■

о®’ =

(1+й)'2’

С[3)Е

„(3) __________

00 (1 + |л) г* ■

В выражениях радиальных смещений и составляющих напряже­ний двух упруго-пластических зон и одной наружной упругой зоны будут содержаться семь произвольных постоянных. Для их определения можно использовать следующие условия:

0<Х) (а) = а0;

Orl) (d) = о'2) (d);

o41>(d) = o42,(d); uil) (d) = и?' (d); oi2) (b) = a(r3) (b); e?b) = oP (b)-, u?b) = u?b).

В развернутом виде эти условия в соответствии с формулами (7.54)—(7.57) запишутся:

Решение этой системы будет:

СГ’^ехр [_3Pl(4)-(^)-];

й“ = - т (тГ*”"

с(4— (Н-Юво^1 |о ^ ь yt. jV. tfi-ft.) х х«р{*(4)'[(-5-)--1]+1*,[(4Г-1]};

сР = І^-рН.(ІГ[(-УГ+Ь-і]}; сі» = - ф 6“’;

ср = _('+^>-,-еХр {зр, (4)- [(«.)«■ _ і] + с|3) = Й,/2С^

При этом для компонентов напряжения и радиальной деформации в отдельных зонах будем иметь:

о™ = «ь - Г1“Р {*' (4Г [(4 Г - ( тТ ]};

^-<*-г[*-®(тГ(тГ]х

х«р И4П(4Г-(4Г]Ь

(1) _ (1-І - у)°вь* ^_ь_ул v

х М-э-П-гУТ’'х

хеХР{зр1(4)“‘ [(-!)У"- '] + + з Р. К4Г-1]};

Г»-(4П К4Г-(4ГУ

х ехр (зр, (4)"' [( l] -!

+ 3P,[(4f-.]);

d^r — b:

0р.=в>4ехр{зр1(4)“-[(4)“--1] +

+ *[(4Г-(т)-]}:

„«. = 0.4 [2-3(4)“'] exp {з

х[(4Г-']+зfc[(4)--(4)-]}=

^=<Ш0».(А)(4)(^Х

Таким образом, найдены компоненты напряжений и радиаль­ных деформаций в отдельных зонах для любых значений пара­метров Pj и Р2, зависящих от упрочнения материала. Найдем теперь значения этих параметров в нашем случае для зон а ^ г d и d ^ г ^ b. Для этого сначала необходимо установить пределы изменения переменной t

в этих упруго-пластических зонах. В рассматриваемой задаче (п. 30) or i>0 во всей упруго-пластической и внешней упругой области, а сте, начиная от некоторого г >• а, сначала возрастает, а потом убывает по абсолютному значению, оставаясь отрица­тельным. Из этого следует, что в данном случае могут быть ин­тересны лишь отрицательные значения переменной t. Нетрудно также установить пределы изменения этой переменной. Действи­тельно, при d ^ г s=s Ь по формулам (7.59) имеем

и, следовательно

Откуда при

г = b; t — —2.

С другой стороны, при г = а составляющая о0, как увидим ниже, будет положительна и мала по величине по сравнению с аг = сг0, в силу чего соответствующее значение t будет находиться вблизи —0,9, т. е. можно принять, что в рассматриваемой нами задаче пере­менная t будет изменяться в интервале

и, следовательно, при интересующих нас значениях т = 16 и т = 215 знаменатель соотношения (7.51) не будет обращаться в нуль. Отметим, однако, что правая часть соотношения (7.51) представляет многозначную функцию, обусловленную наличием

, 2t f 1

arctgTT

И

V (v-Ч 1 У*-2у+‘/>

[«+4<э»-2>]' [<+4-(9»-Ч]<°;

—5^5— дробное число.

2 — 2у + о/з ^

Как это общепринято, используем лишь главное значение

arctg Что же касается второй из этих функций, то при

У 3 т = 16 имеем

Vi (Vi—і)

г 1 / v?-2vi+*/.

[* +-2"(3Yi— 2)J

^ (/ + 0,594)°'197 ^ (/ + 0,594)v‘ =

Последнее выражение при заданном і имеет четыре комплексных

значения корня и одно вещественное отрицательное, равное —| ^|. Комплексные значения должны быть отброшены, так как функ­ция у в выражении (7.51) имеет лишь вещественные значения. Таким образом, для зоны, где т1 = 16,

—і У t I exp (о,953 arctg ~L 'j

ГС, у = (7.61)

/t + 0.594 |02 + * + l)0'652

В табл. 10 приведены значения функции — » определенные по

формуле (7.61) в интервале —1,7 ^ t ^ —0,9. Там же даны зна­чения этой функции, найденные по формуле (7.52) при = = —2,43/, р = 1,21.

Непосредственно видно, что максимальная погрешность, полу­чающаяся при применении аппроксимирующей формулы (7.52), не превосходит 4%.

В зоне d^r^b, где ms — 215, функция

У. (Va—1)

1

715

[i +-y (ЗУ*- 2)] "2 2V2+V* ~(* + 0,508)715 = іГ

Значения функций —

С-іУ

для каждого отрицательного значения t будет иметь лишь одно

вещественное отрицательное значение — Vt\- Аналогично пре­дыдущему для этой зоны получим

- iVt exp (о, 875 arctg --U)

Сіу = 71-_ = v =-------------------------- Ш-. (7.62)

11 + 0.508 I (I2 + / + l)0'743

В табл. 11 даны значения функции—определенные по

формуле (7.62), а также ее значения по формуле (7.52) при А2 = = 2,15t, Р2 = 1,10 в интервале —2 і —1,4.

В данном случае погрешность, даваемая формулой (7.52), из­меняется в пределах от —4,5 при t = —2 до 3,8% при t = —1,7.

Наибольшая погрешность в + 9% имеет место при t = —1,4.

Таким образом, имеем следующие значения параметров рх и р2 для упруго-пластических зон:

а ^ г ^ d; Pi = 1,21; v. x = 0,826;

d^r с 6; p2 = 1,10; x2 = 0,910.

Далее в формулах (7.58)—(7.60) остаются неопределенными величины о0 и Ь. Для их определения имеем условия:

ф(6)= 1;

«г1* («і) +1 «г2) («) I = аетр).

Первое из этих условий в соответствии с (7.40) в нашем случае напишется в виде

[а<2> (b)f - [о<2> (6)] [о? (6)1 + К2) (b)f = as-

Подставив сюда значения a<2> (b), о<2> (Ь) по формулам (7.59), получим

vs 4-aoexpjsp, (4 у2 [(4)к' - 1] +

-ьзр2 [(-гГ-1]}==а«- (7'64)

Если иметь в виду соотношения (7.23) и (7.58), второе из усло­вий (7.63) даст

г / 6 xx. iv»

1 - L її / h 6и I In) I

х ехрізрх (4 у* [(4)*‘-1] +зр2 [(4Г~ 1]}=е"

Подставив сюда значение а0 из (7.64) получим уравнение для определения радиуса пластической зоны Ь:

, 1 +И / <2~ Ч"*У/г <Р1~Рд) _ ^ЕегР) /7fiC4

^ | _ Ц (р^ 2 (2 _г]игр«і),/г Pi (1 — p)as’

(р)

где

Последнее при E = 2-10® кГ/см2; a5 = 4050 кГ/сма; p = 0,3;

= 1,21; p2 = 1,10; Kj = 0,826; >ca = 0,910; a = 2 слц d = = 2,6 cm; cc = 125-10-7; TK — 7"0 = 600° С вместе с (7.64) дает b = 3,42 см а0 = 4910 кГ/см2.

Зная величины b и с0, по формулам (7.23), (7.58)—(7.60) можно построить кривую ег радиальных деформаций. Нетрудно при этом уточнить интервал изменения переменной t. По формулам (7.58) имеем

|&-*-»(4 г (-гГ-».»«■

Таким образом, в рассматриваемой нами задаче переменная t из­меняется в интервале

—2 < / < —0,884.

Полученные здесь результаты показывают, что учет упрочне­ния металла в кольце а ==£ г ==$ d дает значительное увеличение

напряжений (сг0 на 11%), увеличение радиуса упруго-пластиче­ской зоны b на 4% и, как показывает рис. 24, где нанесены соответ­ствующие значения ег (кривая 2), приводит к увеличению радиаль­ной деформации ег в пластических зонах. Вместе с удалением от г = а ег значения, полученные с учетом упрочнения, сближаются со значениями, полученными без учета упрочнения и это сближение практически завершается вблизи внутренней границы наружной упругой области. Таким образом, учет упрочнения металла в кольце a^r^d не приводит к нужному сближению эксперименталь­ных и теоретических значений ег вблизи внутренней границы наружной упругой области, и, следовательно, уточнение решения, полученного в предыдущем параграфе, должно быть проведено главным образом за счет учета пластических деформаций нагрева зоны, где в предельном состоянии нагрева Т Тк.

Учет пластических деформаций нагрева зоны, где в предельном состоянии Т ^Тк

Как было указано выше, второй причиной указанного расхо­ждения между опытными и теоретическими значениями радиаль­ной деформации должны являться неучтенные основной гипоте­зой пластические деформации тех частей листа, которые в пре­дельном состоянии нагрева находятся вне изотермы Т — Тк. Для точного учета этих пластических деформаций необходимо знать закон их изменения вне изотермы Тк. При подвижном источнике, создающем пространственное поле, этот закон неизвестен. Поэтому приходится искать пути их приближенного учета. Можно, напри­мер, предложить следующие простые способы учета этих пласти­ческих деформаций.

Первый способ. Для простоты можно принять, что пласти­ческие деформации нагрева вдоль прямой, нормальной к оси шва и к изотермической поверхности Тк предельного состояния на­грева, вне изотермы Тк изменяются по линейному закону, обра­щаясь в нуль на некоторой изотермической поверхности Ту. Другими словами, если обозначим через Тк цилиндрическую по­верхность, через Тк — огибающую изотермической поверхности, а через Ту — концентрическую с ней цилиндрическую поверх­ность, на которой вдоль указанного перпендикуляра пластические деформации нагрева равны нулю, то принимается, что между по­верхностями Тк и Ту пластические деформации изменяются по линейному закону. Этот способ учета пластических деформаций нагрева, где Т с Тк, удобен при применении первого метода. При применении второго метода можно использовать дальнейшее упрощение и принять, что все элементы, оказавшиеся внутри поверхности, являющейся средней между цилиндрическими по­верхностями Тк и Ту, в предельном состоянии нагрева получат активную пластическую деформацию сжатия а (Тк — 7%) в тех

направлениях, в которых температурное расширение было не­свободно. Это упрощение оправдывается тем, что при применяе­мых на практике режимах сварки, особенно при больших скоро­стях сварки (например, при автоматической), длина отрезка ука­занной прямой между поверхностями Тк и Ту мала по сравнению с характерными размерами свариваемых изделий, которые обес­печивают их жесткость [103]. В общем случае для нахождения изотермической поверхности Ту, на которой пластические дефор­мации нагрева в предельном состоянии равны нулю, необходимо найти температурное поле предельного состояния нагрева для рассматриваемого случая (гл. 2) и решить соответствующую за­дачу термоупругости (гл. 3). Для простоты в первом приближе­нии Ту можно найти из условия

es = a(Ty — T0), (7.66)

где es — пластическое относительное удлинение на условной гра­нице текучести.

Второй способ. Для простоты можно принять, что в предель­ном состоянии нагрева активную пластическую деформацию сжа­тия а (Тк — Т0) в направлениях, в которых температурное рас­ширение было несвободно, получат все элементы, оказавшиеся внутри изотермической поверхности-, определяющей границу из­менения механических свойств основного металла. Этот способ учета пластических деформаций нагрева зоны, где Т <С Тк, можно использовать как при применении первого метода, так и при при­менении второго метода.

Переходя теперь к нашей задаче с листом, отметим, что в этом случае в предельном состоянии нагрева будет существовать не­которое кольцо а ^ г sg: с, где температура нагрева, будучи меньше Тк, всюду больше или равна (на г = с) тому ее значенню, при котором появляются пластические деформации из-за несво­бодное™ температурных деформаций нагрева.

Если известна температурная кривая Т (г) предельного со­стояния нагрева, то решая соответствующую упруго-пластическую задачу [64], можно найти температурные напряжения or (Т), ае (7). Тогда наружный радиус с указанного кольца найдется, например, из условия

[о, (Г)]2 _ о,(Т)ав(Т) + [о. (Г)]2|г=с = а2(Т) г=с. (7.67)

Расчеты показывают, что это кольцо будет включать в себя кольцо а г ^ d зоны переходной структуры, где основной ме­талл в результате нагрева и остывания получил структурные из­менения и изменения механических свойств. Для учета пласти­ческих деформаций кольца а ^ г ^ с можно использовать, напри­мер, приближенный второй способ, т. е. принять, что круг г = d, включающий всю область, где в результате нагрева и последую­щего остывания произошли структурные изменения и изменения механических свойств металла, в предельном состоянии нагрева получил пластическую деформацию сжатия

е<р) = а(Тк-Т0). (7.68)

В этом случае из уравнений (7.35) и (7.36), подставив d вместо а, получим:

сг0 = 4525 кГ/см2; b = 4,3 см,

т. е. а о остается неизменным, увеличивается лишь наружный радиус пластической зоны. По формулам (7.37) можно найти ра­диальные деформации ег в отдельных зонах, соответствующие этим значениям о0 и Ь. На рис. 24 нанесена кривая ег (кривая 5), по­лученная путем указанных расчетов. Непосредственно видно, что учет пластических деформаций нагрева, где в предельном состоя­нии нагрева Т ■< Тк, правильно дополняет решение задачи, полу­ченное на базе основной гипотезы — получается удовлетворитель­ное совпадение теоретических и экспериментальных значений ра­диальной деформации.

Результаты, приведенные в п. 30, 31, полностью подтверждают правомерность основной гипотезы. Они показывают, что прибли­женные значения деформаций и напряжений, вызываемых после мощного сосредоточенного нагрева и последующего остывания, в том числе и приближенные значения сварочных деформаций и напряжений, определяются величиной а (Тк — Т0).

Для фактического определения приближенных значений свароч­ных деформаций и напряжений можно использовать или аппарат температурной задачи, где закон распределения температуры охла­ждения определяется законом распределения пластических де­формаций нагрева (первый метод, п. 29), или же метод сшивания (второй метод, п. 29). Оба эти метода позволяют учесть изменение механических свойств основного металла зоны шва в результате сварки и остывания и в каждом конкретном случае дают один и тот же результат. В зависимости от теплофизических характе­ристик основного и наплавленного металла, режима сварки и жесткости свариваемых элементов после сварки и остывания изде­лие может оказаться или в упругом или в упруго-пластическом деформированном состоянии [20, 65]. Независимо от этого, даже в случае плоской задачи, определение приближенных значений сварочных деформаций и напряжений по существу сводится к ма - кродислокационным задачам, более сложным, нежели дислокации Вольтерра [68].

Решения, полученные на базе основной гипотезы тем или дру­гим из этих двух методов, могут быть уточнены путем учета пла­стических деформаций нагрева тех частей изделия, которые в пре­дельном состоянии нагрева находятся вне изотермы Тк. Для приближенного учета этих пластических деформаций нагрева реко­мендуется два простых способа уточнения (п. 31). Первый из них является более общим, а второй применим лишь в тех случаях, когда сварка вызывает изменения механических свойств основ­ного металла зоны шва.

Таким образом, размеры зон активных пластических дефор­маций нагрева не назначаются автором (см. работу [18], стр. 225), а определяются основной гипотезой и приближенными методами учета пластических деформаций нагрева зон, где в предельном состоянии нагрева Т <■ Тк. Основная гипотеза предусматривает определения изотермической поверхности Тк предельного состоя­ния нагрева при сварке изделия из данного металла при заданном режиме сварки. Эта поверхность и ее огибающая могут быть най­дены теоретически или экспериментально. Наиболее общий спо­соб уточнения (первый способ) требует нахождения изотермиче­ской поверхности Ту и ее огибающей, которые могут быть найдены теоретически или экспериментально. Если эти огибающие поверх­ности Тк и Ту найдены, то для определения остаточных сварочных деформаций (напряжений) можно использовать первый метод или второй, которые сводят эту задачу к обычной задаче исследования упруго-пластических деформаций.

Рассмотрим теперь применение этой теории к решению кон­кретных задач. При этом мы будем пользоваться как первым ме­тодом, так и вторым методом при первом или втором способах уточнения в зависимости от того, какой из этих двух методов бы­стрее приводит к цели, но во всех случаях с обязательным учетом истинного или усредненного упрочнения металла зоны шва.

11 Г. Б. Талыпов