СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
ОСНОВЫ ПРИБЛИЖЕННОЙ ТЕОРИИ СВАРОЧНЫХ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ
ОСНОВНЫЕ ДОПУЩЕНИЯ И ГИПОТЕЗЫ
Предлагаемая приближенная теория сварочных деформаций и напряжений для металлов рассматриваемого класса базируется на следующих допущениях и гипотезах.
1. Рассматривается металл, который резко теряет свою способность сопротивляться пластическим деформациям в определенном для него достаточно узком интервале температур. Для простоты принимается, что он теряет способность сопротивляться пластическим деформациям при определенной средней в этом интервале температуре Тк.
2. При сварке имеет место мощный сосредоточенный нагрев подвижным источником весьма ограниченной зоны изделия до температур Т 3; Тк. В каждом конкретном случае огибающая подвижной изотермической поверхности Тк предельного состояния нагрева может быть найдена опытом или же методом, разработанным академиком Н. Н. Рыкалиным (гл. 2).
3. При установившемся режиме ручной и автоматической сварки ширина зоны термического влияния как линейного шва, так и любого из пересекающихся швов, а также механические характеристики металла этой зоны вдоль линий, параллельных оси шва, по длине шва остаются постоянными.
4. Структурные изменения основного металла, изменения его механических свойств, а также деформации (напряжения), возникающие в результате мощного сосредоточенного нагрева элемента достаточной жесткости, свободного от макронапряжений, и его последующего остывания, определяются разностью Тк — Т0.
5. Если подвергнуть мощному сосредоточенно-равномерному по толщине нагреву неподвижным источником ограниченную внутреннюю часть достаточно большого плоского листа, имеющего начальную равномерную температуру Т0, так, чтобы температура в этой ограниченной области удовлетворяла условию Т ^ Тк, то к моменту выравнивания температуры до Тк внутри изотермы Тк при остывании (после удаления источника) часть листа, содержащаяся внутри изотермы Тк, получит пластическую деформацию сжатия, главное значение которой определяется величиной а (Тк — 70), где а — среднее значение коэффициента линейного расширения в интервале 7„ ^ Т ^ Тк. Из-за стесненности температурных деформаций во время последующего остывания величина а (Тк — Т0) в основном определяет деформации и напряжения листа после его полного остывания. Это положение мы называем основной гипотезой. Она определяет величину активной части пластической деформации зоны интенсивного нагрева в первом приближении[5].
Для нахождения соответствующих значений деформаций (напряжений) изделия после его остывания могут быть использованы следующие два метода.
Первый метод. В момент выравнивания температуры до Тк внутри поверхности Тк при остывании изделие принимается сплошным и свободным от напряжений. Последние в основном возникают в результате остывания от Тк до Т0 его части, содержащейся внутри поверхности Тк и получившей при нагреве активную пластическую деформацию сжатия а (Тк — Г0). Поэтому задачу определения сварочных деформаций (напряжений) в первом приближении можно свести к некоторому классу температурных задач деформируемого тела, где закон распределения температуры охлаждения ограниченной зоны изделия определяется законом распределения активных пластических деформаций нагрева той же зоны при сварке. При нагреве центра листа задача определения этих деформаций (напряжений) сводится к определению деформаций (напряжений ) того же листа, возникающих при его охлаждении в соответствии с законом;
т = - г=~(тк-т0);
a sg г оо; 7 = 0,
где а — радиус изотермы Тк.
Второй метод. К моменту выравнивания температуры до Тк внутри поверхности Тк при остывании часть изделия, ограниченная этой поверхностью, получает активную пластическую деформацию сжатия а (Тк — Т0) в тех направлениях, в которых при нагреве стеснено температурное расширение. Если в этот момент указанную часть отделить от изделия, то к моменту остывания до начальной температуры 70 она получит относительное уменьшение своих размеров на величину а (Тк — 70) в направлениях, в которых было стеснено температурное расширение при нагреве, а остальная часть изделия принимается свободной от напряжений и имеющей равномерную температуру 70. В соответствии с этим в общем случае задача определения приближенных значений сварочных деформаций и напряжений, возникающих в результате наложения валика на поверхность тела, имеющего равномерную
температуру Т0, вдоль некоторой линии L, сводится к определению деформаций и напряжений тела, получающегося в результате сшивания двух тел с равномерной температурой Т0. Одно из этих тел получается из исходного путем последовательного удаления от него всех элементов, оказавшихся внутри изотермической поверхности Тк предельного состояния нагрева при перемещении источника по линии L из начального положения А в конечное положение В, а другое из них образовано элементами, оказавшимися внутри поверхности Тк предельного состояния нагрева и получивших к моменту выравнивания в них температуры до Тк при остывании пластическую деформацию сжатия а (Тк— Т0) в тех направлениях, в которых температурные деформации нагрева были несвободны. Если S — поверхность сшивания, v — нормаль к этой поверхности в некоторой ее точке с радиусом-вектором р, К(1), Е(2) — векторы смещения соответствующих точек поверхностей тел 1 и 2 при сшивании, а и (3 — криволинейные координатные оси на той же поверхности, образующие вместе с направлением v ортогональную систему координат, то условиями сшивания указанных двух тел будут:
а(1) — о(2)-
Tpv — Tpv,
Vw-Vl2) = kpa(TK-T0),
где k = 1 для тех из направлений а, р, v, в которых при сварке были стеснены температурные деформации; k = 0, если в данном направлении эти деформации не были стеснены.
Аналогично может быть сформулирована задача определения приближенных значений сварочных деформаций и напряжений в случае многосвязного тела. В случае нагрева в центре листа эти деформации и напряжения могут быть найдены путем сшивания листа с круговым отверстием радиуса а с круговым диском радиуса йа = а [1 — а (Тк — Т0)].
Эта основная гипотеза справедлива во всех случаях, когда размеры изотермы Тк предельного состояния нагрева малы по сравнению с теми размерами свариваемых элементов, которые обеспечивают их жесткость, стесняя температурное расширение зоны интенсивного нагрева. Применимость предлагаемой теории ограничена этим классом задач. Но указанное ограничение, если иметь в виду, что при сварке имеет место нагрев до Т ^ Тк весьма ограниченной зоны изделия, не суживает практическую применимость этой теории. Действительно, при используемых на практике режимах сварки полуширина изотермы Тк не превосходит 3—4 см (см. стр. 79—83 в работе [1031), а при больших скоростях сварки (при автоматической сварке) она и того меньше, в то время как
длина изотермы Тк, при условии наличия жесткого металла спереди и сзади, не может оказать влияния на сварочные деформации и напряжения.
|
Рис. 20 |
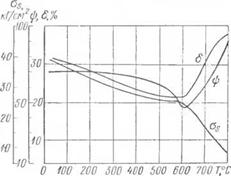
Положение 1 является схематизацией общеизвестного опытного факта, а также используется и другими авторами [76, 83]. Такого рода схематизация нередко применяется в механике деформируемого тела (например, схемы упруго или жестко-идеально пластических тел) и себя оправдывает. Для рассматриваемой в настоящей работе стали типа СХЛ зависимости ст8, б, ф от температуры Т, полученные на основе проведенных нами опытов, даны на рис. 20. Положение 2 базируется на работах Н. Н. Рыка - лина, подтвержденных опытами в работе [103].
Положения 3, 4 базируются на изложенных в п. 23—25, 27, 28 данной работы автора. Правомерность положения 5 (основной гипотезы) доказывается ниже в п. 30 путем сравнения теоретических результатов, полученных на базе основной гипотезы, с результатами опытов по сосредоточенному нагреву средней части полосы с заделанными концами и внутренней части большого плоского листа. Основная гипотеза в определенном смысле развивает идеи работы [93], где введены функция упругой усадки х и полуширина зоны усадки X, знание которых позволяет авторам [93] найти упругое решение соответствующей задачи.
В каждом конкретном случае и и % находятся путем измерений соответствующих размеров деталей до сварки и после сварки и вырезки.
Как указано выше (и. 29), эта гипотеза утверждает, что главное значение активной части пластических деформаций при сосредоточенном равномерном по толщине нагреве ограниченной внутренней части большого плоского листа определяется величиной а (Тк — Т0) в тех направлениях, в которых температурное расширение при нагреве было не свободно. При сосредоточенном равномерном по ширине и толщине нагреве средней части длины полосы с жестко заделанными концами температурное расширение будет стеснено главным образом в направлении оси полосы. Деформации и напряжения, возникающие в направлении оси полосы после такого нагрева и остывания, можно рассматривать или как поперечные для короткой пластины с заделанными продольными краями, или как продольные для полосы с заделанными концами. Пр и
сосредоточенном равномерном по толщине нагреве неподвижным источником ограниченной внутренней части большого плоского листа температурное расширение будет стеснено в радиальных направлениях. В результате такого нагрева и остывания возникает плоское поле остаточных напряжений. Из этой гипотезы следует, что при подвижном источнике все элементы в момент их выхода из подвижной изотермической поверхности Тк будут иметь активную пластическую деформацию сжатия а (Тк — Т0) в тех направлениях, в которых температурное расширение при нагреве было не свободно.
В дальнейшем (гл. 8) основная гипотеза и предложенные способы приближенного учета пластических деформаций зон, где в предельном состоянии нагрева Т -< Тк (п. 31), используется для теоретического определения остаточных сварочных деформаций и напряжений в сварных соединениях. Для ряда задач дается опытная проверка расчетных значений остаточных сварочных деформаций и напряжений, которая показывает, что приближенная теория дает удовлетворительные количественные результаты.