СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
МЕТОДЫ, ОСНОВАННЫЕ НА ПРИМЕНЕНИИ АППАРАТА ТЕМПЕРАТУРНОЙ ЗАДАЧИ ДЕФОРМИРУЕМОЙ СРЕДЫ
Метод Boulton и Lance Martin
Авторы [139] исходят из результатов проведенных ими опытов по замерам деформаций полос, на продольные кромки которых наплавлялись валики. Эти опыты показали, что как при наплавке валика на одну из продольных кромок, так и при одновременной наплавке валиков на обе продольные кромки, имеет силу
гипотеза плоских сечений для полос с отношением длины к ширине
;=s 17,7. Как и в работе [11], эта гипотеза положена в основу
метода [139]. Для нахождения закона распределения температуры но ширине поперечного сечения полосы в любой момент времени авторы используют известное решение задачи о температурном поле [48] пластины, по одной из граней которой перемещается с постоянной скоростью источник заданной мощности. При нагреве и последующем остывании предполагается наличие зоны пластических деформаций. Используя зависимости между напряжениями и деформациями в упругой и упруго-пластической зонах с учетом температурных членов и используя гипотезу плоских сечений, можно найти деформации и напряжения в поперечном сечении полосы в любой момент времени. Так как сварочные деформации и напряжения полосы определяются пластическими деформациями того состояния нагрева, где ширина зоны пластических деформаций является наибольшей, авторы 1139] отдельно рассматривают момент предельного состояния нагрева, момент наибольшего проникновения пластических деформаций нагрева О ^ у ^ ух и момент полного остывания. В момент наибольшего проникновения пластических деформаций нагрева (момент tx) продольные деформации в упругой зоне определяются соотношением
|
|
(5.1)
Если ev и е2 — относительные деформации продольных волокон у і и у — Ь, то, используя гипотезу плоских сечений, получим
С1 g2 е g2 /Г
Ь-Уі - ь-у ’ (b'z)
которое вместе с (5.1) дает
|
|
(5.3)
Каждое волокно зоны пластических деформаций 0 ^ у «S у і может иметь максимальную температуру, которая выше его температуры в момент наибольшего проникновения. Для каждого такого волокна в момент наибольшей температуры можно использовать соотношение
|
|
(5.4)
где asm, Ет — соответственно предел текучести и модуль упругости при максимальной температуре данного волокна.
После достижения максимальной температуры начнется остывание данного волокна, и в момент tx последующего остывания его деформация определится формулой
|
|
Приращение деформации за рассмотренный период остывания определится соотношением
Основываясь на собственных проведенных расчетах, авторы [139] принимают, что разность (е — ет) мала по сравнению с величиной (атТт—ar. Tj). Тогда соотношение (5.6) для напряжений пластической зоны дает
оТ =ЕТ (-тР - + а Т —атТ.), (5.7)
Т, Ет 1 т т Т, 1) ’ V '
если правая часть меньше а„г, и о*Гі = as7-i, если правая часть больше asn.
Неизвестные величины ег и є2, входящие в соотношение (5.3), определяются из условий равновесия внутренних сил в данном поперечном сечении полосы:
TOC o "1-5" h z Уі ь
|
О - У1 |
j °хт dy + | вхт dy = 0;
(5.8)
J вхтУ dy + J GxTydy=xO,
0 у,
а величина уг находится из равенства
ахт(Уі) = а*тг (5-9)
Так определяются деформации и напряжения в упругой и пластической зонах в момент наибольшего проникновения.
При определении остаточных деформаций и напряжений после полного остывания авторы предполагают наличие зон упруго - пластических (0 ==£; у «S t/3) и упругих {у3<: у ^ Ь) деформаций. Если ах — остаточные напряжения в упругой зоне, то изменение относительных деформаций в упругой зоне с момента t1 до момента полного остывания определится формулой
e = - J— - р— аг. гі» Уг^У^Ь> (51°)
а в пластической зоне имеет место равенство
(У) = os, О^у^уз.
Обозначив через е3 и е4 относительные деформации продольных ВОЛОКОН у = Уз, у = b и использовав гипотезу плоских сечений, получим:
ё = Т^(Ь~У) + еь (5.11)
|
|
|
|
|
Для определения величин еэ и е4 можно использовать уравнения равновесия (5.8), а у3 находится из равенства |
с* (/Уз) = Os-
Авторы [139] в своей работе дают сравнение теоретических значений остаточных напряжений, полученных изложенным здесь способом, с их опытными значениями. Это сравнение показывает их удовлетворительное соответствие.
Дальнейшее свое развитие это направление получило в работах [76, 85, 86].
Второе направление в разработке теории сварочных деформаций и напряжений развивалось также в работах ряда других авторов. С. А. Кузьминов [55] развил метод Н. О. Окерблома применительно к судовым конструкциям. Н. С. Лейкин [60] рассмотрел задачу о деформациях и напряжениях в точках листа, возникающих при нагреве его внутренней круговой области, как температурную задачу теории упругости. О. А. Бакши [7] рассмотрел ту же задачу с учетом пластических деформаций без опытной проверки и получил те же результаты, что и Н. С. Лейкин [60]. С целью выяснения механизма трещинообразования при сварке пластин, К. П. Большаков [10] применил аппарат плоской задачи теории упругости к определению временных температурных напряжений (деформаций) для той же задачи. Он рассмотрел также случай подвижного поля напряжений в тонкой бесконечной пластине, когда соответствующая изотерма Тк имеет форму овала. Используя конформное отображение внешности изотермы Тк на внешность окружности единичного радиуса и применяя аппарат плоской задачи, он нашел временные напряжения. В работе [10] не учитываются пластические деформации, возникающие в процессе сварки, и не рассматривается вопрос об остаточных деформациях и напряжениях. В последующем некоторые задачи термоупругости для подвижных источников тепла были рассмотрены в работах [18, 92].
В. С. Игнатьева [42] рассмотрела задачу о временных напряжениях свариваемых встык пластин при условии, когда шов накладывается одновременно на всю его длину. В этой работе сначала изучается плоское упругое деформированное состояние пластин и устанавливается, что третье главное напряжение Zz мало. Затем изучается плоское напряженное состояние этих пластин в пределах упругости. Для исследования упруго-пластических деформаций пластин рекомендуется метод упругих решений А. А. Ильюшина |44]. Остаточные напряжения автор [421 рекомендует определять на основе того, что они «в первом приближении равны по величине и обратны по знаку напряжениям,
возникшим в момент исчезновения зоны термопластичности». Это положение, полученное И. П. Байковой [4], приближенно справедливо для случая линейного напряженного состояния (для свободной полосы) и, как нетрудно убедиться, оно не распространяется на плоское и пространственное напряженное состояние.
Упрощенный метод Г. А. Николаева [74—76]
Основной недостаток теории [139] заключается в том, что она не учитывает наличия зоны, где температура нагрева выше температуры, при которой металл теряет свою способность сопротивляться пластическим деформациям. Этого недостатка нет в методе, предложенном Г. А. Николаевым. Проверив на опыте справедливость гипотезы плоских сечений при наложении валика на продольную кромку узкой пластины, автор [76] впервые разграничивает зоны чисто пластических, упруго-пластических и чисто упругих деформаций. Если распределение температуры по данному поперечному сечению пластины в данный момент времени определяется функцией Т = Ф (у), то относительные температурные удлинения продольных волокон определяются соотношением «Ф (у). В силу гипотезы плоских сечений продольные деформации пластины определятся не кривой аФ (у), а некоторой прямой. Поместим начало координат в точке свободной кромки и ось оу направим к наплавленной кромке. Крайние ординаты указанной прямой обозначим через у (0) = О'т', у (b) — От. Ординаты точки той же прямой на расстоянии у от начала у координат обозначим через р, где
|
(5.12) |
о'т’Ь + у (от — о’т’)
Напряжение в продольном волокне у определится соотношением
|
(5.13) |
о = Е [аФ (у) — р.
Допустим, что пластинка в рассматриваемый момент находится в упруго-пластическом деформированном состоянии. Ширину упругой зоны обозначим через с. Напряжение во всех точках пластической зоны (Ь — с) принимается постоянным и равным пределу текучести os. Тогда для определения величин От и О'т', входящих в формулы (5.12) и (5.13), можно использовать уравнения равновесия внутренних сил:
С
[аФ(у) — p]dy--o,{b — с) = 0;
SHAPE * MERGEFORMAT

|
О |
|
С |
(5.14)
Е J [аФ (у) - р]у dy + ~y~ (fc2 - с2) = 0
О
|
(5.15) 81 |
и добавочное условие
Е [аФ (с) — рс] = os.
6 Г. Б. Талыпов
После охлаждения в зоне (b—с) возникают пластические деформации
ер = аФ (y) — es — p, (5.16)
где es =
Действительные деформации после остывания будут определяться гипотезой плоских сечений. Обозначим крайние ординаты соответствующей прямой линии через у (0) = О-'п', у (Ь) = Oil. При этом остаточные напряжения определятся формулой
а = ЕаФ (у) — as.— рЕ — р'Е, (517)
где
р'= О'п'Ь + УУп-О'п') ' (5 )8)
Величины On и 0'п' определятся из уравнений равновесия внутренних сил:
ь ь
Е | [аФ (у) — es — p]dy — Е p'dy = 0;
о
|
ь |
(5.19)
Е J [аФ (у) es р] у dy — Е p'ydy=: 0.
Таким образом, видим, что рассмотренный метод позволяет определить как временные, так и остаточные деформации (напряжения). Следует также отметить, что автор [761 подчеркивает применимость этого метода лишь к узким пластинкам, для которых имеет силу гипотеза плоских сечений. Результаты проведенных опытов [76] показали, что для широких пластин эта гипотеза не применима.
Метод учета дополнительных пластических деформаций нагрева, возникающих после предельного состояния
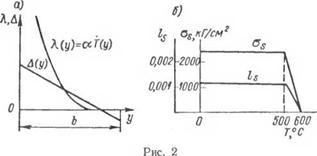
Изучая свободные и несвободные деформации прямолинейных стержней при их равномерном нагреве по длине и при таком же равномерном последующем охлаждении, Н. О. Окерблом предлагает «рассматривать отдельные продольные волокна неравномерно нагретой полосы, как равномерно нагретые стержни с ограниченной свободой перемещения» (см. стр. 33 в работе [85]). Если, например, для некоторого сечения х полосы распределение температуры по ширине представлено кривой Т (у) (рис. 2, а), продольные волокна этой полосы в предположении, что они не связаны друг с другом, получают относительные тепловые удлинения, определяемые кривой "К (у) (рис. 2, а). Но действительные деформации каждого продольного волокна, как отмечает автор, зависят от деформаций всех других продольных волокон, причем «для деформации полосы с достаточной для практики точностью
можно признать справедливой гипотезу плоских сечений. . .», в силу чего «действительные деформации изобразятся не кривой Я (у), а прямой Д (г/)» (рис. 2, а). Так как действительная деформация Д (у) каждого волокна отличается от свободных температурных деформаций Я (у), то величиной разности 1Д (у) —Я (у) I определятся растягивающие или сжимающие напряжения в поперечном сечении данного волокна по формуле
охх = Е [Д (у) — Я (у)] = Еехх (5.20)
в зависимости от того, каков знак этой разности. При этом деформации во всех волокнах будут упругими, если для любого
|
|
из них ехх < es. Если же для некоторой группы продольных волокон ехх < es, то в этих волокнах будут иметь место упругие деформации, равные es, и пластические деформации
е{р) (у) = ехх — es. (5.21)
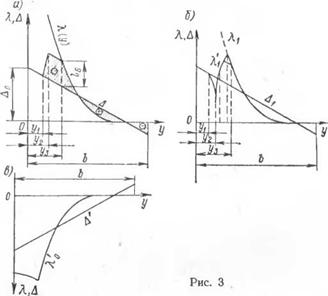
Если для зависимости между напряжениями и деформациями принять схему идеальной текучести для любой температуры в определенном для данного материала интервале, то эпюра напряжений в рассматриваемом сечении определится эпюрой упругих деформаций в том же сечении. Например, приняв для малоуглеродистой стали приведенные на рис. 2, б графики изменения предела текучести и относительных деформаций на пределе текучести при растяжении и сжатии в зависимости от температуры, автор получает эпюру упругих деформаций, представляемую заштрихованной на рис. 3, а фигурой. При этом на участке у3 ^ у ^ b имеют место только упругие деформации, так как для этого участка
|Л(0)-Ч0|<|е,|, (5.22)
и напряжения в продольных волокнах этого участка определяются по формуле
схх = Е[А(у)-Цу)]. (5.23)
На участке г/2 ^ У «S Уз. где 7" < 500° С, но | А (у) — Я (t/) | >
>|es|, имеют место и постоянные упругие деформации es, кото
рыми определяются постоянные напряжения
ахх = as (5.24)
и пластические деформации, определяемые соотношением (5.21). На участке ух ^ у ^ г/2, где 500° С «s Т ^ 600° С, имеют место упругие деформации es (Т), определяющие соответствующие напряжения
oxx = Ees(T) = os(T), (5.25)
|
|
и пластические деформации, определяемые соотношением (5.21). На участке 0 у «£ ух, где Т ^ 600° С, имеют место только пластические деформации, так как при этих температурах принимается es (Т) = 0. Если полоса свободна от внешних связей и к ней не приложены внешние силы и моменты, то должны быть выполнены условия равновесия:
ь ь
o„dt/ = 0 J аххуdy = 0. (5.26)
о о
Присоединив к этим уравнениям равенство
А (Уз) — Ь (Уз) = —<г*.
Н. О. Окерблом получил систему (5.14), (5.15), которая должна однозначным образом определить как положение прямой Д (у), так и величину у3, фиксирующую правую границу зоны пласти
ческих деформаций. В процессе нагрева в отдельных волокнах полосы возникают пластические деформации, которые отражаются на деформациях всех ее волокон при последующем остывании. Например, если все волокна в момент, когда их свободные температурные деформации определяются кривой К (у) и не свободные деформации в тот же момент определяются прямой Д (у) (рис. З, а), освободить друг от друга, то при последующем их охлаждении до температурной кривой Ту (у) (рис. 3, б) их свободные деформации определяются кривой
ЫУ) = Му) + е{р)(у), (5.27)
где величина е<р> включает свой знак. Но продольные волокна полосы не могут деформироваться независимо друг от друга, в силу чего их действительные деформации определяются прямой Д! (у) (рис. 3, б). При этом положение прямой Дг (у) определяется из уравнений (5.26), если в эти уравнения подставить значения ахх, выраженные через деформации, и во всех формулах
(5.20) —(5.26) величину К (у) заменить величиной Я і (у). Аналогично можно определить пластические и упругие деформации и напряжения для любого другого момента времени процесса остывания. Величина е(р) (у) сохранится неизменной для данного волокна до момента полного остывания лишь в том случае, если в процессе остывания это волокно не получит пластических деформаций. Если же в процессе остывания рассматриваемое волокно получает пластические деформации, то его остаточная
деформация к данному моменту остывания е<р> (у) выразится
как сумма е(р> (у) и тех пластических деформаций, которые оно накапливало в процессе охлаждения до этого момента. Кривая свободных температурных деформаций в данный момент определится формулой
й М = Ш+е1р)(у). (5-28)
В момент полного остывания, когда Ях (у) = 0, температурные деформации определятся соотношением
Му) = ё{ор)(у). (5.29)
В общем случае вместо рассмотрения температурных кривых в данном сечении для различных последовательных моментов времени остывания автор предлагает «рассматривать температурные кривые неподвижного температурного поля для некоторых сечений, выбранных таким образом, чтобы они располагались на таких расстояниях от сварочной дуги, какие в действительности были в интересующие нас моменты времени между дугой и заданным сечением». В тех случаях, когда необходимо определить только остаточные напряжения, за первое сечение позади дуги, деформации которого отражаются на конечных результатах, автор берет сечение, перпендикулярное оси шва и проходящее через точку касания прямой, параллельной оси шва, с изотермой 600е С. Последующие сечения, указанные в вышеприведенной цитате, рекомендуется брать так, чтобы более полно охватить зону нагрева за первым сечением.
Применение этого метода к определению остаточных деформаций и напряжений в данном поперечном сечении полосы с учетом всех температурных состояний нагрева и остывания связано с необходимостью выполнения большой вычислительной работы, так как оно «потребовало бы рассмотрения очень большого количества последовательных моментов остывания» (см. стр. 38 в работе [85]). Поэтому Н. О. Окерблом вместо рассмотрения суммарной пластической деформации е<*>> (у) рекомендует использовать лишь «наибольшую пластическую деформацию сжатия», имеющую место в предельном состоянии нагрева. При этом свободные температурные деформации к моменту полного остывания определяются кривой
М У) = е(р)(у), (5.30)
а действительные деформации всех этих продольных волокон определяются прямой А' (у) (рис. 3, в), положение которой определяется из системы уравнений, аналогичной системе (5.26). Следует подчеркнуть, что, если не учитывать накапливающиеся в процессе остывания после предельного состояния пластические деформации, этот метод по существу идентичен рассмотренному выше методу Г. А. Николаева.
Необходимо отметить, что Н. О. Окерблом [83, 85, 86] не дает опытной проверки результатов, получающихся расчетным путем по его методу. Н. О. Окерблом, следуя допущению, что «наплавка валика на кромку полосы является тем случаем, который имеет особо важное значение, так как к рассмотрению деформаций и напряжений полосы, находящейся в тех или иных условиях, может быть сведена в конечном счете задача определения деформаций и напряжений для любых типов сварных конструкций и соединения», (см. стр. 49 в работе [85 ]), многие виды деформированного состояния, возникающие при сварке или в результате сварки, стремится свести к частному виду линейного деформированного состояния. Этот же тезис Н. О. Окерблом повторяет в другой форме в своих последующих статьях и монографиях, где рассматриваемый метод именует общей теорией сварочных деформаций и напряжений (см. стр. 3 в работе [83] и стр. 3, 4, 12 в работе [86]). Упомянутое допущение в некоторых случаях может привести к ошибочным результатам. Во избежание подобных ошибок в дальнейшем необходимо еще раз напомнить, что метод Н. О. Окерблома применим к определению сварочных деформаций и напряжений свободных полос, на деформации которых не наложены внешние связи и для которых имеет силу гипотеза плоских сечений. Вместе с тем этот метод не предусматривает учета необратимых изменений механических свойств основного металла зоны шва в результате сварки и остывания. В работах [63, 98] использованы ЭВМ для выяснения кинетики сварочных деформаций (напряжений) в поперечном сечении свободной полосы при наплавке валика на ее кромку на основе изложенного метода Н. О, Окерблома. Эти работы надо рассматривать как простейшие примеры применения машинного счета к простейшей задаче о сварочных деформациях.
За последние 10 лет появился ряд новых работ по исследованию сварочных деформаций и напряжений. В работах [18—20] рассматривается задача определения временных и остаточных деформаций и напряжений при местном нагреве неподвижным и подвижным источником бесконечной плоской пластины на основе теории малых упруго-пластических деформаций численным методом с применением ЭВМ. При этом необходимо иметь в виду, что металл определенной зоны при мощном сосредоточенном нагреве и остывании подвергается термическому сложному нагружению и использование к решению такого рода задач теории малых упруго- пластических деформаций не оправдано [117].
Более обоснованными являются алгоритмы численного решения плоской задачи термопластичности на основе теории пластического течения, разработанные в работе [65] применительно к сварке конечных прямоугольных пластин с заданными краевыми условиями. Последнее направление должно быть наиболее перспективным и его дальнейшая разработка должна проводиться путем сравнительного анализа расчетных и опытных значений сварочных деформаций (напряжений).
Глава 6