СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
ПРЕДЕЛЬНОЕ СОСТОЯНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА ПРИ ДУГОВОЙ СВАРКЕ
Подвижное температурное поле сосредоточенного источника постоянной мощности, движущегося прямолинейно и равномерно со скоростью v, с течением времени стремится к предельному квазистационарному состоянию. Это предельное состояние тео-
|
(2.38) |
|
4af |
|
/ |
|
6 = |
ретически устанавливается после бесконечно длительного действия источника. При сварке предельное состояние в области, близкой к источнику, устанавливается вскоре после начала процесса сварки [103].
Предельное состояние в случае полубесконечной области
|
|
|
£ 4at 4а |
|
R2 vH |
Подвижное температурное поле движущегося прямолинейно с постоянной скоростью точечного источника в полубесконечном теле с теплонепроницаемой граничной плоскостью определяется соотношением (2.30). Предечьное состояние наступает при t —> оо, т. е. для него получим
(2.39)
Вычислим этот несобственный интеграл. Для этого введем новую переменную
|
|
|
со
о |
При этом получим
|
с»
Я J Уц о |
где
|
|
|
2 |
|
|
|
Т] = |
|
оо |
|
оо |
|
о |
|
о |
ІІолагая
будем иметь
Известно [102], что
|
со
о |
и, следовательно,
При этом для исходного интеграла получим
|
J о |
«, R* vH. Г-— Rv
с Ш 4 а — ' 4flJt Р. 2 а
р/2 е R
и температурное поле предельного состояния определится соотношением
_ vx _ ^с'
T(R, х, оо) = 1^е~ ■-*»■*« . (2.40)
Если температурное поле неподвижно, то (2.40) при v = 0 даст
m*,o°)=2SR, (2.41)
т. е. в этом случае изотермическими поверхностями являются сферы с центром в источнике, температура изменяется обратно пропорционально расстоянию от источника и зависит также от мощности источника и коэффициента теплопроводности. Из (2.41) следует, что чем меньше коэффициент теплопроводности Я, тем шире зона нагрева.
При нагреве подвижным источником температурное поле в полубесконечном теле (2.40) зависит не только от расстояния от точки подвижного поля до источника, но и от положения этой точки относительно подвижной плоскости yz. В направлении перемещения источника (R = х, х |>0) температура определяется по формуле
Rv
т(«.«.“)= - Аїї'' “ • <2-42»
а в направлении, обратном направлению перемещения источника (х < 0),
Г (*.“*. оо)=2&- (2.43)
Сравнение последних двух выражений показывает, что наибольшие температуры и наименьшие градиенты температур имеют место позади источника.
Распределение температуры в плоскости yoz определится по соотношению (2.40) при х = 0, т. е.
_ Rv
7'<«.0.~)=2S«e 5°' <2-44>
Из (2.40) также ясно, что изотермическими поверхностями являются поверхности вращения относительно оси ох, сжатые со стороны положительных х, а также в направлении оси у. Пре
дельное состояние в полубесконечном теле с теплоотдачей на граничной плоскости определяется [103] соотношением
|
‘2ЛКК |
|
|
|
T(R, x,t) |
|
СО |
|
К 2nR |
|
о |
где
Г2 = X2 + у2
Д2 _ г2 + #
Интеграл в правой части последнего соотношения не выражается через табулированные функции и это затрудняет исследование температурного поля.
Предельное состояние в случае тонкой бесконечной пластинки
|
УХ 2 а со
о |
Подвижное поле для тонкой пластинки с теплоотдачей определяется соотношением (2.38). Предельное состояние наступит при / = оо и для него получим
(2.45)
Найдем значение несобственного интеграла. Для этого введем новую переменную
|
о
|
При этом получим
|
оо
|
где
По известно [102], что
|
со
о 3 Г. Б. Талыпов |
33
где/Со — функция Бесселя второго рода нулевого порядка. В силу этого (2.45) примет вид
ffc*. **('У4+-£)- <2-46>
Температурное поле предельного состояния в случае неподвижного линейного источника определится формулой
Т (г, =-sasr к„ (-■ У±) ■ (2.47)
Отсюда ясно, что изотермические поверхности в этом случае — круговые цилиндры высотой h с осью, совпадающей, с линейным источником. Вместе с удалением от источника температура убывает по закону убывания функции
к
стремясь к нулю при г —> оо. В случае подвижного линейного источника изотермы также представляют цилиндрические поверхности высотой h, нормальные сечения которых — замкнутые, симметричные относительно оси перемещения источника и вытянутые в направлении х < 0 кривые.
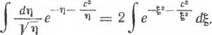 СВАРКЕ" title="ПРЕДЕЛЬНОЕ СОСТОЯНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА ПРИ ДУГОВОЙ СВАРКЕ" width="212" height="35 "/>
СВАРКЕ" title="ПРЕДЕЛЬНОЕ СОСТОЯНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА ПРИ ДУГОВОЙ СВАРКЕ" width="212" height="35 "/>