СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
НАПРЯЖЕНИЯ В БЕСКОНЕЧНОЙ УПРУГОЙ ПЛАСТИНЕ ОТ МГНОВЕННОГО ЛИНЕЙНОГО ИСТОЧНИКА
Многие задачи определения напряженного состояния решаются при помощи методов, разработанных в теории упругости. Ряд задач применительно к сварке при определенных допущениях
|
|
|
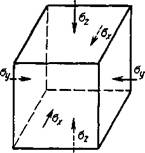
Рис. 11. Элементарный кубик из тела с напряжениями по |
|
граням |
|
— Ои — аг і аТЕ I — 2ц ' |
также может быть решен с использованием теории упругости. Рассмотрим общие положения метода.
|
ех = еу = ег — а Т |
Представим себе неравномерно нагретое тело, в каждой точке которого известна температура. Если бы частицы тела не были связаны между собой, то каждая из частиц беспрепятственно увеличилась в объеме. Выделим из тела элементарный кубик (рис. 11). Вследствие бесконечно малых размеров кубика неравномерностью температуры вдоль граней можно пренебречь и считать его равномерно нагретым до некоторой температуры Т. Составляющие деформаций кубика от нагрева до температуры Т будут равны
TOC o "1-5" h z Уху = Уух = Y« = °- (2)
Устраним эти деформации, приложив ко всем граням кубика напряжения сжатия, равные
аТЕ.
°, = °, = оІ=-ГГ2ІІ. (3)
То что напряжения (3) создадут деформацию, равную аТ, можно проверить, подставив их в уравнение (4), связывающее деформацию с напряжениями:
|
(4) |
= -є - [ох — В (оу + а*)].
Приложив к каждому элементарному объему соответствующие уравнению (3) напряжения, устраним полностью деформации от температуры. Затем «склеим» между собой все элементарные объемы. Напряжения на границах элементарных кубиков будут вычитаться, а разность этих напряжений создаст так называемые объемные силы. По границам тела, где напряжения не вычитаются, после «склеивания» кубиков будут действовать поверхностные
аТЕ
силы сжатия, равные 1 _ 2|1~ •
В действительности в нагретом теле никаких поверхностных и объемных сил нет. Поэтому полученные нами фиктивные поверхностные и объемные силы следует снять, приложив к телу силы противоположного направления. По поверхности тела следует приложить нормальные поверхностные силы
= Y = (5)
Внутри тела прикладывают объемные силы X, Y, Z, величину которых можно найти, если подставить напряжения (3) в дифференциальные уравнения равновесия (6), которые должны при этом у довл етво р я тьс я:
^Л-^ + ^ + Х=.0;
дх ду дг
до» дххи дх uz
|
(6) |
TOC o "1-5" h z Ъ + - ЗГ + 1*- + у = Ь
дог. дххг. fayz, 7 _ п
дг “Г дх + ду + ^ - а
С учетом того, что объемные силы прикладывают с противоположным знаком и что хху = хуг = хгх = 0, находим из уравнений (6)
X = — аЕ у - _ аЕ ?L. 7 - аЕ дТ
1 — 2ц дх ' I — 2|Л ' ду ’ ^ 1 — 2ц ' дг • (7>
Таким образом, напряжения, возникающие от неравномерного нагрева тела, складываются из трех составляющих:
1) так называемых гидростатических напряжений растяжения или сжатия по всем направлениям
аТЕ
при повышении температуры знак Т следует принимать положи - ьныи, при понижении — отрицательный;
2) напряжений, возникающих от поверхностных сил (5);
•j) напряжений, возникающих от объемных сил (7).
Решение задачи о распределении напряжений в неравномерно нагретом теле состоит в отыскании этих трех составляющих.
Для случая тонкой пластины, где напряжения ог равны нулю, составляющие напряжения имеют несколько иной вид:
1) гидростатические напряжения в плоскости
а ТЕ
1-ц •
2) поверхностные силы по краю пластины
X = Y = ~L. (9)
1 — (Л ' '
3) объемные силы
х = - т^г-1г; Y = - I~rw - <10)
Более подробные сведения о решении температурных задач можно найти в работах [110], [91]. Применим рассмотренный метод к определению напряжений в бесконечной пластине от мгновенного линейного источника тепла. Температурное поле от такого источника без теплоотдачи [100] описывается следующим уравнением
Найдем температурные напряжения в пластине в предположении, что металл является абсолютно упругим, а теплофизические и механические коэффициенты постоянны во всем диапазоне температур. Задачу будем решать в полярных координатах.
Составляющая гидростатического напряжения определяется просто по уравнениям (8) и (11):
Q-Eq dt 4at /іо
°'» = 0'« = -(Т=Й4ПШЄ • (12)
Температура на краю бесконечно большой пластины равна нулю. Поэтому поверхностные силы (9) также равны нулю и никаких напряжений в пластине не вызовут. Объемные силы (10), которые в полярных координатах запишутся как
D а Е дТ
* ~ — і _и, аГ»
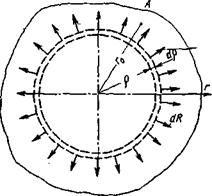
вызовут напряжения, для определения которых рассмотрим элементарную объемную силу dR — Rdp на расстоянии р от начала
координат и определим напряжения от этой силы внутри и вне круга с радиусом р (рис. 12):
а) внутри круга с радиусом р
|
(13) |
°гвн =
б) вне круга
__________________ J Р Рг л р.
|
(И) |
- 2 г2
О, J Р Р j п
*нар о - з
SHAPE * MERGEFORMAT

|
Рис. 12. Объемная осесимметричная сила di?, действующая на расстоянии р в бесконечной пластине |
|
|
|
1-М 2 |
Определим напряжения в точке А, находящейся на расстоянии г — г0> от всех объемных сил, действующих в пластине. Вначале найдем напряжение at от объемных сил, действующих внутри круга (г = г0). Для этого необходимо интегрировать выражение (14) в пределах от 0 до г0:
=
г0
aEaq di 2лЯвГп ^
--5. i+A
л 4at 4at
1
(15)
Объемные силы, действующие вне круга (г =/•(,), зызовут в точке А напряжения <т.
‘нар
|
(16) |
4д/
1 — р 8лЯ6/
'с
Суммируя напряжения (12), (15) и (16), находим
‘нар
|
1 4 at |
|
r0 4 at |
|
4a£ 'О |
|
1 — Є |
|
■2е |
|
(17) |
|
8лЯ6і |
|
~ at, + о, - fa, = ‘г і г ей 1 Ыар |
|
aEq dt |
Аналогично находим о/.
|
1 4а/ |
aEqa dt і,
0=---------- ч-—5- V 1 — Є
2 л). 6 г.
Если решать задачу с осесимметричным распределением температур Т в общем виде, то получим
С аЕ с
|
(19) |
°г = ^ -7г J Тг dr-
о. =~ - аГЕ + ^j' Trdr,
где С — произвольная постоянная, определяемая из краевых условий на наружном контуре пластины. Для бесконечной пластины С = 0.
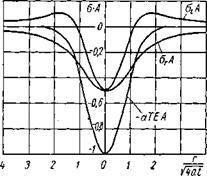
Проанализируем полученные результаты. На рис. 13 показаны кривые напряжений ог, at и —аТЕ в безразмерных значениях
|
Рис. 13. Распределение напряжений а, и d| п бесконечной пластине от мгновенного линейного источника тепла |
orA, atA; —аТЕА, где А —
п пп п
— -.. Величина —alb вы - аЬц at
ражает напряжения, которые возникают в стержне, нагретом до температуры Т, в случае жесткого закрепления его концов.
Обращает на себя внимание сложный характер распределения напряжений аг и otl который существенно отличается от характера распределения температур. Несмотря на то что во всех точках пластины произошел нагрев металла и, казалось бы, должны действовать только сжимающие напряжения, в пластине имеется значительная область с растягивающими напряжениями о). Максимальные напряжения при г = 0 в 2 раза меньше величины —а ТЕ. Это объясняется податливостью окружающего металла вследствие упругости по сравнению с абсолютно жестким его закреплением. Полученные результаты косвенно указывают на необходимость учета двухосности напряжений в случае сварочного нагрева и снижение напряжений вследствие упругости металла.