Механика трубопроводов и шлангов
Частные случаи параметрических колебаний шлангов, заполненных идеальной жидкостью
Свободные параметрические колебания прямолинейных шлангов. Рассмотрим наиболее простой случай параметрических колебаний шлангов, когда шланг имеет прямолинейную форму. Для большей физической наглядности рассмотрим уравнение параметрических колебаний в размерной форме. Уравнение параметрических колебаний прямолинейного шланга, заполненного идеальной жидкостью (/п=0), является частньщ случаем уравнений (35.19) — (35.20). В размерной форме записи уравнение свободных параметрических колебаний шланга имеет вид. д^и.. 9
(mi + т*) + 2 {w0+wx) — IQio - PqF — m2w0 — ptF—
— m2 (i2w(jw1-f - ®?)I -|-«o,} - = 0. (36.1)
В безразмерной форме уравнение (3.61) имеет вид
<?2М,- д2их 2
-|- 2пг (Щ + W,) 1<3ю — — «1+щ>01 X
№иг ди,.
X “Ь w0 — = 0, (36.21
De2 1 0 dr к '
Где Qio=Qii)--/3o — /zi®o - (36.3)
Ограничимся случаем, когда пульсирующие составляющие потока жидкости имеют вид (35.16) — (35.17).
Подставив в уравнение (36.2) выражения для Pi и Wi
(35.16) — (35.17), получим следующее уравнение: д2их ди
_i - + 2«>K+<% sin «зit) йГ+Ч.-й'—
— IQio— Рюо (1 — е) cos п-6% — пх sin nzx - j-
9 &Ur
-f-Wio sin2/^)] --- =0. (36.4)
В соответствии с изложенным в § 35 методом приближенного решения положим (ограничившись двухчленным приближением)
Ил-я=/х (т) sin ле - f-/2 (т) sin 2лє. (36.5)
Для функции /і и $2 получаем следующие уравнения:
/,+«іі/і+«12/2 bufi + *12/2=0; (36.6)
/2 + «2і/і + Й22/2 + ^і/і + ^2/2=0; (36.7)
Где
А12= —а2і=“" (™b+®w sin лз*)ї
Й 11 = ^22 == Ц)»
6,1=[Q10 — /J10D cos и3т — п! (2®,^! + ®?) - г Я, 00 cos n3tVi];
Ft,2= 4л2Я1(иcosя3ту2; Vi=j'E sinsпе</е=-І-; (36.8)
1B-j.
І sin 2яє-^е = —-
621 = n2P1(t(?COS fl3XУ2,
Й= 4л2 [Qit, — Я100 cos й3т — nx (2w0wx-fw?) + Я100 cos «3tv31 ; 1
Уч= в sin2 2лесіє=—.
Ограничившись главной областью параметрического резонанса, полагаем (первое приближение)
F і =а* sin cos —х,
У1 і 2 1 2
(36.91
/2=(22 sill-y-T-J-^COS
Подставив (36.9) в систему уравнении (36.6—36.7) после преобразований получим однородную систему алгебраических уравнений:
Cnai--cl2b1--clji2-]-CiAb2=Q
C2la 1 УС22^-~ С23а2 ~Ь ^24^2
(36.10)
Сзіаг і ^"зэ®2 С, ир2:= 0;
С41а1 +^42^1 - ht43tt2'f-^41^2 = 0.
Коэффициенты с*3- даны в приложении 8.
|
СМ |
![]()

|
0,24 |
![]()
|
3 6 8 12 п3 |
![]() Приравняв определитель системы (36.9) нулю, получим уравнение, связывающее а»ю и п3, где и я3 — координаты точек границы области устойчивости. Частный случай уравнения (36 4) рассмотрен в работе [68].
Приравняв определитель системы (36.9) нулю, получим уравнение, связывающее а»ю и п3, где и я3 — координаты точек границы области устойчивости. Частный случай уравнения (36 4) рассмотрен в работе [68].
|
О |
![]() Рассмотрим пример со следующими числовыми значениями размерных величин, входящих в безразмерные параметры исходного уравнения ма
Рассмотрим пример со следующими числовыми значениями размерных величин, входящих в безразмерные параметры исходного уравнения ма
Рис. 36.1
Лых колебаний (36.4): 4 м, £>==0,1 м; 6=3 10-3 м; пц=5 кг/м. т2=
=7,5 кг/м; С? ю(,)=1»5 10а Н. Шо-Ь м/с; ,Р==75 • 10~4 м2; р0== 1,2 10г' Н/м; 1010=1,5; 3 м/с.
Безразмерные параметры (при <3ю=<2ю(|)—Ро—л^о2) равны «1=0.6; 1^о=0,90; <3,0=0,66; «0=10-'; Я0=1,8; ш10=0,24; ш|О=0,48.
Если определитель системы (36.9) развернуть, то получим алгебраическое уравнение восьмого порядка относительно п3. Для каждого фиксированного аУ|о получаем (численным счетом) четыре действительных корня и два комплексно сопряженных Действительные корни соответствуют границам областей неустойчивости [двум областям, так как взято двучленное приближение (36.6), что соответствует представлению шланга как системы с двумя степенями свободы]. После вычислении получаем области неустойчивости (рис. 36.1), соответствующие главным параметрическим резонансам для первой и второй форм колебаний. Если учесть диссипативные силы, имеющие место в реальных системах, то области неустойчивости уменьшаются и опасные колебания становятся возможными только при более высоких значениях амплитуд переменных составляющих потока
На рис. 361 показана область (с двойной штриховкой) при учете сил вязкого трения с безразмерным коэффициентом а0= 10_|.
Параметрические колебания шланга относительно вертикальной плоскости. Уравнения малых параметрических свободных колебаний шланга относительно вертикальной плоскости получим как частный случай системы (35.19) — (35.20):
|
|
+ [р,+щ +®?)1 -5Г=°: (36'11}
<Зю=С}И’ - Р0- щт-МР. (36.12)
(36.12)
Основное отличие уравнения (36.11) от уравнения параметрических колебаний прямолинейного шланга заключается в том, что в (36.11) статическое натяжение @ю(,) переменно по длине шланга. Для шлангов, нагруженных только силами тяжести, натяжение (см. § 9)
|
|
Тде Сі и Сз' — произвольные постоянные, определяемые из условия закрепления шланга.
Воспользовавшись методом Б. Г. Галеркина, ищем решение уравнения (36.11) в виде
(36-14)
Где — собственные функции свободных колебаний шланга относительно вертикальной плоскости, метод определения которых изложен в § 32. Собственные функции Фз<'> удовлетворяют условию ортогональности:
U'»<f! K)*=0. (36.15)
О
Подставив (36.14) в уравнение (36.11), получаем систему неоднородных уравнений:
З (/= 1, 2,..., п (36.16)
О
Шли
Лц/х + Ьц/i - f... - J - biп/п + Сц/l + • - + clnfn— О, (36.17)
Hnnfn+ЬщА +... + Ы+Cmfi + - ■+ Cnnfn=0;
Где
Bij=2nl(w0--w1) (* - J - а0Вгі - j* <$il)de;
Cij={2w0W1--Wi) ^ срз(/)<Рзl)de-- ^ ^X
0 0 0
Х(4оЛ'^. (36Л8)
Ограничившись двучленным приближением, получаем сис
Тему уравнений:
Huf 1 bnf I - f - ^12/2 "Г Cnf 1 + Й2/2 = ^Ї (36.19)
^22/2 ~~ ^2і/г “Ь ^22/2"Ь ^21/1 “Ь ^22/2=О, где ^ 1
£п = 2/ij (и/оН-^і) f џ3(1,%l>^e - fa0 j
621 = 2и, (Я)0 + i«,) j 'Vf Л22 = 1<?32)?з2,Л;
K + a-J I <й%«»Л + afJ | -42>-fS2te;
%=JlQu?3(,,-№1(№(1Vlrf, Ve; C12= J IQnf3 —
C22 = j lVu'ft,* > — (Ql(ffa ^'Ifs^de,
[I — nlnlwvi(l— s) COS«3t+«, (2®УЩ110 sin n3t-|~OTi0 5in2/l3t).
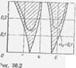 В качестве примера рассмотрим паоагет рическис колебания шланга, для которого в § 32 определялись частоты и формы при Р и wu соотпетствующпм (3516) и (35.17). Главные области параметрического резонанса для К||=9,Л 0.1 (при а.'0=0,6) приведены на
В качестве примера рассмотрим паоагет рическис колебания шланга, для которого в § 32 определялись частоты и формы при Р и wu соотпетствующпм (3516) и (35.17). Главные области параметрического резонанса для К||=9,Л 0.1 (при а.'0=0,6) приведены на
Рис 36.2.
Параметрические колебания шланга в вертикальной плоскости. При ис-
Пз следовании параметрических колебаний шлангов в вертикальной плоскости
можно использовав к г. к уравнения малых колебаний в неподвижных осях (30.20) - (30.21), так и уравнения в связанных осях (30 30) — (30 32). В неподвижных осях имеем четыре уравнения [частный случай системы (35.19) — (35.20)]:
И. д2 и с)их д~их д�х
^+2»1(«»+«4) «г+^-гг+^-лТ—зг=-
|
— г1- <*о ~ ~Ь — (?£С>Т ОТ ОЕ2 ДА(2*. : = п #*20 . dt 11 *2 5 ' ) А<?,. - Г-1—- LQ,, = 0; (36.22) —1_аА»йдг,—— д<?х,=о. |
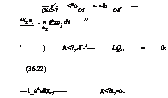 (36.21)
(36.21)
Qio
Диг
Qiq 1 Qm Воспользуемся методом Б. Г. Галеркина, полагая
«ж, - ч44/!1}+А1 вл=й1}/11}+й2)Ж
Д&-,=^(,1)/i2) - f Й9)7f >; AQjc2=ч4Х)у1а)4- (36.23)
Где <?!J) и — собственные функции свободных колебаний шланга (с покоящейся жидкостью) в вертикальной плоскости. Подставив (36.23) в систему уравнений (36.21) — (36.22), после преобразования получим систему уравнений
/y7ci)-|-Јf7(1)+C(1Vr<1)”“C(2Ve<a)==K (36.24)
Л<1)/и)-{-Л<2>7<2>=0. (36.25)
Элементы матриц И, В, С(2 А<-1) и Л(2> и компоненты вектора Ъ даны в приложении 9. Исключая из уравнения (36.24)
Вектор/(2) [используя уравнения (36.21)], окончательно получаем
/ijiu _|_ £?7(1) + С7(1) — ^ (36.26)
Матрицы В и С можно представить в виде
Sin ад (36.27)
C=C(°>-{-C(1)bsin nst -J-C<2> cos /z3?-f C<3> cos 2я3*. (36.28)
Для определения границ главной области параметрического резонанса полагаем
/<1)=Л sin—-t-f-^coS'y-t. (36.29)
Подставив /0) в уравнение (36.26), после преобразований получи м_систему двух уравнений для определения А и В (векторы А и В имеют по две компоненты):
|с<°>—н —i - с<2>+ в<‘> J л + Yj со> — вт 77=0;
(36.30)
I"----- L с<2) -1_ В(0) А + |с<°> - Н С(2) _
Приравняв определитель системы (36.30) нулю, получаем главные области неустойчивости (рис. 36.3) (числовые данные те же, что в предыдущем - примере). “
Области неустойчивости, соответствующие решению с периодом Тг получим, считая
Fm = Ae+A sin/i3T+ficosn3T. (36.31).
После преобразований имеем систему уравнений
С<‘>л, + [с<0> — Нп— уСЮ^Л— Впф 0;
С<*>Яп + В щА + [с<°>- Нп23 + у C<3)J В = 0; (36.32>
С<°«о + ~ С^АЛ(±-С™ -± пф<^В= 0.
 Приравняв определитель системы (36.32) нулю, получим границы областей неустойчивости. Области неустойчивости, соответствующие решению с периодом Т, приведены на рис. 36.4 при а0=0.
Приравняв определитель системы (36.32) нулю, получим границы областей неустойчивости. Области неустойчивости, соответствующие решению с периодом Т, приведены на рис. 36.4 при а0=0.
|
|
Вынужденные параметрические колебания шланга в вертикальной плоскости. Компоненты вектора Ъ для рассматриваемого случая можно преобразовать к виду (приложение 9) с учетом
(36.20)
Bi = bl) sin път-f - b{P cos /г3т+ rf3) sin2 /гчт, (36.33)
Где
MI}= — 2n1'w0w10 J (-хгїсч»!13 + }) de;
М2,= —я, Пз®ю I(І-еЦхІоїГ+лЬїіїі4)*/.; (36.34)
0 ^
Ms>= — ПгЧЯіо (ХШ?11) + Х20'Р2,)) rfe; б
*2*’= — 2п1®0®'10| (х;о¥12>+^,)) й2)= — «і«з®ю f (1 - =) (а:Їо=?І2>+ЛГ20Ї22’) Л;
Ь^6)=—п^іо f (jCio'fS^+Araffz21)^. б
Полагая
/(1>=Л, + Л sin л3т+^ cos я3т, (36.35)
После преобразований получаем систему неоднородных уравнений для определения Л о, А и I?:
С(1)Д,+[С(») - И III —~ C<3>J А - В<°)/г, £= - fc(1); С<2>А0+втп3А f[c(0>~Wn|+-i-C(’)]5=-6(2>. (36.36)
С<°> д, | -І - с<"и (с<2<—й<і)) 27- *о - . - L *(3>.
На рис. 36.5 приведены графики компонент векторов А я В при установившихся параметрических колебаниях в зависимости от безразмерной частоиы ns.