Механика трубопроводов и шлангов

Частные случаи уравнений равновесия трубопровода

Прямолинейный трубопровод. До нагружения внешними си­лами трубопровод имел прямолинейную форму (как, например, па рис. 8.1). В более общем случае внешние силы могут быть направлены и бод любым углом к осевой линин стержня, а де­формации стержня конечными (рис. 8.1). Если сечеиие стержня круглое, то можно считать, что базисы {Г,} и {ёа0} совпадают,! поэтому матрица К есть единичная матрица = а вектор щ тождественно равен нулю.

1. Рассмотрим пространственный случай деформации стерж­ня. Уравнения равновесия сил и моментов совпадают (в проект цпях на неподвижные оси) для внешних сил к моментов, сохра­няющих свое направление, с уравнениями (7.72) — (7.74) и

(7.81) — (7.83). Для следящих сил и моментов следует заменить| в уравнениях (7.72) — (7.74) цХр Рх и в (7.81) — (7.83) ЭДД соответственно на

(8.1)

Для рассматриваемого частного случая уравнения (7.85) и (7.11) — (7.13) преобразуются к виду

	(8.2) (8.3) (8.4)

(8.5)

(8.6)

(8.7)

(8.8)

Уравнения для перемеще­ний принимают следующий •під:

Пня при больших перемЄІЦСИИ-

.14, например, для случая, показанного на рис. 8.1. Считая, что шарнир (правая опора) запрещает перемещения по осям х2 и х$ п і=5*Ю), имеем три условия:

(И( 1)-/2)=0; (ы(1Ы,)=0: <3*,(1)=0-

Если считать, что торцовое сечение не может поворачиваться > шоснтельно шарнирного закрепления (относительно осевой ли­нии), то получаем четвертое условие д(1)=0. В этом случае компоненты момента при є=1 дают еще два условия МХ£ — О {і=2, 3). Шесть условий имеем при є=0. £7(0) =0, 0(0) =0.

Деформации прямолинейного стержия в плоскости чертежа (<“М. рис. 8.1). В этом частном случае (рассматривая деформации

- ІСрЖНЯ В ПЛОСКОСТИ Л^ОЯг) имеем

Х1=х2=Л'1„ = Л^1 = и,=8 = 4’=ул-!=01

Поэтому получаем следующую систему уравнений в проекциях па связанные и неподвижные оси из соотношений (7.1) — (7,13):

—-■^20—|~(Ро+Иі«'?)+їіо+ї,+ У]/)1')8(е-=,)=0;

(8.11)

"^Ч-ХзОю—МА, Ь«,^)+?20+Ї2 (- У] М°8(є + е,)=0; (8.12)

+ «20+!’•:« + Я1ІА (е - г,) = 0; (8.13)

----- **,+/,,-1=0; (/П = С05®); (8-14)

-^-+1'з»і + ;2і=0: (/21= — 5Іп ч>); (8-15)

(8.16)

(8.16)

Система уравнений (8.11) — (8.17) является нелинейной. Если рассматриваются конечные перемещения стержня, то необходима дополнительная информация о поведении внешних сил в про­цессе деформирования стержня.

В связанной системе наиболее просто учитываются следящие силы, т. е. когда известны проекции сил в базисе {ё$}, (Р,{гК </,;0 И у,;о). Следует отметить одну интересную физическую осо­бенность задач статики прямолинейных трубопроводов. В исход­ном состоянии (например, до нагружения силой Р[, рис. 8.1) поток жидкости (если не учитывать силы веса жидкости) не нагружал трубку. При действии силы трубка искривляется и, как следствие этого, появляются распределенные силы, завися­щие от потока жидкости (слагаемое —-—[(/'оН-я^о)^!, кото­рое объединено с осевой силой <3ю(|) и «помогающее» силе Р деформировать стержень).

Уравнения в проекциях на неподвижные оси имеют вид

Криволинейный (в ненагруженном состоянии) трубопровод, осевая линия которого есть плоская кривая. На рис. 8.2 показан участок трубопровода, осевая линия которого лежит в плоско­сти чертежа. Считается, что начальная форма трубопровода из­вестна, т. е. известны изо (к) и ею (є). Возможны два случая: 58
i) внешние С11ЛЫ pw имеют от­личные от нуля проекции на псе три координатные оси, что приводит к пространственной реформации стержня, и б) ииешние силы Р{1) имеют отлич­ные от нуля проекции только на оси, лежащие в плоскости чертежа, что приводит к де­формации стержня в плоскости чертежа. Новое положение осевой линии при действии сил, лежащих в плоскости чер - 1сжа, показано на рис. 8.2 пприхпупктирной линией. По­ручим уравнения равновесия Фубопровода при больших де­формациях для обоих случаев.

1. 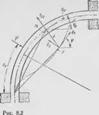Простраисгбенная деформация трубопровода. Уравнения

(7.72) —(7.74) и (7.81) — (7.83) в этом частном случае сохраня­ют форму записи как для общего случая, когда ось стержня в гедеформированиом сосюянии является пространственной кри­вой. Уравнение (7.85), учитывая, что ию=к20—О, принимает вид

(8.26)

Рассмотрим более подробно матрицы преобразования коор - щнат К и Ь. Матрица К связывает векторы базиса {г.,} с векторами базиса {сю}. Для осевой линии стержня, лежащей в плоскости, имеем

Матрица L имеет все элементы отличные от нуля. В более подробной форме записи из уравнения (8.26) имеем (кц — из­вестные функции):

(^11*11+^12*21) - Мл+(*11*12+^12*22) Мхг~~ Хг=А-цУ-1> (8.28)

(/21*11 + ^22*21) + (*21*12 + ^22*22) М А-а + *23^-*« = -^33*2» (8 - 29)

(/»1*11+/32*21) ^.Г1 + (/з1*12+/23*22) МХг + 1шМХз--=Аы{у ,~ **). (8.30)

59

Уравнения для перемещений (7.86) — (7.88) принимают вид

Ди

—~Mi2^2i)=0; (8.31)

Ди „

—^- + ^12 — (^11^12 “h^i2^22)=0; (8.32)

+^13“ ^13—0- (8.33)

2 Плоская (Реформация трубопровода. Рассматривается слу­чай, когда

PjЈ=©4?=ал=о. (8.34)

Следует отмегнть, что для того, чтобы деформация трубопро­вода была плоской, равенство нулю ряда компонент внешних сил и моментов является необходимым, но не достаточным ус - ливием. Чтобы деформация [при выполнении (8.34)] была пло­ской, необходимо, чтобы главная ось инерции сечений трубопро­вода лежала в плоскости чертежа, что всегда выполняется для стержней круглого сечения.

Уравнения равновесия на неподвижные оси в этом случае имеют вил [частный случай уравнений (7.72) — (7.74), (7.81) — 7.83)]

I V,, +fco+ V] Pi?8 (в -0=0; (8.35)

(8.36)

Qx,=CS’ihw^x, {1 = 1, 2);

+ н. х.+ У.®!Й>8(*-*у)=0: (8.37)

Oe. де дв p^j :

(8.38;

Уравнения перемещений при деформации стержня в плоско­сти удобнее представить в виде

Б результате имеем шесть уравнений (8.35) — (8.40) с шестью неизвестными: Qx„ Qv„ А/а, <?, и х2. В уравнениях (8.37),

(8.39) и (8.40) Ху и & — абсолютные координаты точек осевой линии стержня (см. рис. 8.2) Относительные перемещения точек осевой линии стержня при его деформировании определяются из соотношений (см. рис. 5.4)

Јi - — cos <0 — cos <р0, (8.41)

Du*' = — siny-f sin<ft). (8.42)

Oe

Уравнения равновесия в проекциях на связанные оси

- &Л+Y,+ <9,0+ ^ № 0= ■-0=0; (8-43)

|-Q,.a+YA-H»,+ У! 0=0; (8 44)

* *т{

(Qio=eSJl-(^+"i®o), (СЗа=<Йо’);

-^+<320+!%,+ >^(е~О = 0; (8.45)

Де I

Л13=х3 —щ

-^7----- Иа«з+Л1— 1=0 1^и=со®(Ч‘ —40]; (8.46)

<?Е

-^-+»1*3+ <21 = 0 [/21== -ып (<р — ¥о)]- (&ЛТ>

№

Если внешние силы имеют постоянные проекции в неподвиж­ной системе координат («мертвые силы»), то на связанные оси их проекции зависят от перемещений осевой линии стержня, поэтому необходимо их выразить через проекции Рх/7 т. е. вос­пользоваться соотношением

Р<ч=2/*#«!• (8.48)

В рассматриваемом случае деформации стержня в плоскости чертежа матрица характеризующая поворот векторов базиса {/,} относительно векторов базиса {ё? о}, равна