Доклады о будущих и современных технологиях
О РАВНОВЕСИИ ТЯЖЕЛОИ ЧЕТЫРЕХЗВЕННОИ КОНСТРУКЦИИ
М. С. Корнилов, В. Н. Сидоров
Научный руководитель - В. Н. Сидоров, д-р техн. наук, профессор Ярославский государственный технический университет
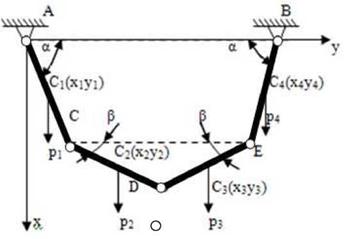 Четыре стержня одной длинны и равного веса соединены друг с другом шарнирами С, Б, и Е. Два крайних стержня вращаются в вертикальной плоскости на шарнирах около неподвижных точек А и В, лежащих на одной горизонтали. Определить зависимость между углами а и в в положении равновесия, если АС=СБ=БЕ=ЕВ=а.
Четыре стержня одной длинны и равного веса соединены друг с другом шарнирами С, Б, и Е. Два крайних стержня вращаются в вертикальной плоскости на шарнирах около неподвижных точек А и В, лежащих на одной горизонтали. Определить зависимость между углами а и в в положении равновесия, если АС=СБ=БЕ=ЕВ=а.
Рассмотрим задачу М. А. Ми - сюрева на равновесие системы стержней АС, СБ, БЕ, ЕВ, равной: Р1 = Р2 = Р3 = Р4 = Р - веса стержней. Воспользуемся принципом виртуальных перемещений:
X (Х5х+У5у+25г) = 0, где Х1 = Х2 = Хз = Х4 = Р; У1 = У2 = = Уз = У4 = 0;
5х1 = (а/2)-ео8(а)5а; 5х2 = = а-ео8(а)5а+(а/2)-ео8(Р)5Р;
5х3 = а-ео8(а)5а+а/2-ео8(Р)5Р; 5х4 = (а/2)-ео8(а)5а;
Соотношения между виртуальными перемещениями будут иметь вид 5р=-(81п(а)/81п(р))5а.
Тогда при равновесии тяжелой четырехзвенной конструкции соотношение между углами а и р tg(а) = 31§(р).