ТЕОРИЯ СИНХРОНИЗАЦИИ МОД В СЛУЧАЕ ОДНОРОДНОГО УШИРЕНИЯ ЛИНИИ
В соответствии с тем, что уже говорилось в разделе 8.6.3, можно построить теорию синхронизации мод лазера при генерации в непрерывном режиме во временном представлении, если потребовать, чтобы форма импульса воспроизводилась после каждого полного обхода резонатора. Ограничимся здесь тем, что обсудим случай однородного уширения линии перехода, при этом будем предполагать, что время жизни на верхнем лазерном уровне много больше времени обхода резонатора. При этих условиях насыщенный коэффициент усиления по мощности за один проход усиливающей активной среды на центральной частоте линии перехода задается выражением g0 = CpN0l, где ар — пиковое значение сечения вынужденного излучения, I — протяженность активной среды, a N0 — инверсия населенностей в стационарном состоянии, установившаяся в результате прохождения многих импульсов. Это означает, что насыщенный коэффициент усиления определяется средней интенсивностью излучения внутри резонатора (/> и, таким образом, может быть выражен через ненасыщенный коэффициент усиления g:
Яо=1+((/>/// (ЕЛ> где Is = hvJapT — интенсивность насыщения усилителя в центре линии перехода.
АКТИВНАЯ СИНХРОНИЗАЦИЯ МОД
Данная теория была разработана Куиценга и Сигманом (D. J. Kuizenga and A. E. Siegman, [1]), а позднее получила развитие в работах Хауса (H. A. Haus, [2, 3]). Далее будем руководствоваться подходом Хауса, и для краткости ограничимся рассмотрением случая синхронизации мод с использованием ампли-
|
^ Зеркало 1 Рис Зеркало 2 Схема резонатора лазера, рассматриваемого при теоретическом анализе синхронизации мод |
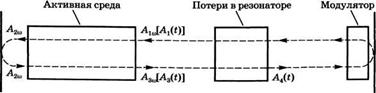
Тудного модулятора. Таким образом, рассмотрим конфигурацию лазера, показанную на рис. Е. 1. Предположим, что модулятор — бесконечно тонкий и находится на минимально возможном расстоянии от зеркала 2. Предполагается, что при указанных условиях импульс излучения распространяется вдоль резонатора туда и обратно (см. рис. 8.19). В любой произвольно выбранной точке внутри резонатора напряженность электрического поля этого импульса можно записать в виде:
E(t) =A(Ј)exp{y'(cы0# - ф)}, (Е.1.1)
Где t — локальное время, позволяющее описать распространение импульса. Тогда спектральная амплитуда Д(со - со0) импульса представляет собой Фурье-об - раз напряженности E(t), т. е.
+00 +00
Д)((о-са0)= j*Ј(0exp (-jat)dt = j*A(f)exp [-Дсо-со0)t]df. (Е.1.2)
-оо —оо
Амплитуда напряженности поля A(t) связана с величиной Аш(со - со0) обратным преобразованием Фурье:
+00
A(t)= - «о )ехр [у(ш - ш0 НМоэ - оз0 ). (Е.1.3)
-оо
|
_ а2ю = *^1со |
![]() Сначала рассмотрим прохождение светового импульса через усилитель. Если А1(й и A2(щ — спектральные амплитуды импульса соответственно до и после одного прохода через усиливающую активную среду (см. рис. Е.1), то можно записать, что A2(ы = tgA1(щ, где te — амплитудный коэффициент пропускания после одного прохода, равный [4]
Сначала рассмотрим прохождение светового импульса через усилитель. Если А1(й и A2(щ — спектральные амплитуды импульса соответственно до и после одного прохода через усиливающую активную среду (см. рис. Е.1), то можно записать, что A2(ы = tgA1(щ, где te — амплитудный коэффициент пропускания после одного прохода, равный [4]
[ехр - цам/с))Х«Ф (Е14)
Здесь п — показатель преломления активной среды, а Асо0 — ширина линии лазерного перехода (FWHM). Заметим, что согласно (Е.1.4) усиление по мощности равно в этом случае:
G(co) = tg2 = ехр^0(со). (Е.1.5)
Коэффициент усиления ^о(со) в этом выражении зависит от частоты следующим образом:
Яо(С0)= {1 + [2((о-со0)/Дюо]2}’ (Е.1.6)
Т. е. имеет лоренцеву форму, как и ожидается в случае однородного уширения линии. Если предположить, что спектральная ширина импульса значительно меньше величины Дсо0, то выражение, стоящее во второй экспоненте в соотношении (Е.1.4), можно разложить в ряд по степеням (со - со0). В первом порядке разложения имеем:
Tg = exp-j{(oml/c) + [g0(a> - ш0)/Дсо0]} x
X exp(g0/2){l - [2(co - со0)/Дсо0]2}. (E.1.7)
Мнимые члены в первой экспоненте соответствуют задержке по фазе ф = = (сonl/c) + [£0(ю - ю0)/Дю0], из которой временная задержка xd, испытываемая импульсом после прохождения через активную среду (см. соотношение (8.6.27)), определяется как gQ
Заметим, что эта задержка не равна п1/с, поскольку усиливающая среда вносит дополнительный вклад в показатель преломления. Величину этой задержки необходимо учитывать при рассмотрении выполнения условия, что время полного обхода импульсом резонатора должно быть равно периоду модуляции потерь. Для простоты в дальнейшем будем пренебрегать этой задержкой, равно как и другими задержками, вызванными остальными элементами резонатора; в любом случае амплитуда импульса относится к локальному времени, в котором эти задержки уже учтены. Поэтому пренебрежем фазовым членом в выражении (Е. 1.7) и запишем
|
(Е.1.9) |
![]() Tg = exp{(g0/2){l - [2(со - со0)/Дсо0]2}}.
Tg = exp{(g0/2){l - [2(со - со0)/Дсо0]2}}.
Не будем также учитывать тот факт, что коэффициент отражения зеркала 1 имеет конечное значение, так как это обстоятельство будет учтено в общих потерях резонатора. После второго прохода через активную среду спектральную амплитуду импульса нужно вновь умножить на коэффициент пропускания tg, заданный выражением (Е.1.9). Таким образом, коэффициент пропускания после полного прохода через усилитель будет равен
= (Аза MiJ = exp {(£о){1 - [2(со - со0)/Ао)о]2}}.
Где А3а — спектральная амплитуда импульса после одного полного прохода. Предполагая, что g0 1, из последнего уравнения получаем:
А3ю =t§Ala = А1ю(1 + (£о){1-[2(со - «0)/А(й0]2}). (Е.1.10)
При дальнейшем рассмотрении необходимо рассчитывать влияние такого пропускания во временном, а не в частотном представлении. В связи с этим вспомним следующее свойство преобразования Фурье (FT):
|
DnA(t) Dtn |
![]()
|
FT |
![]() = [7'(ю-соо)]пА>(ш-соо).
= [7'(ю-соо)]пА>(ш-соо).
Это соотношение нетрудно доказать, взяв сначала производную л-ого порядка, а затем осуществив преобразование Фурье для обеих частей выражения (Е. 1.3). Соотношение (Е.1.11) показывает, что умножение спектральной амплитуды Аа на к(со - со0)п, где к — постоянная, во временном представлении равнозначно умножению производной п-ото порядка от амплитуды А(£) на (к/]п). Применяя это свойство к каждому слагаемому в правой части уравнения (Е. 1.10), получим:
|
Аг(і), |
|
1 + |
|
Лсоо ) dt2 |
|
A%(t) -4l + g0 |
|
|
Где А^) и А3(£) — соответственно амплитуды импульса до и после полного прохода через усилитель (см. рис. Е.1). Из соотношения (Е.1.12) легко видеть, что результат прохода импульса через усиливающую среду можно описать оператором
Полного прохода:
|
1 + £о |
![]()
|
Dt2 |
![]() (Е.1.13)
(Е.1.13)
Теперь учтем влияние постоянных потерь в резонаторе, связанных с конечными коэффициентами отражения зеркал и с внутренними потерями. Эти потери схематически представлены на рис. Е.1 в виде прямоугольника в центре. Запишем амплитуду импульса после одного прохода через резонатор в виде:
А4а) = [ехр(-у/2 )]А3(1), (Е.1.14)
Где у — логарифмические потери мощности за одни проход. Отношение интенсивностей (/4//3) = (А4/А3)2, согласно соотношению (Е.1.14), равно, как и ожидалось, величине ехр (-у). Из (Е.1.14) получаем, что пропускание, соответствующее потерям за полный обход резонатора, составляет ехр (-у), что, при у <С 1, приближенно равно 1 - у. Это значит, что оператор, соответствующий потерям за полный проход в резонаторе, имеет простой вид:
2}= 1-у. (Е.1.15)
В заключение рассмотрим действие амплитудного модулятора. Пусть ут[1 -
- cos (comf)] — логарифмические потери мощности за один проход. В этом выражении сош — частота модулятора. Она предполагается такой, что период модуляции равен времени полного обхода резонатора импульсом. Тогда амплитудный коэффициент пропускания модулятора при одном проходе равен:
= exp{-(ym/2)[l - cos((Bm*)]}.
(Е.1.16)
Пропускание за двойной проход через модулятор составит
4= ехр {-(ут)[1-С08 (С0т*)]},
Что при ут С 1 приближенно равно = 1-(ут)[1-со8(сот£)]. Теперь допустим, что
Импульс проходит через модулятор тогда, когда потери модулятора равны нулю (см. рис. 8.20), т. е. в момент времени £ = 0. Предположим также, что длительность импульса много меньше периода модуляции 2п/(от. При этих допущениях пропускание за полный проход можно аппроксимировать выражением =1-(ут/2)(сот£)2- Тогда оператор, соответствующий двойному проходу импульса через модулятор, задается простым выражением:
(Е.1.17)
Определив операторы, описывающие эволюцию импульса во времени при двойном проходе через три рассматриваемых элемента резонатора, потребуем, чтобы в стационарном состоянии амплитуда импульса воспроизводилась после полного обхода резонатора. Запишем:
ТтТ, ТеА(П = АУ). (Е.1.18)
Используя выражения, полученные выше для Тт,7}и7^, а затем учитывая условия [#0, у, ут]< 1, получаем следующее дифференциальное уравнение:
|
1 + |
|
Асо0 ) dt2 |
|
-у-If a2mt* ^A(t) = 0, |
|
|
|
(Е.1.20) |
![]() Которое является окончательным результатом вычислений. Легко видеть, что это уравнение по форме аналогично уравнению Шредингера для частицы в параболической потенциальной яме (гармоническому осциллятору), решения которого хорошо известны. В рассматриваемом случае можно записать:
Которое является окончательным результатом вычислений. Легко видеть, что это уравнение по форме аналогично уравнению Шредингера для частицы в параболической потенциальной яме (гармоническому осциллятору), решения которого хорошо известны. В рассматриваемом случае можно записать:
A(t) = Hn(apt)ex р где Нп — эрмитов полином л-го порядка, а
|
Ут " |
1/4 |
0 3 < S 3 |
|
_2g0_ |
2 |
|
1/2 |
Причем величина £0 такова, что
1-^ = М(2п + 1). (Е.1.22)
Однако можно показать, что из всех этих решений устойчивым является лишь гауссово решение первого порядка (п = 0).
Выражения (Е.1.21) и (Е.1.22) можно рассматривать как два уравнения с двумя неизвестными параметрами (ор и #0. Зная сор, можно найти длительность импульса, полученного в результате синхронизации мод. Полная ширина на половине высоты (Е¥НМ) для импульса интенсивности Атр фактически задается выражением Атр = 2[1п2]1/2/сор. Таким образом, из соотношения (Е.1.21) получаем:
|
«аУ (_1_у 1т) Ут ДУ0^ |
![]()
|
2ч/21п2 |
![]() Л1/4/ Л1/2
Л1/4/ Л1/2
(Е.1.23)
Лтр =
Где т = сош/2я и Ау0 = Аю0/2я. Отметим, что первый сомножитель в правой части выражения (Е.1.23) приблизительно равен 0,45; тогда как второй сомножитель, вследствие возведения в степень 1/4, приблизительно равен единице. Величины Дтр и, следовательно, сор слабо зависят от #0. Пользуясь соотношением (Е. 1.23), получаем следующее приближенное выражение для Атр (см. (8.6.19)): Дтр = 0,45/ (ушДу0)1/2. Из (Е.1.22) находим значение^, полагая п = 0. Заметим, что, в соответствии с соотношением (Е.1.22), оказывается больше у вследствие наличия потерь в модуляторе. Если величина^ найдена, то из соотношения (Е.1) можно определить среднюю интенсивность излучения <I) внутри резонатора, так как ё = = ху, где х = Л7ЛГС = Кр/Крс — величина, при которой происходит превы
Шение порога. По известным средней интенсивности излучения внутри резонатора, длительности и частоте следования импульсов можно найти пиковую интенсивность лазерного импульса.