ПРИНЦИПЫ ЛАЗЕРОВ

УПРОЩЕННОЕ ОПИСАНИЕ УСИЛЕННОГО СПОНТАННОГО ИЗЛУЧЕНИЯ

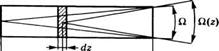
Предположим, что усиленное спонтанное излучение (УСИ) распространяется в активной среде в обоих направлениях и, таким образом, будем рассматривать ее конфигурацию, показанную на рис. В. 1. Допустим также, что усиливающая среда ведет себя как идеальная четырехуровневая система, населенностью нижнего уров­ня в которой можно пренебречь. Далее рассмотрим переходы как с однородно-, так и с неоднородно-уширенным контуром линии. Подробное теоретическое рассмот­рение характеристик УСИ при данных условиях было выполнено Касперсоном [1]. Однако эта теория достаточно сложна, и вследствие этого нельзя непосредственно проследить основные физические особенности УСИ. Следуя одной из последних работ [2], представим здесь упрощенное описание УСИ, целью которого является получение некоторых асимптотических выражений, позволяющих охарактеризо­вать спектральный контур линии УСИ в режиме слабого насыщения.

Предположим, что в режиме слабого насыщения населенность верхнего уров­ня Ы2 и, следовательно, инверсия населенностей N = ЛГ2 не испытывают заметного изменения за счет интенсивности УСИ. Пусть /у(г, V) — спектральная интенсив­ность распространяющегося вдоль положительного направления оси г пучка УСИ в точке г (см. рис. В. 1). В элементарном изменении интенсивности (И„ вдоль оси г следует учитывать вклад не только от вынужденного, но и от спонтанного излуче­ния в тонком слое толщиной <1г. Таким образом, можно записать:

(В.1)

Где ау — сечение вынужденного излучательного перехода на частоте V, Д, — веро­ятность спонтанного излучательного перехода на той же частоте, а 0(2:) — телес­ный угол, под которым виден выходной торец активного элемента из центра слоя йг. Отметим, что множитель 0(г)/4я, стоящий в правой части (В.1), отража­ет тот факт, что спонтанное излучение из слоя йг распространяется равномерно в телесном угле 4л, тогда как в данном случае представляет интерес только та его часть, которая испускается в телесный угол 0(2).

Вычисление спектральной интенсивности УСИ, распространяющегося вдоль оси г

Для того чтобы вычислить спектральную интенсивность У СИ JV(J, v) на выхо­де из активной среды, т. е. при 2 = 1, необходимо проинтегрировать уравнение - (В.1) по координате г. Учитывая, что основной вклад в УСИ дают области актив­ной среды, расположенные вблизи 2 = 0, излучение из которых испытывает наи­большее усиление, МОЖНО ПОЛОЖИТЬ 0(2) = Q, где Q — телесный угол, под которым виден один торец активного элемента из центра другого торца (см. рис. В.1). То­гда уравнение (В.1) можно легко проинтегрировать и, с учетом граничного усло­вия Jv(0, v) = 0, получить:

<в-2>

Учитывая, что Д, = Ag(v - v0) и av = a^(v - v0)/gp9 где А — вероятность спон­танного излучения, g(v - v0) — функция, описывающая спектральную форму кон­тура линии перехода, с пиковым значением gp, — пиковое значение сечения, а

V0 — центральная частота перехода, соотношение (В.2) можно переписать в виде:

Jv(Z, v) = ф/^Дехр (avNl) -1], (В. З)

Где ф = т/тг = тА — квантовый выход люминесценции (см. (2.6.22)), а I8 = hv/opт — интенсивность насыщения усиливающей среды на частоте перехода (см. (2.8.24)).

Интенсивность УСИ на произвольной частоте v, нормированную на макси­мальное значение, можно легко получить из соотношения (В. З): [/V(J, v)//v(i, v0)] = = [exp (o^Nl) - l]/[exp(<JpNl) - 1]. Как для лоренцевой, так и для гауссовой линий спонтанного излучения нетрудно рассчитать форму спектра УСИ при заданном значении пикового логарифмического коэффициента усиления за один проход G = exp (OpNl). Например, на рис. 2.24 сплошными кривыми показаны спектраль­ные контуры УСИ в зависимости от нормированного частотного сдвига 2(v - v0)/ Av0, рассчитанные для лоренцевых линий излучения при значениях пикового усиления, равных 103 и 106. С другой стороны, приближенное выражение для ширины линии УСИ Av^ можно получить из (В. З), допустив, что форма контура линии УСИ с достаточной точностью описывается гауссовой функцией. Тогда можно записать:

TOC o "1-5" h z [exp (oxNl) - 1] = [exp (GpNl) - 1] х exp (-kx2), (B.4)

Где k — константа, ax — нормированный сдвиг частоты

X = 2(v-v0)/Av0, (В.5)

В котором Av0 — ширина линии перехода (как при однородном, так и при неодно­родном уширении перехода). Из (В.4) легко получить выражение для kx2:

Kx2 = In [exp (GpNl) - 1] - In [exp (оДО - 1]. (B.6)

Обозначив функцию в правой части уравнения (В.6) через f(x), находим кон­станту k из соотношения:

Ач

<в-7>

Рассматривая случай лоренцевой линии, подставляем в (В.6) выражение стх = ар/(1 + х2). После продолжительных, но несложных преобразований получа - ей нз (Б.7); . _С1пС

(С-1>- (В-8)

Аналогично в случае гауссовой линии подставляем стх = <трехр -(д:21п 2) в (В.6) и из (В. 7) получаем, что

( )(С-1). (в-9)

В рамках сделанного выше предположения о гауссовой форме контура У СИ его полная нормированная ширина, выраженная в единицах нормированного сдвига частоты х, дается соотношением Ах^ = 2(1п 2/&)1/2. Поскольку, согласно - (В.5), = Ах^ х (Ду0/2), то ширину контура линии УСИ можно найти из пре­

Дыдущего выражения, если значение Ч задано соотношениями (В.8) или (В.9). Таким образом, получаем, что

Луа8£=[1п2]1/2[^]1/2Ду0 <ВЛ°)

Для лоренцевой и

Г С-1 ~11/2

Ау° (В-11)

Для гауссовой линий спонтанного излучения. Выражение (В. 10) было использо­вано, например, для получения зависимости нормированной ширины линии УСИ АА8Е/А[о от величины параметра = 1п О, которая графически изображена пунктиром на рис. 2.25.

С помощью проведенного описания формы спектрального контура УСИ мож­но найти приблизительное выражение для полной интенсивности УСИ I =

На выходе из активной среды. Для этого проинтегрируем левую и правую части соотношения (В. З) по частоте V и получим:

+00

1=Ф/*(ёК 1[ехр (а'т) ~1]сгу* (В-12>

—00

Исходя из предположения о гауссовой форме контура спектра УСИ, задавае­мой приближенным выражением (В.4), и учитывая соотношение (В.8) или (В.9), интеграл в соотношении (В. 12) вычислить нетрудно. Имеем (см. (2.9.3)):

_Q_WG-1)3^

4rc3/2j[GlnG]1/2 (Bld)

Для лоренцевой и,

Р Q (G-l)3/2

I4^/[GlnG]1/2 (В.14)

Для гауссовой линий спонтанного излучения.

ЛИТЕРАТУРА

1. L. W. Casperson, Threshold Characteristics of Mirrorless Lasers, J. Appl. Phys. 48, 256(1977).

2. O. Svelto, S. Taccheo and C. Svelto, Analysis of Amplified Spontaneous Emission: Some Corrections to the Lyndford Formuls, Opt. Commun. 149, 277 (1988).