РАСЧЕТ ФОРМЫ ЛИНИИ ПРИ СТОЛКНОВИТЕ ЛЬНОМ УШИРЕНИИ
Как показано в разделе 2.5.1, форма линии при столкновительном ушире - нии может быть получена из нормированной спектральной плотности - ) волны синусоидальной формы, испытывающей случайные скачки фазы (см. рис. 2.9). Напряженность электрического поля электромагнитной волны, изменяющаяся во времени так, как представлено на рис. 2.9, может быть описана следующим образом:
|
(Б.1) |
![]() Е(г) = £0ехр Дсо* - ф(0]>
Е(г) = £0ехр Дсо* - ф(0]>
|
—00 |
![]() Где Е0 — вещественная постоянная, со = 2яу — угловая частота излучения, а фаза ф(£) испытывает случайные скачки при каждом столкновении атомов. Будем предполагать, что плотность вероятности рх(т) распределения интервалов времени т между двумя последовательными столкновениями описывается выражением (2.5.7). Удобнее всего проводить расчет функции §(у' - V) в шкале угловых частот со, т. е. определять функцию g((o, - со). Очевидно, что - )й' = £(со' - со)с£со', откуда g{V - ч) = 2я£(со' - со). Функция £(со' - со) с точностью до коэффициента пропорциональности определяется спектральной плотностью мощности Щсо' - со) электромагнитной волны, изображенной на рис. 2.9. Для того чтобы этот коэффициент равнялся единице, потребуем, согласно (2.5.4), чтобы для Щсо' - со) выполнялось соотношение |Щсо' - со)(2со' = 1. Следует заметить, что в соответствии с теоремой Парсеваля
Где Е0 — вещественная постоянная, со = 2яу — угловая частота излучения, а фаза ф(£) испытывает случайные скачки при каждом столкновении атомов. Будем предполагать, что плотность вероятности рх(т) распределения интервалов времени т между двумя последовательными столкновениями описывается выражением (2.5.7). Удобнее всего проводить расчет функции §(у' - V) в шкале угловых частот со, т. е. определять функцию g((o, - со). Очевидно, что - )й' = £(со' - со)с£со', откуда g{V - ч) = 2я£(со' - со). Функция £(со' - со) с точностью до коэффициента пропорциональности определяется спектральной плотностью мощности Щсо' - со) электромагнитной волны, изображенной на рис. 2.9. Для того чтобы этот коэффициент равнялся единице, потребуем, согласно (2.5.4), чтобы для Щсо' - со) выполнялось соотношение |Щсо' - со)(2со' = 1. Следует заметить, что в соответствии с теоремой Парсеваля
(Б.2)
|
(Б. З) |
![]() Условие М^со' - со)с/со' = 1 требует, таким образом, выполнения равенства 2пе$ =1. Следовательно, функция #(со' - со) соответствует спектральной плотности мощности сигнала Е{Ь), заданного выражением (Б.1) и имеющего амплитуду
Условие М^со' - со)с/со' = 1 требует, таким образом, выполнения равенства 2пе$ =1. Следовательно, функция #(со' - со) соответствует спектральной плотности мощности сигнала Е{Ь), заданного выражением (Б.1) и имеющего амплитуду
Е0 = (2я)~1/2.
|
+00 |
![]() Для расчета спектральной плотности мощности - со) сигнала, заданного выражением (Б.1), воспользуемся теоремой Винера-Хинчина, согласно которой
Для расчета спектральной плотности мощности - со) сигнала, заданного выражением (Б.1), воспользуемся теоремой Винера-Хинчина, согласно которой
- со) можно получить как Фурье-образ автокорреляционной функции сигнала Г(т). Таким образом, можно записать
Где автокорреляционная функция Г(т) имеет вид:
+т
Г(т) = lim і + Т)dt.
-т
Для волны, изображенной на рис. 2.9, запишем:
|
Г(т)=Шп^Е^ехр (/ют) |
![]()
|
(Б.6) |
![]() Г(т)=Ит^Е^ехр (/ют)| | dt+ J exp [-ДДф)]^
Г(т)=Ит^Е^ехр (/ют)| | dt+ J exp [-ДДф)]^
Xorr. ипсогг.
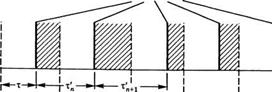
Первый интеграл в правой части (Б.6) вычисляется на временных интервалах между —Т и +Tj в течение которых не происходит столкновений, вызывающих скачки фазы, и, таким образом, сигналы E(t) и E(t + т) имеют одинаковые фазы (коррелированные интервалы). Второй интеграл в правой части (Б.6) вычисляется на временных интервалах, в течение которых происходит столкновение, и поэтому сигналы E(t) и E(t + т) имеют случайную разность фаз Аф (некоррелированные интервалы). Эту ситуацию можно схематически изобразить так, как это сделано на рис. Б. 1, где сплошные вертикальные линии показывают моменты времени, в которые происходят скачки фазы сигналов E(t) и E(t + т). Проецируя вертикальные линии графика E(t + т) на график E(t) (вертикальные пунктирные линии), получаем коррелированные временные интервалы, изображенные заштрихованными участками.
![]() Найдем Г(т) из выражения (Б.6). Прежде всего заметим, что вклад второго интеграла в правой части (Б.6) стремится к нулю при больших Т9 так как подынтегральное выражение ехр-у(Аф) — случайное число, среднее значение которого равно нулю. Таким образом, уравнение (Б.6) принимает вид:
Найдем Г(т) из выражения (Б.6). Прежде всего заметим, что вклад второго интеграла в правой части (Б.6) стремится к нулю при больших Т9 так как подынтегральное выражение ехр-у(Аф) — случайное число, среднее значение которого равно нулю. Таким образом, уравнение (Б.6) принимает вид:
(Б. 7)
Интеграл в (Б. 7) равен полному времени корреляции фаз, т. е. сумме длительностей промежутков времени, соответствующих заштрихованным участкам на рис. Б. 1. Если т'п — длительность временного интервала между п-м и (п + 1)-м скачками фазы (см. рис. Б.1), то полное время корреляции фаз можно записать как
|
|
|
|
|
Скачки фазы функций |
|
E(t) |
|
> T |
Рис. Б.1
Скачки фазы функций
E(t) и E(t + х):
|
Скачки фазы функций |
![]() Заштрихованные области со-
Заштрихованные области со-
Ответствуют временным ин-
T тервалам, в которых функции коррелируют.
Где суммирование производится по т'л, для которых справедливо соотношение т'п > т. Таким образом, уравнение (Б. 7) можно представить в виде:
Г(т) = £^ехр (уют)Цт^Ц^ —. (Б.8)
Обозначим число скачков фазы между - Т и +Т буквой ЛГ, тогда
Где тс = 2 Т/Ы — длительность среднего интервала времени между двумя последовательными скачками фазы, а ((т' - т)) — среднее значение (т' - т) (при условии т' > т). Используя выражение (2.5.7) для плотности вероятности распределения длительности временного интервала между последовательными скачками фазы, находим для ((т' - т)):
+00
|
(Б. 10) |
![]() <т'-т>=(1/тс) |(т'-т)ехр Нт'/хс)]</т' = тсехр [-(х/хс)].
<т'-т>=(1/тс) |(т'-т)ехр Нт'/хс)]</т' = тсехр [-(х/хс)].
Из (Б.8), (Б.9) и (Б. 10) получаем выражение для корреляционной функции: Г(т) = Е§ехр [уют - (т/тс)]. Если функция Г(т) задана также для значений т < 0, то, поскольку должно выполняться соотношение Г(-т) = Р(т), окончательный результат будет иметь вид:
Г(т) = £|ехр [усох —([ т | /тс)3. (Бл1)
Используя теорему Винера-Хинчина (см. (Б.4)), вычислим спектральную плотность мощности Т^(со' - со), а из нее, подставляя выражение (Б. З) для сигнала Е09 найдем #(со' - со). Получаем:
(Б12)
Ввиду того, что g(V - V) = 2я#(со' - со), можно записать последний результат в виде (см. (2.5.9)):
8(У' ~ У) = 2Тс [1 + (V - - у)24яЧ2]’ (Б-13)
Откуда нетрудно получить форму линии, которая определяется соотношением (2.5.10).