ПАРАМЕТРИЧЕСКАЯ ГЕНЕРАЦИЯ
Перейдем теперь к обсуждению процесса параметрической генерации. Следует вначале заметить, что идеи, высказывавшиеся ранее в связи с ГВГ, нетрудно распространить и на случай двух падающих волн с частотами сох и со2, суммирующихся в волну с частотой ©3 = 0)! + со2 (генерация суммарной частоты). Генерацию гармоник можно в действительности представить как предельный случай генерации суммарной частоты, когда сог = со2 и Щ = 2со. Физическая картина опять напоминает случай ГВГ — благодаря наличию нелинейного соотношения (12.4.2) для величины PNL и полного поля Е [Е = Ещ (z, t) + Е^2 (2, t)], между волной с частотой о*! и волной с со2 возникают биения, что приводит к образованию компоненты поляризации с частотой (03 = «1 + (02. Это, в свою очередь, приводит к излучению электромагнитной волны с частотой со3. Таким образом, в случае генерации суммарной частоты можно записать следующее равенство:
+ fm2 = heо3, (12.4.18а)
Которое (в представлении фотонов, а не полей) означает, что в данном процессе исчезают один фотон с частотой и один фотон с частотой со2, в то
Время как образуется фотон с частотой со3. Таким образом, можно предполо
Жить, что в этом случае импульс фотонов также сохранится, т. е.
Нкг + Нк2 = Як3. (12.4.186)
Это соотношение записано в общей форме, причем величина к является вектором. Соотношение (12.4.186), которое выражает условие фазового синхронизма в случае генерации суммарной частоты, можно рассматривать как прямое обобщение этого условия для ГВГ (ср. с соотношением (12.4.126)).
Оптическая параметрическая генерация в действительности представляет собой процесс, обратный генерации суммарной частоты. В этом случае волна с частотой со3 (частота накачки) генерирует две волны (называемые «холостой» и «сигнальной» волнами) с частотами и со2 таким образом, что полные энергия и импульс фотона сохраняются, т. е.
Heо3 = hcot + hiо2, (12.4.19а)
Hks = hk1 + hk2. (12.4.196)
Физическую картину процесса, имеющего место в этом случае, можно попытаться описать следующим образом. Представим сначала, что в нелинейном кристалле присутствуют одновременно сильная волна с частотой со3 и слабая волна с частотой о^. В результате нелинейного взаимодействия (см. соотношение (12.4.2)) волна с частотой со3 образует биения с волной, имеющей частоту сох, что приводит к возникновению компоненты поляризации с частотой со3 - coj = со2. Если при этом удовлетворяется условие фазового синхронизма (12.4.196), то волна с частотой со2 будет нарастать по мере своего прохождения через кристалл. В этом случае полное поле Е будет в действительности суммой трех полей [Е = Есо^г, t) + Е<о2(г, t) + 2£со3(г, £)],а между волнами с частотами со2 и со3 будут возникать биения, что приведет к появлению
|
|
|
|
|
|
|
|
|
|
|
|
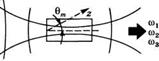
Компоненты поляризации с частотой со3 - со2 = щ. Эта поляризация также вызовет нарастание волны с частотой <о1в Следовательно, от волны с частотой со3 энергия будет передаваться волнам с частотами и со2, и исходная слабая волна с частотой (ог будет усилена. Из этой картины видно, в чем состоит коренное отличие параметрической генерации от ГВГ. Если в последнем случае для осуществления процесса ГВГ необходимо иметь лишь один сильный пучок на основной частоте, то в первом случае необходимо иметь также и слабый пучок волны с частотой щ, причем система ведет себя как усилитель для волны % (и со2). Однако на практике нет необходимости вводить слабый сигнал от внешнего источника (например, от другого лазера), поскольку он генерируется внутри кристалла в виде шума (называемого параметрическим шумом). Из этого шума можно затем генерировать когерентные пучки аналогично тому, как это делается в лазере. С этой целью в оптический резонатор помещается нелинейный кристалл, который накачивается сфокусированным пучком накачки (рис. 12.8). В таком параметрическом генераторе оба зеркала (1 и 2) имеют высокий коэффициент отражения (например, R = 1 и R2 = 1) либо только на частоте щ (однорезонансный генератор), либо на двух частотах coj и со2 (двухрезонансный генератор). Для пучка накачки зеркала являются достаточно прозрачными. Генерация возникает, когда усиление, обусловленное параметрическим эффектом, начнет превышать потери в оптическом резонаторе. Следовательно, для начала генерации необходима некоторая пороговая энергия входного пучка накачки. Когда этот порог достигнут, генерация наступает как на частоте щ, так и на частоте со2, а конкретное сочетание величин и сэ2 определяется соотношениями (12.4.19). Например, при условии фазового синхронизма типа1, в котором участвуют необыкновенная волна с частотой со3 и обыкновенные волны с частотами а>! и сэ2 (т* е* е(оЗ °coi + °ю2)> из соотношения (12.4.196) получаем:
|
(12.4.20) |
![]() С03пе((0з, со) = Ю^оСсЙ!) + С02По((02).
С03пе((0з, со) = Ю^оСсЙ!) + С02По((02).
При заданном значении угла 0 (т. е. при известном наклоне нелинейного кристалла по отношению к оси резонатора) выражение (12.4.20) определяет связь между со! и со2, а вместе с соотношением (12.4.19а) оно позволяет вычислить обе частоты со! и со2. Можно реализовать условия фазового синхронизма как типа I, так и типа II (например, ею3 —» ою1 + еа2 в отрицательном одноосном кристалле), а перестройку можно осуществлять изменением либо наклона кристалла (угловая перестройка), либо температуры (температурная перестройка). В заключение заметим, что если усиление, обусловленное параметрическим эффектом, достаточно велико, то можно обойтись без зеркал, а интенсивное излучение на частотах сох и со2, происходящее от параметрического
шума, можно получить за один проход через кристалл. Такое поведение часто называют суперлюминесцентным параметрическим излучением, а соответствующее устройство — оптическим параметрическим генератором (ОПГ).
На практике применяются как однорезонансные, так и двухрезонансные оптические параметрические генераторы. Двухрезонансную параметрическую генерацию можно получить при накачке как непрерывными, так и импульсными лазерами. Как оказалось, в случае непрерывной накачки пороговые мощности составляют всего несколько милливатт. Однако следует заметить, что наличие резонанса сразу на двух частотах вызывает некоторую нестабильность выходного излучения как по амплитуде, так и по частоте. Однорезонансная параметрическая генерация вначале была осуществлена лишь при накачке импульсными лазерами, поскольку в случае резонанса на одной частоте пороговая мощность накачки оказывается значительно более высокой (на два порядка величины), чем в случае двухчастотного резонанса. Тем не менее, с развитием более совершенных нелинейных кристаллов стала осуществима и непрерывная однорезонансная генерация. Кроме того, в однорезонансных генераторах стабильность сигнала на выходе оказывается намного выше, и по этой причине наиболее распространенными являются именно такие устройства. Оптические параметрические генераторы позволяют получать когерентное излучение в диапазоне длин волн от видимого до ближнего ИК (0,5-5 мкм). Наиболее успешными конструкциями являются те, в которых используются кристаллы ВВО, ЬВО и ниобата лития (1лМЬ03). ОПГ могут также генерировать когерентное излучение и на более длинных волнах ИК-диапазона (примерно до 14 мкм), если использовать в них такие кристаллы, как селенид серебра-галия (А£Оа8е2) и селенид кадмия (Сс18е). Синхронная накачка оптических параметрических генераторов, включая накачку в режиме синхронизации мод, оказывается весьма перспективной в плане генерации коротких импульсов когерентного излучения с перестройкой частоты в очень широком диапазоне. Характерная особенность таких устройств заключается в том, что их усиление определяется пиковой мощностью импульса накачки, а это означает, что для достижения необходимого порога достаточно небольших средних мощностей (нескольких милливатт), даже для случая однорезонансной схемы. В заключение следует отметить, что на практике КПД оптических параметрических генераторов может быть очень высоким, приближаясь к теоретическому значению эффективности преобразования (100%).