ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ
Рассмотрим монохроматическую плоскую волну с частотой ю, распространяющуюся в направлении z через нелинейный кристалл. При этом полагается, что начало оси z совпадает с входным торцом кристалла. Для электрического поля EJ(z, t) плоской электромагнитной волны постоянной интенсивности можно записать следующее выражение:
Жco(z> t) = (1/2){E(z, ю)ехр [y(cof - ktвz) + с. с.}. (12.4.3)
В этом выражении «с. с.» обозначает величину, комплексно-сопряжен - ную первому члену суммы в фигурных скобках, а
= (12.4.4)
С
Где — скорость света в кристалле, па — показатель преломления на частоте со и с — скорость света в вакууме. Подставляя выражение (12.4.3) в (12.4.2), можно показать, что величина PNL содержит член[76], соответствующий генерации на частоте 2со, а именно:
PZL =(s0d/2){Ј2(z, fф)exp [j(2(щt-2fcwz)] + c. c.}. (12.4.5)
Это выражение описывает поляризацию, осциллирующую на частоте 2© и распространяющуюся в пространстве в виде волны с волновым числом 2к&. Данная волна поляризации излучает на частоте 2ю, что подразумевает генерацию электромагнитной волны на частоте второй гармоники 2ю. Аналитическое рассмотрение, приводимое ниже, включает в себя подстановку данного значения поляризации в волновое уравнение электромагнитного поля. Электрическое поле этой электромагнитной волны запишется в виде:
Е2е>(2, г) = (1/2){-Е(2, 2(о)ехр [Д2(о£ - к2аг)] + с. с.}, (12.4.6)
|
Где |
![]() , 2(0 2п2шсо
, 2(0 2п2шсо
|
(12.4.7) |
![]() ^2 со
^2 со
Определяет волновое число на частоте 2ю. Таким образом, обращаясь снова к нелинейному соотношению (12.4.2), физический смысл ГВГ можно понять как результат биений электромагнитной волны на основной частоте ю с самой собой, что приводит к поляризации, осциллирующей с частотой 2©., Сравнивая выражения (12.4.5) и (12.4.6), можно получить очень важное условие, которое должно выполняться, чтобы процесс ГВГ протекал эффективно. Другими словами, фазовая скорость волны поляризации (иР = 2ю/ 2ка) должна быть равна фазовой скорости генерируемой электромагнитной волны (иЕ = 2ю/&2со). Это условие можно записать в виде:
(12.4.8)
Действительно, если это условие не удовлетворяется, то на некотором расстоянии I (т. е. при г = I) внутри кристалла фаза волны поляризации (т. е. фаза 2к^1) будет отличаться от фазы (к2^1) генерируемой волны, которая пришла от точки 2 = 0в точку г = I. Эта увеличивающаяся с расстоянием I разность фаз (2к& - к2а)1 означает, что генерируемая волна не будет кумулятивно расти с расстоянием /, поскольку она не поддерживается поляризацией с соответствующей фазой. Поэтому условие (12.4.8) называется условием фазового синхронизма. Заметим, что в соответствии с (12.4.4) и (12.4.7) это условие можно записать в виде:
|
^2со Па- |
![]() (12.4.9)
(12.4.9)
Теперь, если бы направления векторов и Рмь (а следовательно, и Е2т) действительно совпадали (что подразумевается в (12.4.2)), то условие (12.4.9) не выполнялось бы из-за дисперсии кристалла (Ап = п2сй - п^). Это накладывает жесткое ограничение на длину кристалла 1СУ на протяжении которой величина Рмь все еще может дать кумулятивно складывающиеся вклады и тем самым создать волну второй гармоники. Длина 1С (длина когерентности) должна соответствовать расстоянию, на котором фаза волны поляризации и фаза волны второй гармоники отличаются друг от друга на число я, т. е. к2ш1с - 2кы1с = я. Используя выражения (12.4.4) и (12.4.7), это условие можно записать в виде:
|
|
(12.4.10)
Где X = 2пс/со — длина основной волны в вакууме. Выбрав, например, А, = 1 мкм и Ап~ 10~2, получим 1С = 25 мкм. Следует заметить, что на таком расстоянии в кристалле волна поляризации отличается по фазе от волны второй гармоники на 180° и, таким образом, волна второй гармоники, вместо того чтобы продолжать нарастать, начинает затухать. В этом случае, когда величина 1С столь мала, лишь очень небольшая часть падающего излучения может быть преобразована в волну второй гармоники.
На этой стадии рассуждений имеет смысл указать на другой полезный способ описания процесса ГВГ, а именно через фотоны, а не через поля. Для начала запишем соотношение между частотой основной волны (со) и волны второй гармоники (со5Я):
|
— 2со. |
![]() (12.4.11)
(12.4.11)
Если теперь умножить обе части соотношений (12.4.11) и (12.4.8) на константу Й, то получим:
|
|
||
Соответственно. Для того чтобы в процессе ГВГ энергия сохранялась, должно выполняться равенство (II2где 12© и Ло — интенсивности соответствующих волн. С помощью выражения (12.4.12а) получаем йР2(й/(12 = = -(1 /2)й¥а)/йг, где 2^2© и — потоки фотонов этих двух волн. Из этого последнего равенства можно заключить, что в процессе ГВГ, когда исчезают два фотона с частотой со, вместо них появляется один фотон с частотой 2со. Таким образом, соотношение (12.4.12а) можно рассматривать как закон сохранения энергии фотонов. Если вспомнить, что импульс фотона равен Нк, то соотношение (12.4.126) есть не что иное, как условие того, что в процессе ГВГ должен сохраняться и импульс фотонов.
Рассмотрим теперь снова условие фазового синхронизма (12.4.9) и покажем, когда оно должно выполняться в соответствующем оптически анизотропном кристалле [18, 19]. Для этого необходимо сначала сделать небольшое отступление, объясняющее особенности распространения волн в анизотропном кристалле, а также показать, каким образом простое нелинейное соотношение (12.4.2) можно обобщить на случай анизотропной среды.
Можно показать, что в анизотропном кристалле в заданном направлении могут распространяться две различные линейно-поляризованные плоские волны с разными фазовыми скоростями. Этим двум различным поляризациям соответствуют два различных показателя преломления. Такое различие в значениях показателей преломления называется двулучепреломлением. Для описания этого явления обычно используют так называемый эллипсоид показателей преломления, который в случае одноосного кристалла представляет собой эллипсоид вращения вокруг оптической оси (ось г на рис. 12.5). На этом рисунке два разрешенных направления поляризации и соответствующие им показатели преломления определяются следующим образом. Через центр эллипсоида проводится прямая в направлении распространения пучка (прямая ОР на рис. 12.5) и плоскость, перпендикулярная этой прямой.
Рис. 12.5
Эллипсоид показателей преломления в положительном одноосном кристалле
Рис. 12.6
Поверхность нормалей (показателей преломления) для обыкновенной и необыкновенной волн (в положительном одноосном кристалле)
Пересечение этой плоскости с эллипсоидом образует эллипс. Две оси эллипса параллельны двум направлениям поляризации, а длина каждой из полуосей равна значению показателя преломления для данного направления поляризации. Одно из этих направлений обязательно перпендикулярно оптической оси, и волна, имеющая такое направление поляризации, называется обыкновенной. Из рисунка видно, что ее показатель преломления п0 не зависит от направления распространения. Волна с другим направлением поляризации называется необыкновенной волной, и значение соответствующего показателя преломления ле(0) зависит от угла 0 и изменяется от значения показателя преломления обыкновенной волны п0 (когда ОР параллельна оси г) до значения пе, называемого показателем преломления необыкновенной волны (когда ОР перпендикулярна оси г). Следует заметить, что положительный одноосный кристалл соответствует случаю пе > п0, а отрицательный одноосный кристалл — случаю пе < п0. Существует и другой эквивалентный метод описания распространения волн, который называется методом поверхностей нормалей (показателей преломления) для обыкновенной и необыкновенной волн (рис. 12.6). В этом случае показатель преломления волны в данном направлении распространения ОР определяется как для обыкновенной, так и для необыкновенной волн длиной отрезка до точки пересечения луча ОР с соответствующими поверхностями. Поверхность нормалей для обыкновенной волны является сферой, в то время как поверхность нормалей для необыкновенной волны представляет собой эллипсоид вращения вокруг оси г. На рис. 12.6 показаны сечения этих двух поверхностей нормалей в плоскости у ~ г для случая положительного одноосного кристалла.
После краткого обсуждения случая распространения волн в анизотропных кристаллах вернемся к вопросу индуцированной нелинейной поляризации. В общем смысле для анизотропной среды скалярное соотношение (12.4.2) уже не является справедливым, и здесь следует использовать тензорное соотношение. Запишем сначала в заданной точке г вектор электрического по-
Ля Ею(г, £) электромагнитной волны на частоте со и вектор нелинейной поляризации Р#£(г, £) на частоте 2со в виде:
Е^г, г) = (1/2)[ЕС0(г, со)ехр (усо£) + с. с.], (12.4.13а)
Р^х(г»О = (1/2)[Р2со(Г,2со)ехр (2;соО + с. с.]. (12.4.136)
При этом можно получить тензорное соотношение между величинами Р2ю(г, 2со) и Ею(г, со). Например, в направлении I кристалла компоненту поляризации второй гармоники можно записать следующим образом:
^2о>= X £о$кЕТЕк - (12.4.14)
У,*=1,2,3
Заметим, что это выражение часто записывается в следующих обозначениях: 6
(12415)
Где т пробегает значения от 1 до 6. Сокращенно эти поля записываются следующим образом:
(ЕЕ)г =Е% = Е2, (ЕЕ)2 =Е* (ЕЕ)3=Е§=Е*,
(ЕЕ)4 ^ 2Е2Е3 ^ 2ЕуЕг, (ЕЕ)Ь = 2ЕгЕ3 ^ 2ЕхЕг и (ЕЕ ^ 2ЕгЕ2 ^ 2ЕхЕу,
Где индексы как 1, 2, 3, так их, у, г обозначают оси. Заметим, что записанная в матричной форме величина <2/т является матрицей размерностью 3x6, которая действует на вектор-столбец (ЕЕ)т. В зависимости от симметрии кристалла некоторые элементы матрицы могут быть одинаковыми, а некоторые — равными нулю. В случае точечной группы симметрии 42т, к которой относятся важные нелинейные кристаллы типа КБР и халькоперитовые полупроводники, ОТЛИЧНЫМИ ОТ нуля ЯВЛЯЮТСЯ ЛИШЬ элементы <*14, ^25 и причем все они равны друг другу. Таким образом, достаточно определить только один матричный элемент <23б, и в этом случае можно записать:
Рх = 2е0(13дЕуЕ2, (12.4.16а)
Ру = 2г0(1зеЕгЕх, (12.4.166)
Рг — 2ео<13§Е ХЕ у, (12.4.16в)
Где направление оси г выбирается вдоль оптической оси одноосного кристалла. В табл. 12.1 приведены нелинейные оптические коэффициенты, классы симметрии, а также области прозрачности и пороги разрушения некоторых избранных материалов. За исключением арсенида германия - кадмия и материала А£Оа8е2, которые используются в области длин волн около 10 мкм, все остальные кристаллы применяются от ближнего УФ - до ближнего ИК-диапазонов. В таблицу также включены недавно созданные кристаллы КТР (титанил-фосфат калия) и ВВО (бетаборат бария), которые обычно применяются для генерации второй гармоники на длине волны, например, Кс1:УАС лазера. Нелинейные ^-коэффициенты, приведенные в таблице, нормированы на коэффициент для КИР, численная величина которого равна с236 = 0,5 • 10~12 м/В.
|
Нелинейные оптические коэффициенты некоторых материалов
|
В соответствии с описанием свойств анизотропной среды теперь покажем, как может быть осуществлен фазовый синхронизм для конкретного кристалла точечной группы симметрии 42т. Из выражений (12.4.16) следует, что если Ег = 0, то только поляризация Рг не обращается в нуль и, таким
|
Рис. 12.7 Угол фазового синхронизма 0ОТ в случае генерации второй гармоники типа I в отрицательном одноосном кристалле |
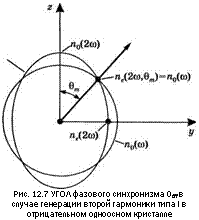 Образом, она имеет тенденцию генерировать волну второй гармоники с ненулевой г-компонентой. Напомним (см. рис. 12.5), что волна с Ег = 0 является обыкновенной, тогда как волна сЕг^О — необыкновенной. Следовательно, в этом случае обыкновенная волна на основной частоте со стремится генерировать необыкновенную волну с частотой 2со. Чтобы удовлетворить условию фазового синхронизма, основную волну можно пустить под углом 0т к оптической оси так, чтобы
Образом, она имеет тенденцию генерировать волну второй гармоники с ненулевой г-компонентой. Напомним (см. рис. 12.5), что волна с Ег = 0 является обыкновенной, тогда как волна сЕг^О — необыкновенной. Следовательно, в этом случае обыкновенная волна на основной частоте со стремится генерировать необыкновенную волну с частотой 2со. Чтобы удовлетворить условию фазового синхронизма, основную волну можно пустить под углом 0т к оптической оси так, чтобы
Тге(2со, 0т) = /г0(со). (12.4.17)
Это можно объяснить с помощью рис. 12.7, на котором показаны пересечения поверхностей нормалей я0(со) и пе(2со, 0)
с плоскостью, содержащей ось г и направление распространения. Следует заметить, что вследствие нормальной дисперсии кристалла имеет место неравенство п0(со) < п0(2со), тогда как для отрицательного одноосного кристалла имеем пе(2со) < п0(2со), где (согласно рис. 12.7) можно записать пе(2со) = пе(2со, 90°) и п0{2со) = пе(2со, 0). Отсюда следует, что «обыкновенная» окружность (для частоты со) пересекает «необыкновенный» эллипс (для частоты 2со) при некотором значении угла 0сот.[77] Для света, распространяющегося под углом 0т к оптической оси (т. е. для всех лучей, лежащих на поверхности конуса вращения вокруг оси г с углом 0т при вершине), условие (12.4.17) удовлетворяется и, следовательно, выполняется условие фазового синхронизма.
Пример 12.3. Вычисление угла фазового синхронизма для отрицательного одноосного кристалла. В соответствии с рис. 12.7, обозначим горизонтальную ось как ось у. Если теперь ввести декартовы координаты г и у для произвольной точки эллипса, описывающего показатель преломления пе(2ю, 0) необыкновенной волны, то можно записать:
У2 У2 і
Где введены следующие обозначения 7*2 - п02а)ип2 =пе(2©). Если теперь координаты г и у выразить через величину пе( 2ю, 0) и угол 0 соответственно, то предыдущее выражение можно привести к виду:
(п°2)2 (п|)
При 0 = 0т необходимо учитывать выражение (12.4.17), подстановка которого в вышеприведенное соотношение дает следующее:
К)2
|
Sin20m = 1, |
![]() (l-sin20m) + [^
(l-sin20m) + [^
I Ref
•2 У
Где снова используется запись п{ =д0(ю). Решая последнее уравнение, для переменной sin2 0m получаем:
|
1_|5L |
![]() (по2
(по2
-1
Пи - ШЛ О I
2 У
Sin20m =-
|
«І |
![]() Si - і
Si - і
Следует заметить, что если 0т * 90°, то будет иметь место дву лучепреломление, т. е. поток энергии необыкновенной волны (вторая гармоника) будет распространяться под углом, незначительно отличающимся от 0т. Таким образом, пучок основной волны и пучок волны второй гармоники будут
Распространяться в нескольких различных направлениях (хотя и удовлетворяющих условиям фазового синхронизма). Для основного пучка конечного поперечного сечения этот факт определяет верхний предел для длины взаимодействия внутри кристалла. Данное ограничение можно преодолеть, если работать с углом 0т = 90°, т. е. реализовать случай, когда пе(2со, 90°) = п0(со). Такой тип фазового синхронизма называется девяностоградусным фазовым синхронизмом, и в некоторых случаях его можно реализовать, изменяя температуру кристалла, поскольку в общем случае пе и п0 по-разному зависят от температуры. К сказанному выше можно заметить, что в отрицательном одноосном кристалле (с достаточной величиной двулучепреломления) фазовый синхронизм достижим, когда обыкновенный луч на частоте со (луч Ех в (12.4.16в)) соединяется с обыкновенным лучом, имеющим ту же частоту со (лучЕ^ в (12.4.16в)), в результате чего образуется необыкновенный луч с частотой 2со, или в соответствующих обозначениях: ою + ою —» е2(0. Этот процесс называется генерацией второй гармоники типа I. В отрицательном одноосном кристалле при наличии фазового синхронизма возможно также существование другого вида ГВГ, называемого генерацией второй гармоники типа II. В этом случае обыкновенная волна с частотой со может соединиться с необыкновенной волной, имеющей ту же частоту со, вследствие чего возникает необыкновенная волна с частотой 2со, или в соответствующих обозначе - ниях: оа + ею —> е2со.]
В настоящее время генерация второй гармоники применяется для создания когерентных источников, работающих на новых длинах волн. При этом нелинейный кристалл может быть помещен либо вне, либо внутри резонатора лазера, генерирующего основное излучение. В последнем случае с целью увеличения эффективности преобразования используется то преимущество, что внутри резонатора электромагнитное поле имеет более высокую напряженность. В обоих случая на практике была достигнута очень высокая эффективность преобразования (приближающаяся к 100%). Наиболее часто ГВГ применяется с целью удвоения частоты выходного излучения Nd:YAG лазера (когда из ИК-излучения (X = 1,064 мкм) получают зеленый свет (X = 532 нм)), а также для получения генерации перестраиваемого УФ-излучения (вплоть до X = 205 нм) путем удвоения частоты излучения перестраиваемого лазера на красителях. В обоих этих случаях в качестве источника излучения используется либо непрерывный, либо импульсный лазер. К нелинейным кристаллам, наиболее часто применяемым в качестве удвоителей частоты излучения Nd:YAG лазера, можно отнести кристаллы КТР и Я-BaB204 (ББО). Кроме того, кристалл ББО, благодаря хорошему пропусканию в УФ области спектра, применяется в случаях, когда необходимо получить генерацию второй гармоники на длине волны УФ-диапазона, вплоть до 200 нм. Другим интересным примером является эффективное преобразование частоты ИК - излучения С02 или СО лазеров с помощью халькопиритовых полупроводников (например, CdGeAs2).