ЛАЗЕРНЫЕ ПРИБОРЫ И ИХ ХАРАКТЕРИСТИКИ
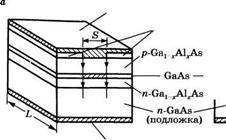
Лазеры на двойном гетеропереходе, а также лазеры на квантовых ямах весьма часто используются в конфигурации с так называемой полосковой геометрией (рис. 9.26), где активная среда (на рисунке представлена как заштрихованная область) может быть либо двойной гетероструктурой, либо структурой с раздельным ограничением и с одиночными или множественными квантовыми ямами. Из обоих рисунков можно видеть, что создание подходящего изолирующего оксидного слоя приводит к тому, что электрический ток, протекающий от положительного электрода, ограничивается в узкой полоске шириной 8 (в = 3-10 мкм). По сравнению с устройствами на широких переходах (см. рис. 9.20) рассмотренное устройство с полосковой геометрией имеет в качестве преимущества значительно меньшую площадь перехода Л (А = Ьв, где Ь — длина полупроводника), через который протекает ток. Таким образом, для заданной плотности токае/ требуемый полный ток I = JA соответственно оказывается меньше. Кроме того, поскольку ширина области усиления в плоскости перехода приблизительно равна ширине 8, этот механизм можно использовать для ограничения поперечного размера пучка в направлении, параллельном переходу. Соответствующее устройство называется лазером на активной волноводной структуре, т. е. сформированной путем распределения усиления (см. рис. 9.26а). Если сделать ширину в достаточно малой (в < 10 мкм), то ограничение усиления приведет к тому, что пучок ограничится основной поперечной модой в направлении, параллельном переходу. С другой стороны, в направлении, перпендикулярном переходу, пучок также ограничится основной поперечной модой, но уже за счет распределения показателя преломления в двойной волноводной гетероструктуре (см. рис. 9.22) или в структуре с раздельным ограничением (см. рис. 9.24). Таким образом, выходной пучок будет состоять из одной поперечной моды с эллиптическим профилем сечения пучка (размер -1x5 мкм). Недостатком активной волноводной структуры (рис. 9.26а) является то, что невозбужденные области активного слоя очень сильно поглощают излучение, и ограничение пучка в этих областях неизбежно приводит к дополнительным потерям.
|
Металлический контакт (—)' |
|
Рис. 9.26 Фрагмент полупроводникового ДГ-лазера с полосковой геометрией: а) лазер с активной волноводной структурой, б) лазер со скрытой гетероструктурой и распределенным коэффициентом преломления. |
|
|||||||
|
|||||||
|
|||||||
 |
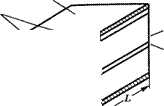
Лучшим решением в этом случае было бы обеспечить боковое ограничение за счет распределения показателя преломления в плоскости перехода (лазеры на пассивной волноводной структуре с распределенным показателем преломления). В качестве возможного решения можно окружить активный слой полупроводниковыми материалами с более низким показателем преломления, как например в лазерах со скрытой гетероструктурой (рис. 9.266). Преимуществом лазера с пассивной волноводной структурой является то, что лазерный пучок в этом случае испытывает меньшее поглощение в боковых ограничивающих средах. В действительности, пассивные волноводные структуры с распределенным показателем преломления (например, скрытые или гребенчатые волноводные структуры) представляются сейчас наиболее перспективными для серийно выпускаемых устройств.
|
Ток I (мА) Рис. 9.27 График зависимости выходной мощности от электрического тока в ДГ-лазере при двух значениях температуры |
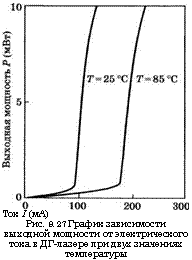 Теперь можно рассмотреть некоторые свойства выходного пучка, а именно: выходную мощность, расходимость пучка и его спектральный состав. На рис. 9.27 представлен график зависимости выходной мощности от электрического тока при двух значениях температуры для ДГ-GaAs лазера на волноводной структуре. Следует отметить, что снижение порогового тока Ith до значений 100 мА и ниже при комнатной температуре стало возможным в результате использования структур с полосковой геометрией. На сегодняшний день достигнуты еще меньшие пороговые токи (-15 мА) благодаря использованию ДГ-GaAs лазеров на активной и пассивной волноводных структурах. Рекордно малые значения порогового тока (-1 мА) реализованы с помощью одиночных квантовых ям. (Действительно, полагая Jth = 200 А/см2, (см. пример 9.2), s = 4 мкм и L = 150 мкм, можно получить Ith = 1,2 мА.) Из рис. 9.27 также видно, что величина Ith резко возрастает с ростом температуры. Эмпирическим путем было показано, что для большинства лазерных диодов эта зависимость подчиняется закону Ith ос ехр (Т/Т0), где Т0 — характерная температура, зависящая от параметров того или иного лазерного диода, и значение которой является мерой качества диода. Действительно, отношение пороговых значений для двух различных температур, отличающихся на величину АТ, задается выражением (Цк /I”h) = ехр(ДТ/Т0). Таким образом, чем больше параметр Т0, тем в меньшей степени величина Ith чувствительна к температуре. Для случая, изображенного на рис. 9.27, можно оценить, что Т0 = 91 К. Как правило, в ДГ-GaAs лазерах величина Т0 лежит в диапазоне 100-200 К, причем для GaAs лазеров на квантовых ямах этот параметр оказывается несколько больше (> 270 К). Таким образом, улучшение в плане температурных характеристик лазеров на квантоворазмерных структурах является еще одним преимуществом таких
Теперь можно рассмотреть некоторые свойства выходного пучка, а именно: выходную мощность, расходимость пучка и его спектральный состав. На рис. 9.27 представлен график зависимости выходной мощности от электрического тока при двух значениях температуры для ДГ-GaAs лазера на волноводной структуре. Следует отметить, что снижение порогового тока Ith до значений 100 мА и ниже при комнатной температуре стало возможным в результате использования структур с полосковой геометрией. На сегодняшний день достигнуты еще меньшие пороговые токи (-15 мА) благодаря использованию ДГ-GaAs лазеров на активной и пассивной волноводных структурах. Рекордно малые значения порогового тока (-1 мА) реализованы с помощью одиночных квантовых ям. (Действительно, полагая Jth = 200 А/см2, (см. пример 9.2), s = 4 мкм и L = 150 мкм, можно получить Ith = 1,2 мА.) Из рис. 9.27 также видно, что величина Ith резко возрастает с ростом температуры. Эмпирическим путем было показано, что для большинства лазерных диодов эта зависимость подчиняется закону Ith ос ехр (Т/Т0), где Т0 — характерная температура, зависящая от параметров того или иного лазерного диода, и значение которой является мерой качества диода. Действительно, отношение пороговых значений для двух различных температур, отличающихся на величину АТ, задается выражением (Цк /I”h) = ехр(ДТ/Т0). Таким образом, чем больше параметр Т0, тем в меньшей степени величина Ith чувствительна к температуре. Для случая, изображенного на рис. 9.27, можно оценить, что Т0 = 91 К. Как правило, в ДГ-GaAs лазерах величина Т0 лежит в диапазоне 100-200 К, причем для GaAs лазеров на квантовых ямах этот параметр оказывается несколько больше (> 270 К). Таким образом, улучшение в плане температурных характеристик лазеров на квантоворазмерных структурах является еще одним преимуществом таких
устройств и ведет к более слабой зависимости энергии квазиуровней Ферми и соответственно зависимости дифференциального усиления от температуры (для сравнения, рис. 3.25 и рис. 3.15). Характерная температура в ДГ-лазерах на 1пОаАвР/1пР-структурах оказывается значительно меньше, чем значения, рассмотренные выше (50 К < Т0 <70 К), вероятно из-за резкого увеличения скорости безызлучательной релаксации (вследствие Оже- рекомбинации) в таких более узкозонных материалах (см. раздел 3.2.6). Следует отметить, что выходная мощность (см. рис. 9.27) ограничена сверху значением -10 мВт. Более высокие выходные мощности (обычно более 50 мВт) могут привести к тому, что интенсивность пучка станет достаточно высокой и сможет превысить порог разрушения поверхности полупроводника. Окончательно отметим, что дифференциальный КПД лазера задается выражением г)^ = <2Р/У<2/, где V — приложенное напряжение. Выбирая V = 1,8 В, получаем г)з = 40%. В действительности были получены более высокие значения дифференциального КПД (вплоть до 60%). Таким образом, в настоящий момент полупроводниковые лазеры являются наиболее эффективными из всех известных типов лазеров.
Пример 9.3. Выходная мощность и внешняя квантовая эффективность полупроводниковых лазеров. Чтобы рассчитать выходную мощность, отметим вначале, что в стационарных условиях величину мощности вынужденного излучения можно записать в виде: Ре = (1 - 1*л)г|£Лу/е, где г]* — внутренняя квантовая эффективность, введенная в разделе 9.4.3, и V — частота испускаемого излучения. Часть этой мощности тратится на внутренние потери (вследствие рассеяния, а также из-за потерь во внешних слоях), а часть мощности выходит через торцевые зеркала. Таким образом, мощность пучка можно выразить следующим образом:
|
|
(9.4.14)
Где і? — коэффициент отражения зеркал, а — коэффициент внутренних потерь и Ь — длина резонатора. Теперь можно определить внешнюю квантовую эффективность гех как отношение приращения количества испускаемых фотонов к соответствующему приращению инжектированных носителей зарядов, т. е. гех = (і(Р/Іі)/(і(І/е). Тогда из выражения (9.4.14) получаем:
|
|
(9.4.15)
Отсюда видно, что величина гех растет с уменьшением длины резонатора. Следует также отметить, что согласно определенным величинам соотношение между внешней квантовой эффективностью и дифференциальным КПД записывается в виде хех = х3(еУ/Н').
Что касается расходимости выходного излучения, отметим, что из-за малых размеров пучка (-1 мкм) в направлении, перпендикулярном переходу, выходной пучок в этой плоскости будет всегда дифракционно-ограниченным.
Более того, как уже отмечалось выше, если ширина полоски в гетероструктуре оказывается меньше некоторого критического значения (-10 мкм), то пучок будет дифракционно-ограниченным и в плоскости, параллельной переходу. Теперь положим размеры пучка равными й± и <2ц (полная ширина на уровне 1/е поля) по обоим направлениям, и предположим, что распределение поля имеет гауссов профиль в обоих поперечных направлениях. Согласно выражению (4.7.19), расходимость пучка в плоскости, параллельной переходу (0ц), и в плоскости, перпендикулярной переходу (0^, задается соответствующими выражениями 0ц = 2'к/к(1\ и 0± = 2Х/пй±. Для выходного луча с эллиптическим поперечным сечением (например, 1x5 мкм) расходимость в плоскости, перпендикулярной переходу, будет больше, чем расходимость в плоскости, параллельной переходу. Далее, уже на расстоянии нескольких десятков микрометров от выходного торца полупроводника (см. рис. 6.9а) эллиптичность пучка поворачивается на 90°. Как уже было показано в разделе 6.3.2.1, для компенсации астигматизма пучка можно разработать специальные оптические системы.
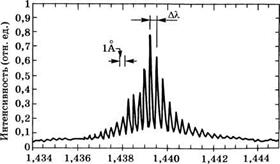
На рис. 9.28 представлен типичный спектр излучения диодного лазера, в котором оптическая обратная связь обеспечивается за счет отражения на торцевых зеркалах. Равноудаленные пики на графике соответствуют различным продольным модам резонатора Фабри-Перо. Из этого рисунка можно сделать два вывода:
1. Относительная спектральная ширина линии Ау^/у достаточно мала (-1,1 • 10_3), что доказывает утверждение, согласно выражению (9.4.1), о том, что частота излучения приблизительно равна величине Её/к.
2. Абсолютное значение ширины линии Ауь = 400 ГГц (см. рис. 9.28) оказывается достаточно большим, что является серьезной проблемой в устройствах оптической связи вследствие хроматической дисперсии оптического волокна (особенно вблизи длины волны А, = 1550 нм). Чтобы обеспечить много меньшую ширину линии желательно использовать лазер с распределенной обратной связью или лазер с распределенным брэгговским отражением. Эти лазеры будут кратко рассмотрены в следующем разделе.
|
Энергия, /го (эВ) Рис. 9.28 Типичный спектр излучения СаАв полупроводникового ДГ-лазера со структурой типа Фабри-Перо с длиной резонатора 250 мкм |