ПРИНЦИПЫ ЛАЗЕРОВ

ТЕОРИЯ АКТИВНОЙ МОДУЛЯЦИИ ДОБРОТНОСТИ

Для простоты ограничимся рассмотрением лишь активной модуляции добротности и в дальнейшем будем считать, что переключение добротности происходит мгновенно (быстрое переключение) [12]. Для описания проис­ходящих в лазере процессов можно снова воспользоваться уравнениями

(7.2.16) и (7.2.24) соответственно для четырехуровневого и квазитрехуров - невого лазеров.

Рассмотрим сначала четырехуровневый лазер, работающий в импульсном режиме (рис. 8.9), и предположим, что при £ < 0 потери столь велики, что ла­зер работает в допороговом режиме. Если модуляция добротности происходит в момент времени, когда 7У(£) достигает максимального значения, то соответ­ствующую начальную инверсию можно получить из уравнения (7.2.16а), по­лагая (йИ/М) = 0. Таким образом, имеем:

ЛГ* = тЯр(0), (8.4.6)

Где Яр(0) — значение скорости накачки в момент времени £ = 0 (т. е. в момент переключения добротности). Предположим теперь, что зависимость Яр(Ь) от времени имеет всегда один и тот же вид, независимо от величины интеграла

|#рс/£, т. е. от энергии накачки. Тогда можно положить #р(0)= ]#рс?£, так

Что, например, если удваивается |Ярс££, то удваивается также и #р(0). Та­ким образом, если Ер — энергия накачки, соответствующая данной скорости накачки (поскольку Ер ос |Ярс££), то далее имеем Ер ос Яр(0) и согласно соот­ношению (8.4.6) получаем Ер осЛ^. Следовательно, обозначив как Л^с и£рс начальную инверсию и соответствующую энергию накачки при работе лазе­ра на пороге генерации, можно записать:

(М1/М1с) = (Ер/Ерс) = х, (8.4.7)

Где х = (Ер/Ерс) — значение превышения накачки над порогом. Поскольку Л^с — это просто критическая инверсия для данного лазера (в режиме моду­ляции добротности, когда затвор открыт), ее значение можно получить из обычного соотношения для критической инверсии, т. е. Л^с = Ыс = у/а/, где у — потери в резонаторе при открытом затворе. Если известна величина Л^с, т. е. известны у, а и /, и если также известно отношение х энергии накачки и пороговой энергии накачки, то выражение (8.4.7) позволяет найти началь­ную инверсию

Теперь, после того как известно значение Л^, эволюцию системы во вре­мени после включения добротности (т. е. при £ > 0) можно описать уравнени­ем (7.2.16) с начальными условиями ЛГ(0) = и ф(0) = ф*. Здесь вновь ф* — небольшое число фотонов, необходимое для того, чтобы началась лазерная генерация (ф* =1). Эти уравнения можно существенно упростить, поскольку ожидается, что изменения во времени величин ЛГ(£) и ф(£) происходят за столь короткие промежутки времени, что в уравнении (7.2.16а) можно пренебречь членом #р, отвечающим за накачку, и членом ЛГ/т, отвечающим за релакса­цию. Тогда уравнения (7.2.16) сводятся к следующему виду:

— = -ВфЛГ, (8.4.8а)

|=(г„ВА,-А)ф. (8.4.86)

Прежде чем продолжить дальнейшее рассуждение, следует напомнить, что согласно (8.4.86) населенность Ыр, соответствующая максимуму светово­го импульса (см. рис. 8.9в), т. е. когда (йф/(И) = 0, дается выражением:

Ыр=1/УаВтс = у/а1, (8.4.9)

Которое в точности совпадает с выражением для критической инверсии Ыс. Этот результат с учетом выражения (8.4.7) позволяет записать отношение Л^/#р в виде, удобном для дальнейшего рассмотрения:

(М1/Нр) = х. (8.4.10)

Сделав эти предварительные замечания, можно перейти к вычислению пиковой мощности импульса Рр, выходящего из лазера через, например, зер­кало 2. Согласно (7.2.18) имеем:

РР =(|!г)Лл'Фр’ (8.4.11)

Где фр — число фотонов в резонаторе в тот момент времени, когда лазерный импульс достигает пикового значения. Для вычисления фр разделим уравне­ние (8.4.86) на (8.4.8а). Учитывая также соотношение (8.4.9), получаем сле­дующее уравнение: г

/1/К

■-у„

(8.4.12)

Проинтегрировав которое, нетрудно получить

Ф = Уа[Ы1 - N - ЛГр1п (ЛГ,/ЛГ)], (8.4.13)

Где для простоты мы пренебрегли небольшим числом ф,-. Тогда в максимуме импульса имеем:

(8.4.14)
Откуда можно сразу получить величины фр, если известны Np (из (8.4.9)) и отношение (Ni/Np) (из (8.4.10)). Теперь из формул (8.4.11), (8.4.14) и (8.4.9) можно вычислить пиковую выходную мощность:

(8.4.16)

Где Р(£) — выходная мощность как функция времени и где вновь использова­лось выражение (7.2.18). Интегрирование в выражении (8.4.16) нетрудно выполнить, если проинтегрировать обе части уравнения (8.4.86) и заметить,

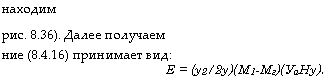Что ф(0) = ф(оо) ^ 0. Далее получаем ф<2£ = Уахс £° В^ЫсИ. Интеграл ВфМ2£ можно теперь вычислить, интегрируя обе части уравнения (8.4.8а), откуда МсН = (Л^ - Nf ), где — конечная инверсия населенностей (см.

& = УатсСЭД - N^1 и, таким образом, выраже-

(8.4.17)

Смысл этого выражения нетрудно понять, если заметить, что величина (N1 - Л^) — это имеющаяся в наличии инверсия, которая дает число фотонов (Л^-ЛТг)Уа. Из этого числа фотонов, испущенных активной средой, лишь доля (у2/2у) фотонов дает вклад в выходную энергию. Чтобы вычислить £ с помощью выражения (8.4.17), необходимо знать Л/^. Эту величину можно получить из выражения (8.4.13), полагая в нем / —> оо. Поскольку ф(оо)^Г получаем соотношение:

Nt

Nt Nt

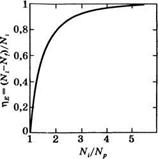
Которое дает Nf/Nt как функцию величины Np/Ni. Теперь можно опреде­лить величину г)я = (Nt - Nf)/Nt, которая стоит в левой части выражения

(8.4.18) , как коэффициент использования инверсии (или энергии). Дейст­вительно, хотя начальная инверсия равна Nu фактически используется лишь разность (Nt - Nf). В обозначениях гЕ выражение (8.4.17) можно пе­реписать в следующем виде:

Ле(^/^) = -1п(1-Ле). (8.4.19) На рис. 8.11 построена кривая зависимо­сти коэффициента использования энергии гЕ от величины (^/ЛГр), полученная вычислени­ем выражения (8.4.19). Заметим, что при боль­ших значениях (NІ/Nр), т. е. когда энергия накачки намного превосходит пороговую энер­гию накачки, коэффициент использования энергии стремится к единице. Заметим так­же, что в обозначениях гЕ и с помощью (8.4.9) выражение (8.4.17) можно представить в бо­лее простом и наглядном виде:

Рис. 8.11 Коэффициент использования энергии г|£ в зависимости от отношения начальной инверсии к пиковой

(8.4.20)

Где снова Аъ = Уа/1 — площадь сечения пучка.

Если известны выходная энергия и пиковая мощность, то можно найти приближенное значение длительности импульсов Атр, определив его с помо­щью соотношения Дтр = Е/Рр. Из выражений (8.4.20) и (8.4.15) получаем:

' KN,/Np)-IniN, /Np)-iy

Заметим, что отношение Атр/тс зависит только от величины (Ni/Np) = х, и для диапазона (Ni/Np), например от 2 до 10, значение Атр будет в 5,25 -

- 1,49 раз больше времени жизни фотона в резонаторе тс. В частности, для (Ni/Np) = х = 2,5 из рис. 8.11 получаем гЕ = 0,89, а из выражения (8.4.21) находим Атр = 3,81тс. Однако следует заметить, что выражение (8.4.21) дает лишь приближенное значение Атр. Излучаемый импульс является несиммет­ричным, поскольку длительность его переднего фронта тг всегда меньше дли­тельности заднего фронта xf. Например, если определить тг и xf как интервалы времени от пиковой мощности импульса до моментов времени, соответствую­щих половине пиковой мощности, то численный расчет для (Ni/Np) = х = 2,5 дает значения тг= 1,45тс и xf= 2,06тс. Отсюда видно, что в данном примере вычисленное при помощи соотношения (8.4.21) приближенное значение Атр примерно на 9% превышает расчетное значение xr - I - т^. Полученное соотно­шение приближенно выполняется для любого (Ni/Np).

Теперь можно рассчитать время задержки между максимумом импуль­са и моментом включения добротности (см. рис. 8.9). Эту задержку можно считать равной времени, которое необходимо для того, чтобы число фото­нов достигло определенной величины относительно максимального числа фотонов. Если выбрать, например, эту долю равной (1/10), то до этого мо­мента времени не произойдет сколько-нибудь заметного насыщения инвер­сии, и в уравнении (8.4.86) можно воспользоваться приближением Тогда это уравнение с учетом соотношений (8.4.9) и (8.4.10) принимает вид (с/ф/^£) = (х — 1)ф/тс, и после интегрирования имеем:

Ф = Ф/ ехр[(д: — 1)£/тс].

Подставляя сюда ф = фр/10, находим время задержки та. Полагая ф* = 1, получаем:

(8.4.23)

Где фр дается выражением (8.4.14). Заметим, что поскольку фр очень большое число (» 1017 или больше, см. следующий пример) и поскольку в выражении

(8.4.23) оно стоит под знаком логарифма, величина не изменилась бы су­щественно, если вместо фр/10, например, выбрать фр/20.

Пример 8.4. Выходная энергия, длитель­ность импульса и время нарастания им­пульса в обычном Ий.’УАЄ лазере с модуля­цией добротности. На рис. 8.12 представле­на типичная зависимость выходной энергии лазера Е от подводимой к лампе энергии накачки Ер для К(1:УАО лазера с модуля­цией добротности. На вставке этого рисун­ка также указаны размеры стержня и ре­зонатора [13]. Лазер работает в импульсном режиме, и модуляция добротности в нем осуществляется с помощью кристалла КБ*Р (дейтерированный дигидрофосфат калия, КХ>2Р04) в ячейке Поккельса. Из рисунка вид­но, что пороговая энергия лазера составляет Еср = 3,4 Дж, а энергия выходного излучения Е = 120 мДж при Ер = 10 Дж. Найденная из измерений длительность импульса лазера при этой накачке составляет около 6 не.

Теперь можно сравнить эти эксперимен­тальные данные с результатами расчетов по формулам, приведенным в предыдущем раз­деле. Пренебрежем поглощением в зеркалах И ПОЛОЖИМ у2 = -1п /?2 = 1,2 И У! = 0. Согласно оценкам, в системе поляризатор — ячейка Поккельса внутренние потери составляют Ьі = 15%, а внутренними потерями в стерж­

Не можно пренебречь. Таким образом, получаем yt = - ln(l - Lt)^ 0,162 и у = [(уг + у2)/2] + yt = 0,762. Расчетное значение энергии лазера (при = = 10 Дж) можно получить из выражения (8.4.20), если заметить, что в этом случае (Ni/Np) = (Ер/Еср) = 2,9. Теперь положим АЬ=А = 0,19 см2, где А — площадь поперечного сечения лазерного стержня. Поскольку (Ni/Np) = 2,9, из рис. 8.11 находим, что = 0,94, а из выражения (8.4.20), полагая, что эффективное сечение вынужденного излучения равно а = 2,8 • 10~19 см2 (см. пример 2.10), получаем Е = 200 мДж. Иногда теоретические расчеты дают несколько большее значение, и это связано с двумя причинами:

1. Площадь поперечного сечения пучка определенно меньше, чем стержня.

2. Из-за небольшой длины резонатора не выполняется условие быстро­го включения добротности резонатора (т. е. требование, что время пере­ключения добротности должно быть намного меньше времени нарастания лазерного импульса). Ниже в этом примере будет показано, что действи­тельно расчетное время нарастания модулирующего импульса (время за­держки) та составляет около 20 не. Достаточно трудно переключить ячейку Поккельса за более короткое время, и, как следствие, во время переключе­ния часть энергии будет теряться при прохождении через поляризатор (в не­которых типичных случаях при такой короткой длительности в процессе модуляции на выход проходит только 20% энергии).

Прежде чем вычислять длительность импульса, необходимо отметить, что согласно выражению (7.2.11) эффективная длина резонатора определя­ется как Le = L +(п-1)1 = 22 см, где п = 1,83 для кристалла Nd:YAG, таким образом, из (7.2.14) получаем тс = Le/cy= 1 не. Длительность лазерного им­пульса определяется из выражения (8.4.21): Атр = хстЕх/(х - ln х - 1) = 3,3 не (при этом для расчета можно использовать рис. 8.11). Различие между расчетным и экспериментальным (Дтр = 6 не) значениями можно объяснить двумя следующими причинами:

1. Многомодовый режим генерации. Действительно, время нарастания импульса различно для разных мод в силу незначительного отличия их коэффициентов усиления. В результате заметно увеличивается длитель­ность импульса.

2. Как уже упоминалось, в данном случае полностью не выполняется условие быстрого включения добротности резонатора и, по-видимому, мед­ленное включение добротности приводит к некоторому увеличению дли­тельности лазерного импульса.

Время нарастания импульса при переключении добротности может быть получено из выражения (8.4.23), если известно значение фр. Теперь если взять Np = у/Ы = 5,44 • 1017 см-3 и положить, что Va=Abl=Al=l см3, из формулы (8.4.14) получаем фр s 4,54 • 1017 фотонов, так что из выраже­ния (8.4.23), при тс = 1 не и х = 2,9, находим та = 20 не.

Пример 8.5. Динамическое поведение Nd:YAG лазера с пассивной мо­дуляцией добротности. Рассмотрим лазерный резонатор, эффективная дли­на которого составляет Le = 50 см и в котором в качестве активной среды используется стержень из Nd: YAG, диаметр стержня равен D — 5 мм. Пусть в лазере используется пассивная модуляция добротности, реализуемая с помощью ячейки с насыщающимся поглотителем, интенсивность насыще­ния которого составляет I8= 1 МВт/см2. Предположим также, что ячейка
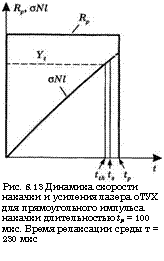
с раствором насыщающегося поглотителя обладает потерями (до возникновения насы­щения) равными Ь = 50%. Пусть коэффи­циент отражения выходного зеркала равен Я2 = 74%, а всеми прочими потерями в ре­зонаторе можно пренебречь. Таким обра­зом, имеем у2 = -1п#2 = 0,3 для потерь на выходном зеркале (связь на выходе) иуа = = -1п (1 —Ь) = 0,693 для потерь поглотителя без насыщения. Тогда полные потери до мо­мента насыщения составляют = уа + (у2/2) = = 0,843. Теперь предположим, что накачка осуществляется прямоугольными импульса­ми длительностью = 100 мкс(см. рис. 8.13). Согласно выражению (8.4.1) инверсия насе­ленностей в конце импульса накачки и до мо­мента возникновения лазерной генерации определяется как

= ЫЛ1 - ехр(-*Р/т)] = 0,35^, (84.24)

Где х = 230 мкс. Порог генерации будет достигнут за время tth (см. рис. 8.13), так что:

АЩ^ь)1 = у,. (8.4.25)

Теперь предположим, что уровень накачки превышает пороговое зна­чение на 10%, таким образом:

ЛГ(*р)=1,Ш(*4Л), (8.4.26)

Где ЛГ(£р) — инверсия населенностей в момент времени t = tp при отсутст­вии генерации (см. рис. 8.13). Из выражений (8.4.26) и (8.4.24) находим Л^(£еЛ) = 0,32ЛГо0. Далее, из (8.4.1) получаем tth = 88 мкс, а из (8.4.25) имеем = у,/0,32 = 2,64.

При t > лазер обладает полным усилением £пс*(£')> которое, до мо­мента существенного насыщения поглотителя, можно описать уравнением: 8пе№ = оМ-у( = с 1(йН’/йЛн?1 где введена новая временная ось? с началом координат в точке £ = Из выражения (8.4.1) и с учетом полученного выше

Значения **Л, имеем (йЫ/йг)^ = (Ы^/техр (-^А/т) = 0,68(Мао/т). Отсюда полу­чаем выражение для полного усиления ёпеА?) = 0,68(аА^оо0(£7'г) и, учитывая полученное выше значение (аЛГ^), находим:

§пег(Г)= 1,8(Г/т). (8.4.27)

Имея выражения для полного коэффициента усиления, можно описать динамику увеличения числа фотонов в резонаторе с помощью следующего уравнения:

№/М) = (ёпе1ЦТЦ9 (8.4.28)

Где = Ье/с ^ 1,66 не — время одного прохода пучка через резонатор. Урав­нение (8.4.28) можно разрешить для аргумента, очень похожего на тот, который был получен для уравнения (7.2.12). Если выражение (8.4.27) подставить в (8.4.28) и затем проинтегрировать полученное уравнение, то можно записать:

Следует отметить, что поскольку полное усиление растет линейно от времени (см. (8.4.27)], то в этом случае функция ф(£') будет расти экспонен­циально с ростом величины t'2 (см. (8.4.29), а также рис. 8.8а, где для этого примера время t совпадает с временем t'). Для того чтобы рассчитать с помощью выражения (8.4.29) время при котором наступает насыще­ние, необходимо связать функцию ф(£') с периодично изменяющейся ин­тенсивностью пучка 1(f). Для этого вначале следует отметить, что если два пучка с одинаковой интенсивностью I распространяются внутри резонато­ра в противоположных направлениях, то пространственно усредненное зна­чение плотности энергии в резонаторе будет равно р = 21/с (ср. с (2.4.10)). Таким образом, связь между числом фотонов и интенсивностью излучения внутри резонатора будет иметь вид: ф = рA^Jhv = 2IAbLe/chv, гдеАъ — пло­щадь поперечного сечения пучка. Из предыдущего выражения, выбирая Аъ = я£>2/4 = 0,196 см2, находим, что число фотонов фя, соответствующее интенсивности насыщения Ia= 1 МВт/см2, составляет фв = 3,49 • 1015. Из (8.4.29), принимая ф* = 1, получаем (t's/tT) = 2,347, т. е. t’s = 3,89мкс и, сле­довательно, t8 = 92 мкс (см. рис. 8.13). Таким образом, начиная с некоторого уровня шумов и через количество проходов -2350 можно достичь интенсив­ности, равной интенсивности насыщения поглотителя. И с этого момента просветление насыщающегося поглотителя наступает очень быстро.

Таким образом, при t>ts динамическое поведение лазера может быть приближенно рассчитано уже с учетом полного просветления поглотите­ля. Опираясь на уравнения, рассмотренные в данном разделе, можно по­строить зависимости величин от времени, предполагая, что начальная инверсия равна Nt = N(t8). Теперь можно рассчитать начальное усиление лазера, равное gt = - ехр-(£я/т)] = 0,87, тогда как усиление

В максимуме импульса составляет gp = cNpl = у = 0,15. Откуда получаем Ni/Np = gjgp = 5,8. Полная инверсия населенностей в объеме Va отдельной моды задается выражением Nya = NjAbl = (Ab/c)gi. Принимая а = 2,8 • 10~19 см2 (см. предыдущий пример) и предварительно рассчитав величины Аъ и gi9 находим Nya = 6,09 • 1017 ионов (см. рис. 8.86). Аналогично находим NpVa = = NiVa/598 = 1,05 • 1017 ионов. Максимальное число фотонов можно найти из (8.4.14), и здесь имеем фр = 3,191017 фотонов. Время задержки xd (от­носительно максимума импульса) и ширина импульса Лтр находятся из вы­ражений (8.4.23) и (8.4.21) соответственно, если рассчитать время жизни фотона в резонаторе как тс = tT/у =11 не. В результате получаем та = 88 не, и Атр = 21 не и, таким образом, максимум импульса будет иметь место при­близительно через время t'p =t's+xd +(Дтр/2) = 3,99мкс (рис. 8.86).

Рассмотрим теперь импульсно-периодический лазер с модуляцией доб­ротности при непрерывной накачке (рис. 8.10). Прежде всего заметим, что после включения добротности и в течение формирования импульса модуля­ции добротности все еще применимы уравнения (8.4.8). Следовательно, пико­вая выходная мощность, выходная энергия и длительность импульса даются выражениями (8.4.15), (8.4.20) и (8.4.21) соответственно. Однако отношение
(N1/Ир) уже не определяется выражением (8.4.10), поскольку в этом случае динамика накачки изменилась. Действительно, потребуем теперь, чтобы за время тр между двумя последующими импульсами накачка восстанавливала начальную инверсию, начинающуюся с некоторого значения населенно­сти Ир которая оставалась после предшествующего переключения доброт­ности. Интегрируя уравнение (7.2.16а) и полагая ф = 0, получаем:

Nt = (Rpx) - (RpT- Nf)exp (-тр/т).

Из соотношений (7.3.6), (7.3.3) и (8.4.9) имеем: Rpx = xNc выражение (8.4.30) приводит к следующему уравнению:

N,

Ехр(-1//*)] = !- “ехр(-1/ Г),

Где х — превышение уровня непрерывной накачки над пороговым значени­ем, а = где f= 1/тр— нормированная частота повторения импульсов лазера. Уравнения (8.4.31) и (8.4.18) (последнее по-прежнему справедливо! составляют систему двух уравнений, которые позволяют вычислить (Ni/Np) и (NJNf), если известны х и /*.

На рис. 8.14 приведены полученные таким образом зависимости величин ны (Ni/Np) от величины х превышения накачки над порогом для нескольким значений нормированной частоты /*. Для данных значений xuf*c помощью рис. 8.14 можно определить соответствующее значение (Nt /Np). Определив (Nt /Np), из рис. 8.11 находим коэффициент использования энергии гЕ. Те­перь, если известны (N^Np) и г|£, то из выражений (8.4.15), (8.4.20) и (8.4.21) нетрудно вычислить соответственно Рр, Е и Лтр. Заметим, что в пределах рас­сматриваемых значений х и /* зависимость между (Nt /Np) и х близка к ли­нейной.

Расчеты для квазитрехуровневого лазера проводятся аналогичным обра­зом, при этом вычисления начинаются с рассмотрения уравнений (7.2.24). Вследствие ограничений на объем книги эти расчеты здесь не приводятся.