ЗАТЯГИВАНИЕ ЧАСТОТЫ И ПРЕДЕЛ МОНОХРОМАТИЧНОСТИ
Предположим, что генерация осуществляется на моде резонатора с частотой ус, которая отличается от центральной частоты перехода у0. Пусть Дус — ширина резонансной моды и Ду0 — ширина лазерного перехода. Необходимо найти частоту генерации уь и ширину линии выходного спектра Ауь (рис. 7.27).
Величину у£ можно вычислить в рамках полуклассического приближения. В работах [3, 22] показано, что равна некоторому промежуточному значению между у0 и ус, т. е. частота генерации затягивается по направлению к центральной частоте лазерного перехода у0. Для неоднородно уширенной линии частота генерации в первом порядке приближения (и точно для однородно уширенной линии) определяется средним взвешенным двух частот: у0 и ус, при этом весовые множители оказываются обратно пропорциональными соответствующим ширинам линий. Таким образом, имеем:
|
(7.9.1) |
![]() (у0/Ау0) + (ус/АуС)
(у0/Ау0) + (ус/АуС)
VI, =
(1/Ду0)+(1//Аус) ’
Затягивание частоты, как правило, очень мало. Величина Ду0 может иметь значения в пределах ~1 ГГц для доплеровски уширенного перехода в видимой области спектра и до 300 ГГц в твердотельных лазерах (см. табл. 2.1). С другой стороны, для резонатора длиной 1 м величина Дус = 1/2птс = ус/2пЬе [см. (7.2.14) и (5.3.10)] может принимать значения от ~1 МГц до нескольких десятков мегагерц (в случае, когда у изменяется в пределах от ~1%, что является типичным для лазеров с низким коэффициентом усиления, например для Не-Ые лазера, до значения ~50% для активных сред с высоким усилением). Таким образом, нетрудно видеть, что весовой фактор (1/Дус) более чем на три порядка величины превышает значение (1/Ду0).
|
Линия лазерного перехода |
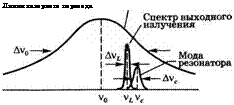 Обратимся теперь к расчету ширины Ауь спектра выходного излучения лазера, когда генерация в нем осуществляется лишь на указанной выше моде. Наименьшее значение ширины определяется шумами спонтанного излучения или, более точно, нулевыми флуктуациями поля лазерной моды. Поскольку эти флуктуации можно учесть лишь с помощью полного квантовомеханического рассмотрения (см. раздел 2.3.2), определить эту предельную ширину в рамках используемого здесь приближения не представляется возможным. Можно показать, что хотя случайным флуктуациям подвержены и амплитуда, и фаза поля нулевых колебаний, спектральное уши - рение выходного излучения обусловлено главным образом случайными флуктуациями фазы, тогда как очень небольшие флуктуации величины выходной мощности вызваны флук-
Обратимся теперь к расчету ширины Ауь спектра выходного излучения лазера, когда генерация в нем осуществляется лишь на указанной выше моде. Наименьшее значение ширины определяется шумами спонтанного излучения или, более точно, нулевыми флуктуациями поля лазерной моды. Поскольку эти флуктуации можно учесть лишь с помощью полного квантовомеханического рассмотрения (см. раздел 2.3.2), определить эту предельную ширину в рамках используемого здесь приближения не представляется возможным. Можно показать, что хотя случайным флуктуациям подвержены и амплитуда, и фаза поля нулевых колебаний, спектральное уши - рение выходного излучения обусловлено главным образом случайными флуктуациями фазы, тогда как очень небольшие флуктуации величины выходной мощности вызваны флук-
Туациями амплитуды ПОЛЯ нулевых Затягивание частотой спектр выходного Колебаний. Это МОЖНО объяснить, излучения в одномодовом лазере
Обращаясь к тому факту, который рассматривался в начале данной главы, что количество фотонов в резонаторе лазера, а следовательно, и выходная мощность весьма нечувствительны к тому числу фотонов ф;, которые изначально имеются в резонаторе, чтобы вызвать процесс спонтанного излучения. Для большей точности можно показать, что согласно уравнению (7.2.2), скорость увеличения числа фотонов в резонаторе за счет «дополнительного» фотона, возникающего в результате спонтанного излучения, определяется для стационарного состояния выражением (d§/dt)se = VaBN0; данное соотношение необходимо сравнить с выражением для вынужденного излучения, которое, также согласно уравнению (7.2.2), имеет вид VaBN0ф0. Поскольку ф0 может лежать в диапазоне от Ю10 до 1016 (см. пример 7.1), очевидно, что множитель, отвечающий за спонтанное излучение, незначительно влияет на число фотонов в резонаторе, т. е. и на амплитуду поля.
Согласно рассмотренному выше, амплитуда электрического поля выходного пучка может быть записана как E(t) = E0sin[2nvLt + cpn(f)], где ср„(£) — случайная переменная, отвечающая за нулевые флуктуации поля. Далее можно показать, что зависимость величины ф„(£) от времени имеет общее с диффузионными процессами, т. е. среднеквадратичное отклонение фазы в момент времени t, или Лф(/) = ([фп(£) - фп(0)]2)1/2, пропорционально величине 4t. Спектр излучаемого света, т. е. спектр мощности E(t), имеет лоренцев контур, причем его ширина (на половине максимального значения) при пренебрежении внутренними потерями определяется выражением [23]:
N2 2nhvL(Avc)2
Где Р — выходная мощность. Данное выражение представляет собой известную формулу Шавлова-Таунса, которая была предложена ими в оригинальной работе [24] и которая устанавливает квантовый предел для ширины лазерной линии.
Как правило, ширина линии, описываемая выражением (7.9.2), является пренебрежимо малой по сравнению с прочими механизмами уширения в резонаторах (которые будут разбираться позднее), за исключением весьма важного случая, имеющего отношение к полупроводниковым лазерам. Причина этого исключения заключается в том, что, как будет показано в следующем примере, величина Дус для полупроводникового лазера оказывается на пять порядков величины больше, чем, например, для He-Ne лазера. Действительно, проведенные эксперименты с лазером на арсениде галлия (GaAs) показали, что реальная ширина линии приблизительно в 50-100 раз превышает расчетную величину, полученную из выражения (7.9.2). Это наблюдение было позднее объяснено в рамках новых эффектов и особенностей, свойственных полупроводниковым лазерам. Флуктуации плотности электронно-дырочных пар, вызванные спонтанными переходами, приводят к измеримым флуктуациям показателя преломления активной среды. В свою очередь, флуктуации длины резонатора приводят к изменению резонансной частоты и, следовательно, частоты генерации. Таким образом, при рассмотрении полупроводниковых лазеров необходимо в правой части выражения
(7.9.2) добавить множитель, который можно обозначить как а2 и который оказывается значительно больше единицы. Параметр а называется фактором Генри, в честь ученого, который первым объяснил этот эффект [25].
Пример 7.9. Пределы монохроматичности в Не-Ые лазере и в полупроводниковом СаАв лазере. Рассмотрим вначале одномодовый Не-Ке лазер, генерирующий на красном переходе (X = 632,8 нм, у0 = 4,7 • 1014 Гц). Пусть Ье= 1 м, у = 1%. Предположим также, что выходная мощность Р = 1 мВт. Из выражений (7.2.14) и (5.3.10) получаем соответственно тс = 3,3 • 10-7 с и ус = 4,7 • 105 Гц. Из соотношения (7.9.2), принимая ^2/(Л^2 - Nl) = 1, получаем = 0,43 мГц.
Теперь рассмотрим одномодовый полупроводниковый лазер на ОаАв (X = 850 нм) с резонатором длиной Ь = 1 = 300 мкм и коэффициентом отражения Я = 0,3 для выходных торцов резонатора (т. е. равным френе - левским потерям на поверхностях полупроводника без покрытия). Пренебрегая прочими потерями в резонаторе, находим у =-1п(Л) = 1,03 и, следовательно, тс = пЬ/су = 3,4 пс, где п = 3,5 — показатель преломления материала ОаАв. Далее получаем Аус = 1/2птс = 4,7 • 1010 Гц, и из выражения (7.9.2), полагая АГ2/(АГ2 - Мг) = 3 и Р = 3 мВт, находим Ау1 = 3,2 МГц. Следует отметить, что ширина лазерной линии в этом случае почти на 10 порядков величины больше, чем для Не-Ке лазера, вследствие значительно более короткого времени перехода и, следовательно, значительно большей ширины линии резонатора.
Исходя из рассмотренного примера ширина линии полупроводникового лазера определяется квантовым шумом и на практике ее трудно уменьшить до значений ниже 1 МГц. Для He-Ne лазера, а также для всех других лазеров (например, Nd: YAG, С02 или Ar лазеров) ширина линии определяется формулой Шавлова-Таунса, и для маломощных милливаттных лазеров может составлять порядка 1 Гц и ниже и может быть даже уменьшена до значений мГц. Так, для He-Ne лазера (vL = с/Х = 4,7 • 1014 Гц) относительная монохроматичность, обусловленная нулевыми флуктуациями поля, составила бы (Avl/vl) = 2,7 - 10~18.
Рассмотрим теперь, какие требования следует предъявить к стабильности длины резонатора, чтобы стабильность резонансной частоты поддерживалась с указанной выше точностью. Из выражения (5.1.2), принимая п = const, находим (AL/L) = —(Avc/vc) = 2,7 • 10~18, таким образом, при!, = 1 м имеем AL £ 2,7 • 10"9 нм. Это означает, что изменения длины резонатора на величину, которая в ~108 раз меньше типичного размера атома, уже достаточно для того, чтобы вызвать сдвиг резонансной частоты vc и, следовательно, частоты генерации vL, которая сравнима с шириной линии генерации, определяемой выражением (7.9.2). Таким образом, на практике предельная монохроматичность излучения определяется изменениями длины резонатора, обусловленными вибрациями или тепловыми эффектами, как будет видно в следующем разделе. Эти изменения обусловлены различными механизмами, которые, возможно, имеют несколько иную природу, чем это было описано выше, и относятся к так называемым техническим шумам.