КВАЗИТЕХУРОВНЕВЫЙ ЛАЗЕР
В квазитрехуровневом лазере нижний лазерный уровень (уровень 1 на рис. 7.2) является подуровнем основного состояния, и предполагается, что все подуровни основного состояния являются сильносвязанными и, следовательно, находятся в тепловом равновесии. Подобным образом верхний лазерный уровень 2 может являться подуровнем верхнего состояния, где все подуровни, как предполагается, также находятся в тепловом равновесии. В этом случае обозначим через и А^2 населенность основного состояния и населенность всех подуровней верхнего состояния соответственно. Предположим опять, что
|
Рис. 7.2 Схема квазитрехуровневого лазера |
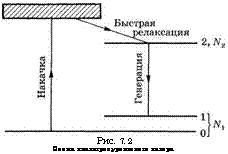 Релаксация с уровня (или уровней) накачки на подуровни верхнего состояния осуществляется очень быстро, и, таким образом, мы имеем дело только с населенностями АГ1 и Ы2 (идеальная квазитрехуровневая схема). Теперь обозначим уровень 0 как низший подуровень основного состояния и предположим, что разница в энергиях между подуровнями 1 и 0 сравнима с величиной кТ. Тогда нижний лазерный уровень будет иметь некоторую долю населенности основного состояния (см. раздел 2.7.2); что явля
Релаксация с уровня (или уровней) накачки на подуровни верхнего состояния осуществляется очень быстро, и, таким образом, мы имеем дело только с населенностями АГ1 и Ы2 (идеальная квазитрехуровневая схема). Теперь обозначим уровень 0 как низший подуровень основного состояния и предположим, что разница в энергиях между подуровнями 1 и 0 сравнима с величиной кТ. Тогда нижний лазерный уровень будет иметь некоторую долю населенности основного состояния (см. раздел 2.7.2); что явля
Ется результатом поглощения генерируемых фотонов.
Следуя рассуждениям раздела 2.7.2, запишем скоростные уравнения для подуровней верхнего и нижнего лазерного состояний, используя обозначения для полных населенностей и При этом скоростные уравнения для квазитрехуровневого лазера можно записать почти так же, как и в случае четырехуровневого лазера, принимая во внимание тот факт, что теперь имеют место как поглощение, так и вынужденное излучение генерируемых фотонов. Таким образом, запишем:
#! + ЛГ2 = М, (7.2.19а)
Т2/(11) = Др - ф(ВеМ2 - ад) - (ЛГ2/Т), (7.2.196)
Щ/сН) = УМВ^2 - £алгх) - (ф/тД (7.2.19в)
Где х опять обозначает эффективное время жизни уровня 2, и величины Ве и Ва в данном случае описываются выражениями:
Ве = оес/У, (7.2.20а)
Ва = оас/У, (7.2.206)
Где ае и ста — эффективные сечения переходов для вынужденного излучения и поглощения соответственно (см. раздел 2.7.2). Далее, подставляя выражения (7.2.20) в уравнения (7.2.19), получаем:
Nl + N2 = Nt, (7.2.21а)
|
£[£_ СН У |
|
(АГ2-/^)-^ Ф. Хс_ |
|
К. |
![]() (7.2.22)
(7.2.22)
Из уравнений (7.2.216, в) можно теперь определить инверсию населенностей N как
N = N2-fNl. (7.2.23)
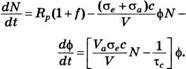
|
Х |
![]() Используя уравнение (7.2.21а) и выражение (7.2.23), можно выразить Ыг и Ы2 через значения N и Л^. Уравнения (7.2.21) можно затем преобразовать в два уравнения для переменных ф и N. После некоторых несложных преобразований получаем:
Используя уравнение (7.2.21а) и выражение (7.2.23), можно выразить Ыг и Ы2 через значения N и Л^. Уравнения (7.2.21) можно затем преобразовать в два уравнения для переменных ф и N. После некоторых несложных преобразований получаем:
(7.2.24а)
(7.2.246)
В рамках ограничений, введенных для уравнений (7.2.16), уравнения
(7.2.24) описывают статический и динамический режимы работы квазитре-
Хуровневого лазера.[30] В случае переходного режима работы лазера, если накачка начинается с момента времени £ = 0, уравнения (7.2.24) должны решаться с начальными условиями N(0) = - fN1 и ф(0) = ф7 « 1. Необходимо отметить, что скоростные уравнения (7.2.166) для четырехуровневого и (7.2.246) для квазитрехуровневого лазера имеют одинаковый вид, тогда как скоростные уравнения для инверсии населенности несколько отличаются. В частности, величина (ае + ста)/ае, описывающая вынужденное излучение, оказывается больше, чем для четырехуровневого лазера. Для объяснения этого факта рассмотрим единичный объем Уд = 1 и предположим, что в этом объеме за промежуток времени Л£ в результате вынужденного процесса рождается один фотон. Согласно уравнению (7.2.246) это подразумевает, что (аесЛГф/У)А£ = 1. Учитывая этот результат, из уравнения (7.2.24а) можно видеть, что инверсия N уменьшается на величину ДАТ = [(ае + <Ja)cNty/V]At = (+ оа)/ое. Запись АN > 1 подразумевает, что вследствие вынужденных процессов величина И2 уменьшается на единицу, тогда как N1 увеличивается на единицу. Согласно выражению (7.2.23), уменьшение значения N должно быть, на самом деле, больше, чем на единицу. С другой стороны, для четырехуровневого лазера при излучении одного фотона населенность ЛГ2 уменьшается на единицу, тогда как населенность остается практически неизменной (т. е. равной нулю,
Благодаря быстрой релаксации 1 -> 0). Таким образом, в данном случае инверсия N становится равной единице. Необходимо также отметить, что в случае, когда значения са и, следовательно, f стремятся к нулю, уравнения
(7.2.24) сводятся к уравнениям (7.2.16).
Таким образом, в рамках модели пространственно-независимых скоростных уравнений, уравнения (7.2.24) представляют собой конечный результат вычислений для схемы квазитрехуровневого лазера. Для обоих случаев, как для непрерывного, так и для динамического режимов работы лазера, решение этих уравнений с соответствующими граничными условиями позволяют определить параметры N и ф; при этом выходную мощность излучения, например на выходе зеркала 2, можно получить из выражения (7.2.18).