ПОПЕРЕЧНОЕ СЕЧЕНИЕ ВОЗБУЖДЕНИЯ ЭЛЕКТРОННЫМ УДАРОМ
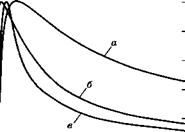
На рис. 6.22 показана качественная зависимость сечений возбуждения электронным ударом ст от энергии налетающих электронов Е для трех случаев: (1) разрешенных оптических переходов, (2) запрещенных оптических переходов без изменения мультиплетности, (3) запрещенных оптических переходов с изменением мультиплетности. Для всех трех случаев максимальная величина а нормирована на единицу. Отметим, что для каждого из случаев существует определенная пороговая энергия Егк, при превышении которой сечения становятся отличными от нуля. Как можно было бы ожидать, величина Еоказывается близкой к разности энергий уровней, связанных рассматриваемым переходом. Сечения резко возрастают при превышении пороговой энергии, достигают максимальной величины, а затем медленно уменьшаются. Максимальная величина а и ширина соответствующей кривой зависят от типа перехода:
■ для разрешенных оптических переходов максимальная величина а обычно достигает 10~16 см2, а характерная ширина кривой может быть в 10 раз больше, чем пороговая энергия (кривая а на рис. 6.22);
■ для запрещенных оптических переходов без изменения мультиплетности максимальная величина сг почти на три порядка меньше (до 10~19 см2),
|
0 2 4 6 8 10 12 E/E, h |
|
0 |
|
« G0,8 |
|
Ф |
|
И 0,6 |
|
И |
|
|
|
|
|
|
|
![]()
Гается, что взаимодействие настолько слабое, что вероятность одного перехода атома за время удара очень мала, а двух таких переходов не происходит вообще. В этом случае уравнение Шредингера для рассматриваемой задачи можно линеаризовать. Кроме того, оказывается, что сечение перехода можно выразить в виде:
|
(6.4.8) |
![]() Пе ос| |[ц2 ехр(/к„ • r)]»[Ul ехрО'ко • Г)]dV |2 .
Пе ос| |[ц2 ехр(/к„ • r)]»[Ul ехрО'ко • Г)]dV |2 .
Из приведенного выражения для длины волны де Бройля, предполагая, что энергия электрона составляет всего несколько эВ, видим, что величина параметра X' = 2я/|к0 - kJ = 2л/|Ак| существенно превышает размеры атома (-0,1 нм). Это означает, что (Дк • г) <С 1 при |г| ^ а, где а — радиус атома. В этом случае множитель ехр Д(к0 - кд) • г] = ехр ДА к • г) в (6.4.8) можно разложить в ряд по малому параметру (Ак • г). Поскольку функции иг и и2 ортогональны, то первый член в этом разложении, который дает отличный от нуля вклад в ое, равен ;(Ак • г), откуда получаем:
|
|
(6.4.9)
Где |и21 — матричный элемент электрического дипольного момента атома (см. (2.3.7)). Отсюда следует, что при х21 * 0, т. е. когда переход является разрешенным оптическим, сечение возбуждения перехода электронным ударом пропорционально сечению поглощения фотона для этого перехода. Таким образом, следует ожидать, что сильные разрешенные оптические переходы будут иметь также большое сечение возбуждения электронным ударом. Для запрещенных оптических переходов без изменения мультиплетности (с АЗ = 0, например, для перехода 1х5 -» 2в Не; см. главу 10) интеграл (6.4.8) имеет ненулевое значение только для следующего, более высокого порядка, члена в разложении ехр;(Ак • г), а именно -(Ак • г)2/2. При этом выражение для ое может теперь быть записано в виде
|
|
Это выражение полностью отличается от того, которое соответствовало бы взаимодействию с фотоном, т. е. магнитному дипольному взаимодействию. Поэтому не удивительно, что отношение максимальных значений сечений электронного возбуждения для запрещенного и разрешенного переходов Gforbidden/°allowed равно в данном случае примерно 10-3, тогда как было показано ранее, аналогичное отношение сечений поглощения составляет ~10“5 (см. (2.4.14)). Таким образом, запрещенные оптические переходы относительно легче возбуждаются при столкновении с электроном, чем при «столкновении» с фотоном (поглощении). Данное обстоятельство имеет большое значение с точки зрения принципов работы газовых лазеров, поскольку накачка в них зачастую осуществляется через запрещенные оптические переходы.
Если мультиплетность при переходе изменяется (например, при переходе VS —> 2sS в Не; см. главу 10), то в борновском приближении вклад в сечение любого из членов разложения ехр ДАк • г) равен нулю. Действительно, такой переход предполагает изменение спина, тогда как в приближении
Борна налетающий электрон, в результате электростатического взаимодействия, может влиять только на орбитальное движение электронов атома, но не на их спин.1 Теоретическое описание данного случая, основанное на работах Вигнера, исходит из предположения, что при столкновении должен сохраняться суммарный спин атома и налетающего Электрона, но не обязательно спин одного только атома. Таким образом, переходы могут происходить за счет столкновений с обменом электронов, когда налетающий электрон замещает участвующий в переходе электрон в атоме, а последний, в свою очередь, испускается атомом. Для того чтобы сохранялся полный спин системы, спины налетающего и испущенного электронов должны быть направлены противоположно.
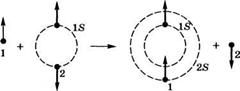
Для пояснения рассматриваемого процесса обмена на рис. 6.23 показано возбуждение электронным ударом перехода —» 2в Не. Отметим,
Что это столкновение можно представить следующим образом: налетающий электрон, обозначенный как 1, захватывается в состояние атома Не,
|
1 Это предполагает слабость спин-орбитального взаимодействия, которая характерна для легких атомов (например, Не, №), но не наблюдается в тяжелых атомах, таких как Нй. |
![]() Тогда как электрон атома, имеющий противоположный спин и обозначенный как 2, испускается. Однако приведенное описание является достаточно примитивным, поскольку непосредственно во время столкновения два электрона являются квантовомеханически неразличимыми (т. е. фактически при столкновении происходит спиновый обмен, а не обмен электро - ] нов). Тем не менее, из этого простого описания нетрудно видеть, что такой обменный механизм должен быть более резонансным, чем тот, который^ был рассмотрен в борновском приближении. Действительно, вероятность! того, что переход с обменом электрона произойдет, будет велика только в| тех случаях, когда энергия налетающего электрона близка разности энер-1 гий связанных переходом состояний. Фактически в этом случае энергии на - ] летающего электрона как раз хватает для того, чтобы после столкновения! электрон 1 остался*в возбужденном состоянии 2§, в то время как электрон 2 ] испустился с нулевой скоростью. При более высоких энергиях налетающего| электрона в результате процесса обмена электрон 1 остается в состоянии 2«, | а испущенный атомом электрон 2 должен унести соответствующую избы-| точную энергию. Такая ситуация определенно будет менее вероятна. Уста-| новив, что рассмотренный процесс спинового обмена является в некотором! смысле резонансным, можно понять, почему пиковое значение его сечения ] может оказаться выше, чем сечения запрещенного оптического перехода! без изменения спина. ]
Тогда как электрон атома, имеющий противоположный спин и обозначенный как 2, испускается. Однако приведенное описание является достаточно примитивным, поскольку непосредственно во время столкновения два электрона являются квантовомеханически неразличимыми (т. е. фактически при столкновении происходит спиновый обмен, а не обмен электро - ] нов). Тем не менее, из этого простого описания нетрудно видеть, что такой обменный механизм должен быть более резонансным, чем тот, который^ был рассмотрен в борновском приближении. Действительно, вероятность! того, что переход с обменом электрона произойдет, будет велика только в| тех случаях, когда энергия налетающего электрона близка разности энер-1 гий связанных переходом состояний. Фактически в этом случае энергии на - ] летающего электрона как раз хватает для того, чтобы после столкновения! электрон 1 остался*в возбужденном состоянии 2§, в то время как электрон 2 ] испустился с нулевой скоростью. При более высоких энергиях налетающего| электрона в результате процесса обмена электрон 1 остается в состоянии 2«, | а испущенный атомом электрон 2 должен унести соответствующую избы-| точную энергию. Такая ситуация определенно будет менее вероятна. Уста-| новив, что рассмотренный процесс спинового обмена является в некотором! смысле резонансным, можно понять, почему пиковое значение его сечения ] может оказаться выше, чем сечения запрещенного оптического перехода! без изменения спина. ]
|
|
|
Рис. 6.23 Спиновый обмен при переходе І1^ —► 235 в атоме Не |
|
Не[11в] |
|
Не [23в] |