ПОРОГОВАЯ МОЩНОСТЬ НАКАЧКИ ДЛЯ ЧЕТЫРЕХУРОВНЕГО И КВАЗИТРЕХУРОВНЕВОГО ЛАЗЕРОВ
Применяя результаты расчетов эффективной скорости накачки, полученные в разделе 6.3.3, можно найти ожидаемую пороговую скорость накачки и пороговую мощность накачки для данного лазера. Рассмотрим два важных случая:
■ идеальный четырехуровневый лазер, в котором атомы после накачки мгновенно переходят на верхний лазерный уровень, а нижний лазерный уровень не заселен (см. рис. 1.4б);
■ идеальный квазитрехуровневый лазер, в котором атомы после накачки также мгновенно переходят на верхний лазерный уровень, а нижний лазерный уровень является подуровнем основного уровня.
К первому случаю относятся лазеры на таких активных средах, как Nd: YAG при X = 1,06 мкм или X = 1,32 мкм, Ti:Al203 и Cr:LISAF или LICAF. В наиболее важных лазерах, относящихся ко второму случаю, используются такие активные среды, как Nd:YAG при X = 0,946 мкм, Ег:стекло или УЬ:Ег:стекло при X = 1,45 мкм, Yb:YAG или УЬ:стекло и Tm:Ho:YAG.
Рассмотрим вначале идеальный четырехуровневый лазер и предположим, что верхний лазерный уровень в действительности состоит из множества сильно связанных подуровней, с суммарной населенностью N2. В соответствии с соотношением (1.2.5) пороговую величину N2c можно выразить в виде N2с = у/<5е1, где через се обозначено эффективное поперечное сечение вынужденного излучения (см. раздел 2.7.2). В действительности, это выражение справедливо только в пространственно-однородной модели, т. е. когда как Rpy так и конфигурация моды и2 считаются не зависящими от пространственных координат. Если принять во внимание пространственные зависимости, то предыдущее выражение для пороговой населенности верхнего уровня изменяется следующим образом (см. Приложение Д):
|
(6.3.16) |
|
N а J а |
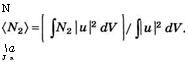 Где (N2) — эффективная величина населенности, определяемая как
Где (N2) — эффективная величина населенности, определяемая как
(6.3.17)
|
(6.3.18) |
|
Критическая, или пороговая, скорость накачки может теперь быть определена из условия, что скорость накачки атомов на верхний уровень должна равняться скорости спонтанного излучения возбужденными атомами. Отсюда получаем Щ = N2с/т9 где т — эффективное время жизни верхнего лазерного уровня, связанное с переходами со всех подуровней (см. раздел 2.7.2). Сле- |
|
(Rp) = {N2)c/t. |
|
Довательно, |
 |
|
|
|
|
![]()
Определив пороговое значение скорости накачки, можно легко найти соответствующую пороговую мощность накачки. Подставляя (6.3.19) в (6.3.12) и (6.3.14), получаем следующие выражения:
|
Na* |
|
T J<5e[l-exv-(2a2/w*)]y |
|
Hvn |
|
|
|
|
|
|
|
|
|
|
Которые относятся соответственно к случаям продольной и поперечной накачки. Выражение для пороговой мощности продольной накачки (6.3.20) согласуется с формулой, впервые полученной в [8]. Отметим, что при продольной накачке пороговая мощность возрастает по мере увеличения w0, поскольку при этом периферийная часть моды расширяется в менее накачанные области активной среды. При поперечной накачке в модели стержня с оболочкой пороговая мощность также возрастает по мере увеличения w0, поскольку при этом периферийная часть моды расширяется в область оболочки, т. е. в ненакачанную часть среды. Аналогичные соображения справедливы и для более близкого к реальности случая — стержня без оболочки. Однако в этой ситуации расчеты оказываются более сложными, поскольку, вообще говоря, соотношение (6.3.9) уже не применимо и следует использовать реальное пространственное распределение напряженности электрического поля, определяемое апертурными эффектами за счет конечного диаметра стержня. Однако если w0 оказывается заметно меньше, чем а (например, w0 < 0,7а), то наличие такой апертуры не существенно влияет на распределение напряженности и можно считать, что соотношение (6.3.21) справедливо и для стержня без оболочки. Конечно, в этом случае член [1 - ехр -(2а2/ьи$)] практически равен 1, так что при расчетах пороговой мощности накачки этот множитель в (6.3.21) может быть даже опущен. Однако, как будет показано в главе 7, важно сохранять этот член в (6.3.21) для корректного расчета величины дифференциального КПД.
Для сравнений, которые будут проводиться в разделе 6.3.5, необходимо также рассчитать пороговую мощность ламповой накачки. Из (6.3.15) и
(6.3.19) имеем:
|
Ae[l-exp-(2 a2/wg)] |
|
Па“ |
|
У ЦР1 |
|
Pth = |
|
||
|
||
Рассмотрим теперь квазитрехуровневый лазер, у которого нижний лазерный уровень является подуровнем основного уровня (уровня 1), и будем считать, что частицы, возбужденные в процессе накачки, мгновенно переходят на верхний лазерный уровень (идеальный квазитрехуровневый лазер). Предположим, что все подуровни основного уровня являются сильно связанными и, следовательно, находятся в тепловом равновесии, и пусть ЛГ] обозначает полную населенность уровня 1. Предположим также, что верхний лазерный уровень (уровень 2) состоит из нескольких сильно связанных подуровней, и пусть N2 — полная населенность уровня 2. Пороговые значения
Для населенностей этих двух уровней снова определяются из условия, что полное усиление равно потерям. Тогда с учетом пространственных зависимостей и в соответствии с соотношением (6.3.16) получаем (см. Приложение Д):
|
(6.3.23) |
Где через (Ы2) и (N1) снова, как и в (6.3.17), обозначены пространственно усредненные величины, а ое и ои — соответственно эффективные поперечные сечения вынужденного излучения и поглощения. Поскольку для идеального квазитрехуровневого лазераf N2 = Л^, то (Л^) + (ЛГ2) = Л/^, и, подставив это соотношение в (6.3.23), можно легко найти (ЛГ2>г - Эффективная величина пороговой скорости накачки по-прежнему должна удовлетворять соотношению (6.3.18). Используя полученную описанным способом величи-
|
(6.3.24) |
![]() Ну (ІУ2)С, имеем:
Ну (ІУ2)С, имеем:
|
|
Отметим, что (6.3.24) очевидным образом преобразуется в (6.3.19), если положить оа —> 0.
![]() При расчете соответствующей пороговой мощности накачки ограничимся рассмотрением случая продольной накачки, поскольку это единственная конфигурация, позволившая получить лазерную генерацию при достаточно низком пороге. Из (6.3.24) и (6.3.12) получаем:
При расчете соответствующей пороговой мощности накачки ограничимся рассмотрением случая продольной накачки, поскольку это единственная конфигурация, позволившая получить лазерную генерацию при достаточно низком пороге. Из (6.3.24) и (6.3.12) получаем:
(6.3.25)
Что согласуется с соотношением, впервые полученным Фэном и Байером [19]. Отметим, что (6.3.25) преобразуется в (6.3.20), если положить оа -» 0.