ПРИНЦИПЫ ЛАЗЕРОВ

СОБСТВЕННЫЕ ЗНАЧЕНИЯ

Сравнение соотношений (4.7.29) и (4.7.30) показывает, что если АВСБ- матрица является матрицей обхода резонатора и д = то распределение ам­

Плитуд напряженности электромагнитного поля и(х> у, 2Ь) после одного об­хода с точностью до амплитудного множителя 1 ДА + (Б/д)]1+/+т равна перво­начальному распределению и(хг = х, ух = у, гг = 0). Согласно (5.2.2) отсюда следует, что

СТгт=[А + (В/9)]1+г+т‘ (5.5.14)

Из (5.5.3) видно, что поскольку А = I), то имеем:

Д = 1^в7с. (5-5Л5>

Если теперь записать

А=А + (В/я), (5.5.16)

То из (5.5.16), используя (5.5.15), получаем |с|2 = А2 - ВС =АО — ВС = 1. То­гда из (5.5.14) следует, что величина а*т также равна 1 и, согласно (5.2.6), дифракционные потери уш равны нулю. Действительно, этого следовало бы

Ожидать в результате проведенного анализа, поскольку с самого начала ог варивалось, что предполагается отсутствие ограничивающих диафрагм (рис. 5.8г), и, в частности, рассматривался двухзеркальный резонатор с бес­конечно большими размерами зеркал (рис. 5.8в).

Для того чтобы получить выражение для фазы собственного значения а//п, запишем:

С = ехр - уф.

Из выражений (5.5.17) и (5.5.16), используя (5.5.15) и (5.5.5), имеем:

Віпф = В4-С/В = 2BlD1j-A1Cl/B1Dl.

Из (5.5.186) видно, что 0 < ф < тс при BXDX >0и-7і<ф<0 при BXDX < 0. Из (5.5.18а)получаемсов2(ф/2) = (1 + созф)/2 =A1D1 и, следовательно,

Ф = 2 arccos(±V^iA )>

Где положительный или отрицательный знак выбирается в зависимости от того, положительна или отрицательна величина ВiD^ Из соотношений (5.5.14), (5.5.16) и (5.5.17) получаем a/m = exp у( 1 +1 + т)ф = ехруф/т, т. е. ф/т = (1+1 + т)ф. Тогда из (5.5.19) и (5.2.7) имеем:

При этом знак «+» или «—» снова определяется тем, положительной или от­рицательной является величина В11)1.

В частном случае двухзеркального резонатора матричные элементы Аг и можно получить из (5.5.7). При этом соотношение (5.5.20) преобразуется в

N + ~~l + ~ arccos( ± Vffig2) .

71

И в соответствии с (5.5.7) знак «+» или «-» выбирается в зависимости от того, положительна или отрицательна величина ё2 (и, следовательно, величина

Пример 5.6. Спектр частот конфокального резонатора. Для симмет­ричного конфокального резонатора (^ = ё2 = 0) из (5.5.21) имеем

Vlmn ~ ^ [2аі + (1 + I + ПІ)].

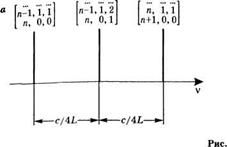
Соответствующий спектр частот показан на рис. 5.10а. Видно, что моды, ха­рактеризующиеся одними и теми же значениями суммы 2п + 1 + т, имеют одинаковую резонансную частоту, хотя их пространственные конфигурации и различны. Такие моды называют частотно-вырожденными. Расстояние по частоте между последовательными модами составляет при этом с/4Ь, а не с/2Ь9 как в плоскопараллельном резонаторе (см. соотношение (5.1.3)). Однако две такие последовательные моды должны иметь различные пары величин (/, т); таким образом, величина с/4Ь соответствует разности час­тот двух последовательных поперечных мод (например, (/г, 0, 0) —> (п, 0, 1)).

(га, 0,0)

/ Г(л, 1,0)(п,0,1)]

/ [(л, 1,1)(тг,0,2)]

/

- (c/2L)(2L/7i2Я)1/2

-c/2L-

Спектр частот симметричных (а) конфокального и (б) квазиплоского резонаторов

С другой стороны, расстояние по частоте между двумя модами с одинаковы­ми парами величин (/, т) (например, в моде ТЕМ00) и отличающимися на 1 по п (т. е. расстояние по частоте между соседними продольными модами) по - прежнему равно с/2Ь, так же как и в плоскопараллельном резонаторе.[25]

Пример 5.7. Спектр частот симметричного квазиплоского резонато­ра. В этом случае gx = g2 = 1 - (L/R), где L/R <С 1. Таким образом, величина g положительна и немного меньше 1. Соответственно arccos (g) = arccos [1 -

- (L/R)] = (2L/Rf'2, а (5.5.21) принимает вид

Соответствующий спектр частот показан на рис. 5.106. Видно, что расстоя­ние по частоте между соседними продольными модами снова равно с/2Ь, тогда как разность частот двух последовательных поперечных мод равна (<с/2Ь)(2Ь/п2Н)!/2.

5.5.1.3.

СТОЯЧИЕ И БЕГУЩИЕ ВОЛНЫ В ДВУХЗЕРКАЛЬНОМ РЕЗОНАТОРЕ

Продолжая обсуждение вопросов о размерах пятен и резонансных часто­тах в обобщенных резонаторах, начатое в разделах 5.5.1.1-2, перейдем те­перь к описанию соответствующих изменений моды вдоль резонатора лазера. Ограничимся при этом рассмотрением случая двухзеркальных резонаторов.

Согласно соотношениям (4.7.31) и (4.6.4), напряженность электрическогр поля в резонаторе может быть представлена в виде:

Xexp [-jkz + j(l + l + m)$]x хехр [-jk(x2 + г/2)/2Я],

Где w(z), R(z) и ф(-г) определяются соотношением (4.7.17). Эти величины мо­гут быть найдены, если известны положение перетяжки и соответствующий размер пятна и>0. Отметим, что здесь явно показана зависимость собственной моды Й от трех индексов /, тип. Индексы I и т связаны с порядком поли­номов Эрмита в соотношении (5.5.24а). Индекс п также указан явно, посколь­ку к = 2nv/c, а резонансная частота также зависит от трех индексов I, тип (см. (5.5.21)). Эти индексы показывают следующее:

■ индексы I и т, как уже указывалось в разделе 4.7.4, определяют число нулей в распределениях напряженности поля соответственно вдоль осей хиу;

■ в соответствии с рассмотрением в разделе 5.1.1 индекс п определяет чис­ло полуволн стоячей волны вдоль резонатора, т. е. дает число нулей на­пряженности ПОЛЯ ВДОЛЬ ОСИ Z.

В заключение данного раздела рассмотрим вопрос о том, какую же волну описывает соотношение (5.5.24) для собственной моды поля: бегущую или стоячую. Ответ зависит от вида временной эволюции моды. Если записать, в соответствии с (4.6.1), Е = - Еехр(у'со£), где со = соimn = 2nvlmn — угловая частота моды, то продольный фазовый множитель в (5.5.246), например для моды ТЕМ00, будет иметь вид Е ос exp j[~kz + ф + со£], что соответствует волне, рас­пространяющейся в положительном направлении оси z, Если, с другой сто­роны, записать Е = 2£ехр(-усо£), то получим волну, распространяющуюся в отрицательном направлении оси z. Собственная мода в виде стоячей волны получается как сумма этих двух волн, т. е. при записи EccЙcoswt. Следуя этому рассуждению, видим, что с точностью до множителя, определяемого коэффициентом пропускания зеркала, Е = Лexp(j(щt) представляет собой так­же волну, выходящую из резонатора через зеркало 2 и распространяющуюся в положительном направлении оси г.