РЕЗОНАТОРЫ С БЕСКОНЕЧНО БОЛЬШОЙ АПЕРТУРОЙ
Обращаясь к рис. 5.66 для обобщенного резонатора и рис. 5.5а для двухзеркального, предположим, что их апертуры бесконечно велики, т. е. положим, что ах = а2 = оо на рис. 5.5а. Распределение напряженности поля и(х, у, г) после одного обхода резонатора на рис. 5.5а (или прохода одного периода системы линз на рис. 5.56), т. е. при г = 2Ь, может быть получено из соотношения (4.6.9) при гх = 0, где в качестве АВС£)-матрицы взята матрица одного обхода (или прохода одного периода). Если в плоскости гх = О положить теперь Ё(хг ,У1,0) = и(хг, уг, 0), то в приближении параксиальных волн и в соответствии с (4.6.5) можно записать Ё(х, у, 2Ь) = и(х, у, 2Ь) ехр(-2]кЬ). Подставляя в это соотношение выражение для и(х, у, г), задаваемое (4.6.9), получаем:
|
ХЁ(х1,у1,0)ёх1ёу1. |
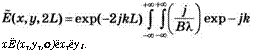 +уї) + Р(х2 + у2)-2х1х-2уіу~
+уї) + Р(х2 + у2)-2х1х-2уіу~
2 В ]
(5.5.1)
Сравнение соотношений (5.5.1) и (5.2.1) показывает, что функция распространения К(х, у;хг, уг) имеет в этом случае вид:
![]() А(х% + у2) + И(х2 +у2) — 2х1х — 2у1у~ (5.5.1а)
А(х% + у2) + И(х2 +у2) — 2х1х — 2у1у~ (5.5.1а)
1В
|
В 2ш0,= = 2юх |
|
2и>„ Л. |
|
Л-л. |
 |
|
|
|
|
|
|
|
|
|
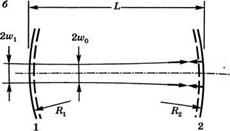
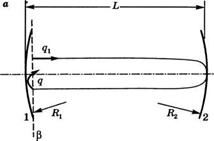
Рис. 5.8
А) Расчет д-параметра для двухзеркального резонатора, б) Размер пятна и поверхности равной фазы в двухзеркальном резонаторе, в) Преобразование двухзеркального резонатора в резонатор с плоскими зеркалами на выходе. г) Общее решение для случая плоских зеркал на выходе
Как объяснялось в разделе 4.7, гауссово решение низшего порядка — выражение (4.7.1), и общее решение более высокого порядка— выражение (4.7.30), являются собственными решениями уравнения распространения
(4.6.9) , когда в оптической системе, описываемой АВС2)-матрицей, нет ограничивающей диафрагмы. Для того чтобы эти собственные решения Эрмита - Гаусса соответствовали распределениям напряженности электрического поля в модах резонатора, требуется воспроизводимость пучка после одного обхода. Это значит, что если обозначить через комплексный параметр гауссова пучка, покидающего плоскость (3 перед, например, зеркалом 1 на рис. 5.8а, то комплексный параметр пучка д после одного обхода резонатора должен снова быть равен Из закона АВСБ для распространения гауссовых пучков, т. е. соотношения (4.7.4), положив = <?, получим равенство
Д = (5.5.2)
Это условие означает, что величина д должна удовлетворять квадратному уравнению
Сф + (X) - А)д - В = 0. (5.5.3)
Для того чтобы величина д была комплексной, необходимо и достаточно, чтобы дискриминант уравнения (5.5.3) был отрицательным, т. е. выполнялось условие
(Р —А)2 + 4ВС < 0. (5.5.4)
Однако, поскольку А1> - ВС = 1, условие (5.5.4) преобразуется к виду | (2) + А)2 < 4, т. е. является аналогичным условию (5.4.6). Это означает, что решения в виде гауссовых пучков существуют только в устойчивых резонаторах, или, другими словами, что все устойчивые резонаторы с бесконечно большой апертурой имеют моды, которые описываются общими решениями Эрмита-Гаусса вида (4.7.30).