ПЛОСКОПАРАЛЛЕЛЬНЫЙ РЕЗОНАТОР (ИЛИ РЕЗОНАТОР ФАБРИ-ПЕРО)
Плоскопараллельный резонатор {резонатор Фабри-Перо) состоит из двух плоских зеркал, расположенных параллельно друг другу. В первом приближении моды такого резонатора можно представить в виде суперпозиции двух плоских электромагнитных волн, распространяющихся в противоположных направлениях вдоль оси резонатора, как схематически показано на рис. 5.1а. В рамках этого приближения нетрудно определить резонансные частоты, если наложить условие, что длина резонатора Ь должна равняться целому числу полуволн, т. е. Ь = п(к/2)9 где п — положительное целое число. Такое условие необходимо для того, чтобы на поверхности обоих зеркал напряженность электрического поля стоячей электромагнитной волны была равна нулю. Отсюда следует, что резонансные частоты в этом случае определяются соотношением
У = п(с/2Ь). (5.1.2)
Отметим, что такое же соотношение можно получить, если наложить условие, что изменение фазы плоской волны после полного прохода резонатора (в прямом и обратном направлениях) должно быть кратно величине 2тг, т. е. должно выполняться равенство 2кЬ = 2пп. Это условие нетрудно получить из соображений самосогласованности. Если частота плоской волны равна
|
*------------ ь------------ ►! |
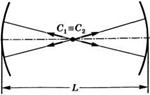
Рис. 5.1
А) Плоскопараллельный резонатор, б) Концентрический резонатор
Частоте моды резонатора, то набег фазы после одного полного прохода, или обхода, резонатора должен быть равен нулю (с точностью до целого числа величин 2я). Только в этом случае амплитуды последовательно отраженных волн в любой произвольной точке пространства будут складываться в фазе, давая значительную величину суммарной напряженности поля.
В соответствии с (5.1.2) разность частот двух последовательных мод, т. е. мод, для которых величины п отличаются на единицу, дается соотношением
Ау = с/2Ь. (5.1.3)
Эту величину называют разностью частот соседних продольных мод; название «продольная» используют потому, что число п равно числу полуволн моды вдоль оси резонатора лазера, т. е. в продольном направлении.
