КВАНТОВЫЕ НИТИ И КВАНТОВЫЕ ТОЧКИ
Из раздела 3.3 видно, что улучшение оптических характеристик, получаемое при переходе от объемного полупроводника к соответствующим полупроводниковым гетероструктурам с КЯ, связано в основном с проявлением квантового ограничения, обусловленного тем, что один из размеров изготавливаемой полупроводниковой структуры оказывается сравнимым с длиной волны де Бройля. Поэтому естественно расширить такой подход
|
Рис. 3.30 (а) Различные пространственные конфигурации и (б) соответствующие им виды зависимости плотности состояний от энергий электронов для объемного полупроводника и полупроводниковых структур с квантовыми ямами, квантовыми нитями и квантовыми точками (с разрешения, из [19]) |
![КВАНТОВЫЕ НИТИ И КВАНТОВЫЕ ТОЧКИ подпись: рис. 3.30 (а) различные пространственные конфигурации и (б) соответствующие им виды зависимости плотности состояний от энергий электронов для объемного полупроводника и полупроводниковых структур с квантовыми ямами, квантовыми нитями и квантовыми точками (с разрешения, из [19])](/img/655/image302.gif)
|
Квантовая Точка |
|
Ш Е‘ |
Е |
. Е, |
|
Шггг- |
||
|
3D -*► |
|
Объемный Полупроводник |
|
Кванті |
|
°вая |
|
Квантовая Нить |
|
104 |
![]()
|
2хНҐ |
![]()
|
-р J р ^a047^n053-^S/InP Г=зоок |
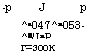
|
ЛГ = 3 х 1018 см-3 Точка [10 х 10 х 10 нм3] |
![]()
|
Нить [10 х 10 нм2] |
![]()
|
Яма [10 нм] |
![]()
|
Объемный полупроводник |
![]()
|
1,4 1,5 1,6 Длина волны, X [мкм] |
![]()
|
« К И О) Я >> Е-> И О) К ЕГ IS! •Є* F & |
![]()
|
/ |
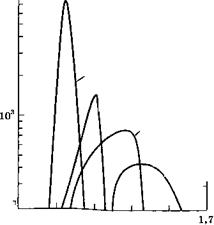
![]() Рис. 3.31 Расчетные зависимости коэффициента усиления от длины волны излучения при плотности инжектированных электронов N — 3 • 1018 см-3 для объемного полупроводника Оа0,471п0>51А8 и для квантовой ямы шириной 10 нм, квантовой нити с размерами 10 нм х 10 нм и квантовой точки с размерами 10 нм х 10 нм х 10 нм в Оа0>471п0 51Аз/1пР (с разрешения, из [19])
Рис. 3.31 Расчетные зависимости коэффициента усиления от длины волны излучения при плотности инжектированных электронов N — 3 • 1018 см-3 для объемного полупроводника Оа0,471п0>51А8 и для квантовой ямы шириной 10 нм, квантовой нити с размерами 10 нм х 10 нм и квантовой точки с размерами 10 нм х 10 нм х 10 нм в Оа0>471п0 51Аз/1пР (с разрешения, из [19])
И рассмотреть две других возможных структуры с квантовым ограничением, а именно квантовых нитей (англ. quantum wires) и квантовых точек (англ. quantum dots), которые изготавливаются таким образом, что два или все три их характерных размера становятся сравнимыми с длиной волны де Бройля (рис. 3.30а).
Как и в случае КЯ, принципиальная разница между этими квантово-ог - раниченными структурами и объемными соединениями обусловлена различным видом плотности состояний. Не входя здесь в детали (более подробное описание см. в [18]), приведем на рис. 3.306 качественный характер зависимости плотности состояний от энергий электронов для объемного полупроводника и для полупроводниковых структур с квантовыми ямами, квантовыми нитями и квантовыми точками. Используя эти разные виды плотности состояний, можно, применив тот же подход, что и в случае КЯ, рассчитать ожидаемый коэффициент усиления. Здесь этого делать не будем, а в качестве характерного примера ограничимся показом на рис. 3.31 зависимостей
А) Планарная линейка из квантовых нитей.
Б) Планарная матрица
Квантовая нить Квантовая точка из квантовых точек
Ожидаемого коэффициента усиления в веществе от длины волны излучения для структуры Оа0>471п0>51А8/1пР (Оа0 471п0>51А8 представляет здесь полупроводник с квантовым ограничением). На рисунке приведены значения коэффициента усиления в веществе для объемного полупроводника, для квантовой ямы шириной 10 нм, для квантовой нити с размерами 10 нм х 10 нм и для квантовой точки с размерами 10 нм х 10 нм х 10 нм — при одной и той же концентрации инжектированных электронов (ТУ = 3 • 1018см_3) [19]. Расчетные концентрации прозрачности для объемного полупроводника, квантовой ямы и квантовой нити примерно одинаковы (А^г = 1,3 • 1018 см-3), тогда как для квантовой точки эта концентрация немного выше (Л^г = 1,8 • 1018 см-3). В соответствии с обсуждавшимися ранее свойствами структур с квантовыми ямами, видно, что при переходе от объемного полупроводника к квантовой яме, от квантовой ямы к квантовой нити и от квантовой нити к квантовой точке коэффициент усиления возрастает. Ширина полосы усиления при тех же переходах от структуры к структуре, наоборот, уменьшается.
В качестве активных сред лазеров структуры с квантовыми нитями и квантовыми точками будут, по-видимому, использоваться в виде планарных линеек и матриц — типа тех, что изображены на рис. 3.32а и 3.326. Значительные технологические проблемы (связанные с необходимостью обеспечить высокую плотность упаковки, низкий уровень размерных флуктуаций и низкий уровень плотности дефектов) пока еще затрудняют массовое производство структур на основе квантовых нитей и квантовых точек с хорошими оптическими характеристиками. Если эти трудности будут преодолены, то появятся полупроводниковые лазерные материалы с более низкими пороговыми характеристиками, значительно более высокими дифференциальными коэффициентами усиления и узкими ширинами полосы усиления.
В главе 3, по сравнению с предшествующей, посвященной простым атомарным системам, были рассмотрены более сложные случаи молекул и полупроводников, свойства которых обсуждались достаточно детально. Как показывает проведенное рассмотрение, понимание оптических свойств этих веществ требует достаточно подробного описания их физических свойств. Такое описание было ограничено здесь наиболее простыми аспектами. Однако с феноменологической точки зрения, как будет видно в главах 7 и 8, для предсказания поведения лазера необходимо знание только нескольких физических параметров, а именно:
■ длины волны перехода и ширины полосы усиления;
■сечения перехода или, для полупроводников, дифференциального коэффициента усиления и концентрации носителей при условии прозрачности;
■времени жизни в верхнем состоянии или, для полупроводников, постоянной времени электрон-дырочной рекомбинации.
По существу, это наиболее важные физические параметры среди тех, что обсуждались в предшествующей и настоящей главах.