СПОНТАННОЕ ИЗЛУЧЕНИЕ И ЕЗЫЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ
|
Рассмотрим вначале процессы спонтанного излучения и определим спектральную плотность скорости переходов 11у так, что #ус/у представляет собой число спонтанных излучательных переходов в единице объема за единицу времени, при которых свет испускается в интервале частот от у до у + й. Для того чтобы рассчитать Лу, возьмем вначале элементарное число переходов р7(у0)с? у0, частоты которых попадают в интервал от у0 до у0 + с? у0. Они дадут вклад сШу в спектральную плотность который выражается как |
|
Где А2і = А2і(уо) — вероятность спонтанных излучательных переходов между двумя состояниями, а #(у - у0) — форма контура линии перехода. Следует отметить, что величина р7(у0) умножена на фактор /с (Е2) [1 - (Е{)], поскольку спонтанные переходы, так же как и вынужденные, могут происходить |
|
Только между заполненными верхними и свободными нижними состояния* |
|
Ми. Полная спектральная плотность скорости переходов получается от - I Сюда интегрированием приведенного выражения по всем частотам перехл - ^ |
|
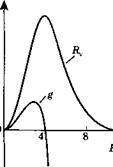
Качественный вид спектра спонтанного излучения Д, и коэффициента усиления # при определенной величине |
|
Рис. 3.20 |
|
Концентрации Инжектированных носителей (с разрешения, из [11]) |
 |
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
![]()
После того как определена спектральная плотность скорости спонтанных излучательных переходов Яу путем ее интегрирования по всем частотам излучения можно получить полную скорость Я. Таким образом,
Д= /А21/с(£Ш1-/Д£0]Р;М<*у. (3.2.45)
На практике, однако, часто используют феноменологическое соотношение
Я = BNeNh = ВЫ2, (3.2.46)
В котором В — характерная константа. Соотношение (3.2.46) может быть выведено, если предположить, что любой электрон может рекомбинировать с любой дыркой, откуда следует, что правила отбора по к строго не выполняются [9]. Не будем далее углубляться в обсуждение этого вопроса, который имеет отношение к так называемым краям зон в полупроводнике [Ю], и станем использовать (3.2.46) просто как феноменологическое соотношение, которое выполняется при рассматриваемых концентрациях электронов и дырок. Отметим, что из определения Я следует, что (с1Ке/&) = = - Я. Таким образом, можно ввести излучательное время жизни тг, полагая Я = А^/тг, и записать:
Рассмотрим теперь безызлучательные переходы. Они обычно происходят вблизи глубоких примесных центров, которыми захватывается носитель, электрон или дырка (рекомбинация в глубокой ловушке). Рассмотрим, например, полупроводник п-типа. При достаточно высоких степенях легирования уровень Ферми будет располагаться настолько близко к зоне проводимости, что эти центры будут удерживать электроны. В этом случае при рекомбинации свободной дырки со связанным электроном происходит безызлучательный переход, а избыточная энергия передается решетке. Аналогичное рассуждение справедливо при легировании р-типа. Для полупроводников с узкой запрещенной зоной безызлучательные переходы могут также происходить при непосредственной электрон-дырочной рекомбинации свободных электронов и дырок, при этом избыток энергии передается другому электрону (или дырке), которые возбуждаются в более высоколе - жащее состояние в зоне (рекомбинация Оже) [12]. Поскольку рекомбинация Оже — это трехчастичный процесс, то связанное с ним уменьшение плотности числа электронов может быть феноменологически описано уравнением (йКе/(И) = - СИеИу1Ме=-СЩ, где С— некоторая константа. При этом можно ввести безызлучательное время жизни за счет рекомбинации Оже тл, определяемое как
Для ОаАэ основным механизмом, которым обусловлены безызлучательные переходы, является, по-видимому, рекомбинация в глубоких ловушках, тогда как в полупроводниковых лазерных материалах длинноволнового диапазона, таких как ТпОаАэР, — рекомбинация Оже.
Пример 3.8. Излучателъные и безызлучательные времена жизни в (7аАв и 1пСаАзР. Для ОаАв положим В = 1,8 • Ю-10 см3с-1 и = Л/,г = 1,2 • 1018 см-3. Получим при этом тг = 1/В7У, г = 4,6 не, которое следует сравнить с измеренной, при условии прозрачности, величиной полного времени жизни т = 3 нс(Т = 300 К). Поскольку тг1 = т"1 + тп*, где тпг — время жизни, связанное с безызлучательными переходами, то находим, что величина безызлуча - тельного времени жизни тпг в данном случае — за счет рекомбинации в глубоких ловушках — составляет порядка 9 не. Для 1пОаАзР при X = 1300 нм возьмем В = 2 • Ю~10 см3с-1, АГС = Л^г= 1 • 1018 см-3 и С = 3 • 10-29 см6с-1. Из (3.2.47) получим тг = 5 не, а из (3.2.48) — тА = 33,3 не, которые определяют полное время жизни т, хорошо согласующееся с измеренным значением т = 5 не (Т = 300 К).
Из материала данного раздела видно, что процессы, приводящие к излуча - тельным и безызлучательным переходам в объемных полупроводниках, являются значительно более сложными, чем аналогичные процессы в одиночных атомах или ионах, рассмотренные в главе 2. С практической точки зрения, однако, наиболее важными физическими параметрами, которые необходимы, чтобы предсказать характер работы лазера, являются дифференциальный коэффициент усиления, концентрация носителей при условии прозрачности Ntr и полное время жизни т для спонтанных переходов (обусловленное как излучательными, так и безызлучательными процессами). Для рассматриваемых здесь GaAs и растворов с InGaAs эти величины могут быть взяты из табл. 3.1. Следует напомнить, что время жизни т зависит от концентрации носителей, а величины, приведенные в этой таблице, соответствуют ее значению при условии равной прозрачности.
Подводя итог, напомним также, что соотношение (3.2.37) для коэффициента усиления относится к полупроводнику с большими размерами (объемному полупроводнику). В связи с этим величины коэффициентов усиления, приведенные в табл. 3.1, часто называют коэффициентом усиления для вещества (англ. material gain). В лазерах с двойными гетеропереходами реальные коэффициенты усиления меньше и определяются отношением поперечных размеров активного слоя и моды резонатора. Этот коэффициент усиления, часто называемый коэффициентом усиления для моды (англ. modal gain)9 зависит, таким образом, от конкретной конструкции лазера и будет рассмотрен в разделе главы 9, посвященном полупроводниковым лазерам.