ПОЛУКЛАССИЧЕСКИЙ ПОДХОД
Предположим, что некоторый атом, первоначально находившийся в возбужденном состоянии 2 с энергией Е2, переходит, со спонтанным излучением, в состояние 1 с энергией Ег (см. рис. 1. 1а). Полагая, что оба уровня являются невырожденными, запишем соответствующие волновые функции:
|/!(г, *) = м1(р)ехр[-/(Я1/Й)Ч (2.3.1а)
У2(г> О = Мг)ехр[-/СЕ2/ад, (2.3.16)
Где и12(г) — собственные функции двух стационарных состояний 1 и 2, г — радиус-вектор электрона, совершающего переход (начало координат совпадает с ядром), и Н = Ь/2 п. В процессе перехода 2 -» 1 атома его волновая функ - 1 ция может быть представлена в виде линейной комбинации волновых функ - 1 ций двух состояний:
V = МОУ] + а2(£)ц/2, (2.3.2)
Где аг и а2 — комплексные величины, зависящие от времени. Отметим, что согласно принципам квантовой механики |а^2 и а22 представляют собой вероятности того, что в момент времени t атом будет обнаружен соответственно в состоянии 1 или 2. Кроме того, опять же в соответствии с квантовомеханическим подходом, получаем: ]
М2 + |а2|2=1, (2.3.3)
Что подтверждает указанный выше смысл величин аг2 и а22.
Для описания того, как возникает спонтанное излучение, определим электрический дипольный момент атома |и. Согласно квантовомеханическому представлению имеем:
И = -|еМ2гОУ, (2.3.4)
Где е — заряд электрона; при этом интеграл берется по всему объему атома. Смысл выражения (2.3.4) можно легко понять, заметив, что e|ij/|2dF представляет собой элементарный заряд, который может быть обнаружен в объеме dV в точке г, и что данный заряд порождает элементарный дипольный
Момент dx = -(е | |/12 dV)г. Подставляя (2.3.2) в (2.3.4), с учетом выражений
(2.3.1) получим:
Ц= fer Iщ |2|u! I2 dV + era212|и2 |2 dV +
Г г п <2-3'5)
+ Jer[a, a5uiu2 exp j((o0t)+aa2ulu2 exp[-/((o0#)]JcfF,
Где знак * означает комплексное сопряжение, асо0 = (Е2 - Et)/h. Из выражения (2.3.5) видно, что ц содержит член ц08С, осциллирующий с частотой со0, который можно записать в виде:
Ц08С =Re[2a1a^21expy'(co0i)], (2.3.6)
Где через Re обозначена действительная часть числа. Здесь введен не зависящий от времени дипольный момент |л21, который определяется как
Ц21 = uieruydV. (2.3.7)
Вектор Ц21 называют матричным элементом оператора электрического диполь - ного момента, или электрическим диполъным моментом перехода атома.
Из выражения (2.3.6) видно, что в процессе перехода 2-^1 атом приобретает дополнительный дипольный момент [iosc, осциллирующий с частотой со0, амплитуда которого пропорциональна вектору ц21, определяемому выражением (2.3.7). Из классической термодинамики известно, что любой осциллирующий диполь излучает энергию в окружающее пространство. Таким образом, в рамках полу классического подхода спонтанное излучение может рассматриваться как результат такого испускания энергии. Для большей определенности запишем осциллирующий дипольный момент в виде:
Vosc = Ho cos(co0f + ф) = Re[no ехр(усо0*)]>
Где ц0 — вещественный вектор, описывающий амплитуду дипольного момента, Re обозначает действительную часть числа, а — комплексный век
Тор, определяемый как |Hq = |и0 ехр(у‘ф).[5] Согласно классической электродинамике такой осциллирующий диполь испускает в окружающее пространство излучение, мощность Рг которого определяется выражением:
П пх2 (щi
Р' =ОW' <2-3-8>
Где |1 =| |и0 1=1 |Ио | — амплитуда электрического дипольного момента, п — показатель преломления окружающей диполь среды, а с — скорость света в вакууме. Выражение (2.3.8) можно использовать и в рассматриваемом случае — при условии, что ц задается соотношением ц = 21 I» т-е - является
Амплитудой комплексного вектора 2ага2ц21• Таким образом, видно, что мощность излучения можно записать в виде:
Рг=Р;К|2|а2|2, (2.3.9)
Где Р/ — не зависящая от времени величина, задаваемая соотношением
16л3ге 1 ц |2 Ур (2.3.10)
Зе0с3 ’
В котором ||и| = |ц21| обозначает модуль комплексного вектора |и21-
Для того чтобы определить теперь вероятность, в единицу времени, перехода атома между данными состояниями со спонтанным излучением, или, кратко, спонтанного излучательного перехода, воспользуемся законом сохранения энергии и запишем:
~ = - Рг, (2.3.11)
Где энергия атома Е определяется как
Е = а12Е1 + а22Е2. (2.3.12)
Используя (2.3.3), соотношение (2.3.12) легко представить в виде:
Е=Ег + Ну0а22, (2.3.13)
Где у0 = (Е2 ~ Ех)/Н — частота перехода.
|
Й�2 |
![]() С помощью соотношений (2.3.9), (2.3.10) и (2.3.13) уравнение (2.3.11) можно переписать следующим образом:
С помощью соотношений (2.3.9), (2.3.10) и (2.3.13) уравнение (2.3.11) можно переписать следующим образом:
Р1«2 |2=—-41—К |2)|о2 I2, (2.3.14)
*яп
Где введено характерное время т8р = Ьу0 /Рг равное
3/18 0с3
(2.3.15)
8р 16я3у3п|Н2’
Которое называют временем жизни атома в состоянии (на уровне) 2 при спонтанном излучении, или излучашельным временем жизни атома в данном состоянии.[6] Решение уравнения (2.3.15) удобно представить в виде:
|
1 - 1апЬ |
|
2т*Р УJ |
|
|«2Н |
|
|
Где момент задается начальными условиями, а именно величиной |а2(0)|2. В самом деле, из (2.3.16) получаем соотношение
Откуда при заданном значении |а2(0)|2 (при условии, что оно меньше 1) можно однозначно определить /0. В качестве примера на рис. 2.5 показано изменение во времени величины |а2(*)|2 при начальном условии |а2(0)|2 = 0,96. Отметим, что выбор различных значений |а2(0)|2 фактически соответствует изменению величины £0 в (2.3.16), т. е. смещению начала оси времени. Если положить, например, |а2(0)|2 = 0,8, то кривую |а2(£)|2 можно получить про-
|
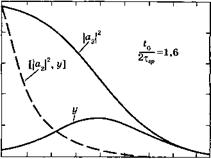
Стым горизонтальным сдвигом кривой на рис. 2.5 влево до тех пор, пока она не пересечет вертикальную ось £ = 0 в точке 0,8. В этом заключается преимущество представления временной эволюции величины |а2(£)|2 в виде (2.3.16). Определив |а2(£)|2, можно, используя (2.3.11) и (2.3.13), найти излучаемую мощность Рг, записав Рг = - /гу0<2|а2|2/<2£. Изменение во времени величины нормированной излучаемой мощности, у = х8рРг/Ну0, также представлено на рис. 2.5. Для последующего обсуждения важно заметить, что временную эволюцию величины |а2(£)|2 можно аппроксимировать экспоненциальной зависимостью вида:
М*)12 = М0)|2ехр [-(г/т, р)] (2.3.18)
Только при |а2(0)|2 <С 1. Действительно, произведя в этом случае замену |а!|2= 1 в уравнении (2.3.14), можно непосредственно получить соотношение (2.3.18).
Как будет более детально показано в следующем разделе, результаты, полученные с использованием полуклассического подхода, противоречат данным экспериментов. Корректные результаты можно получить, только применяя квантовый подход, при котором излучение также квантуется. Хотя такой расчет достаточно сложен и его особенности будут обсуждаться в следующем разделе, конечный результат оказывается простым и заключается в том, что соотношение (2.3.18) оказывается справедливым во всех случаях, при этом параметр х8р по-прежнему определяется формулой (2.3.15). Используя эту формулу, можно записать вероятность спонтанного излучательного
Перехода атома, или вероятность спонтанного излучения для перехода, (в единицу времени) А = 1/тар в виде: '
167t3vgnH2 (2.3.19)
2 he0c3
Отметим также, что если обозначить через Nt полную плотность числа частиц в двух состояниях, или суммарную населенность этих состояний, то можно записать: N2(t) = Nta2(t)2 и iV2(0) = Nta2(0)|2. Умножая обе части (2.3.18) на Nt, получим: N2(t) = ЛГ2(0)ехр (~t/xsp) в соответствии с соотношением (1.1.2), которое было получено, исходя из общих соображений.