МОДЫ ПРЯМОУГОЛЬНОЙ ПОЛОСТИ
Рассмотрим полость прямоугольной формы, показанную на рис. 2.1. Для расчета функции ру определим вначале типы стоячих волн электромагнитного поля, которые могут существовать в данной полости. В соответствии с уравнениями Максвелла, напряженность электрического поля Е(х, у, г, £) должна удовлетворять волновому уравнению:
|
/ / |
7 7 |
С ~Та |
|
/-— |
||
|
Ь |
|
Рис. 2.1 Полость прямоугольной формы с идеально проводящими стенками, поддерживаемыми при постоянной температуре Т |
Где V2 — оператор Лапласа, а сп — скорость света в рассматриваемой среде. Помимо этого напряженность поля должна удовлетворять граничному условию на каждой из стенок полости:
Е х п = 0, (2.2.5)
Где п — нормаль к поверхности рассматриваемой стенки. Данное условие отражает тот факт, что для идеально проводящих стенок тангенциальная компонента электрического поля на стенках полости должна обращаться в нуль.
Нетрудно показать, что данная задача решается путем разделения переменных. А именно, если представить ее решение в виде:
Е = и(х, г/, z)E(t) (2.2.6)
И затем подставить выражение (2.2.6) в уравнение (2.2.4), то получим соотношение
У2ц = 1 d2E и с2 dt2 '
Поскольку левая часть данного равенства зависит только от пространственных координат х, у, г, тогда как правая часть зависит только от времени t, то для его выполнения при любых значениях пространственных и временных переменных необходимо и достаточно, чтобы обе его части были равны одной и той же константе, которую обозначим через - к2. Отсюда получаем два уравнения для функций и(х, у, г) и E(t):
V2 u = - fc2u, (2.2.7а)
D2E __ / l2 р
Df2 - Vn*) (2.2.76)
Уравнение (2.2.76) имеет общее решение вида:
Е = Е0cos (cot + ф), (2.2.8)
Где Е0 и ф — произвольные константы и
Со = спк. (2.2.9)
Поскольку функция E(t) описывается выражением (2.2.8), то решение (2.2.6) можно записать в виде:
Е(х, у, 2, О = Е0и(х, I/, г)ехру(со£ + ф). (2.2.9а)
Отсюда видно, что в произвольной точке пространства (х, у, г) напряженность электрического поля периодически изменяется во времени с постоянной амплитудой и(х, у, z), что соответствует стоячей волне электромагнитного поля внутри полости. Решение такого типа называется электромагнитной модой полости.
Приступим теперь к решению уравнения (2.2.7а), известного как уравнение Гельмгольца, учитывая при этом граничное условие, заданное соотношением (2.2.5). Нетрудно проверить, что выражения:
Их = excos kxx sin kyy sin kzz, (2.2.10a)
Uy = eysinkxx cos куу sin kzz, (2.2.106)
Uz = e^sin kxx sin kyy cos kzz (2.2. 10b)
Удовлетворяют уравнению (2.2.7a) при любых значениях ехУ еу, ег, если только выполняется равенство:
К2+к2+к2=к2. (2.2.11)
Для того чтобы получить окончательное решение, необходимо потребовать выполнения граничного условия (2.2.5). Отметим вначале, что выражения
(2.2.10) в том виде, как они записаны, уже удовлетворяют этому условию на трех плоскостях х = 0, у = 0, г = 0. Действительно, если взять, к примеру, плоскость г = 0, то условие (2.2.5) требует выполнения равенства их = иу = 0, и из (2.2.10а) и (2.2.106) видно, что оно справедливо, если положить 2 = 0. Если теперь потребовать выполнения условия (2.2.5) на трех других стенках полости, то получим:
|
|
Где I, тип — положительные целые числа. Действительно, если взять, например, плоскость г = Ь9 то условие (2.2.5) требует выполнения равенства их = иу = 0, и из (2.2.10а) и (2.2.106) видно, что оно справедливо, если положить г = Ь и принять во внимание (2.2.12в). Физический смысл чисел /, т и п заключается в том, что они представляют собой количество узлов, которые имеет мода стоячей волны вдоль направлений хууиг соответственно.
![]() Нетрудно заметить, что данные значения 1,тип однозначно определяют резонансную частоту моды. В самом деле, величины кх, ку и кг задаются соотношениями (2.2.12), и тогда, в соответствии с (2.2.9) и (2.2.11), угловая частота моды определяется соотношением:
Нетрудно заметить, что данные значения 1,тип однозначно определяют резонансную частоту моды. В самом деле, величины кх, ку и кг задаются соотношениями (2.2.12), и тогда, в соответствии с (2.2.9) и (2.2.11), угловая частота моды определяется соотношением:
(2.2.13)
В котором явно показано, что частота моды щтп зависит от индексов I, тип. Отметим, что мода при этом все еще не полностью определена, поскольку величины еХ9 еу и е2 пока еще остаются произвольными. Однако из уравнений Максвелла вытекает другое условие, которому должно удовлетворять электрическое поле, а именно V • и = 0, из которого, используя выражения (2.2.10), получаем равенство ехкх + еуку + е2к2 = 0. Это равенство можно кратко записать в виде:
Е • к = 0, (2.2.14)
Где введено два вектора е и к, компонентами которых вдоль осей х9 у и г являются величины ех, еуие2и кх9 ку и к2 соответственно. Используя равенство (2.2.14), можно показать, что из трех величин ех, еу и е2 только две являются независимыми. Действительно, если зафиксировать 19 тип (определив тем самым вектор к), то, согласно (2.2.14), векторе должен лежать в плоскости, перпендикулярной к. В этой плоскости для выбора вектора е остаются лишь две степени свободы. В самом деле, если обозначить через ^и|/ два произвольных ортогональных единичных вектора, лежащих в некоторой плоскости, то любой вектор е, лежащий в той же плоскости, можно представить в виде линейной комбинации этих двух векторов, т. е. е = е^ + е^у. Это рассуждение показывает, что заданным величинам 19 тип соответствуют две независимые моды, с одной и той же резонансной частотой и ортогональными поляризациями напряженности электрического поля.
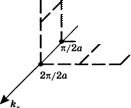
Определим теперь число резонансных мод АГ(у), частоты которых лежат в диапазоне от 0 до у. Это число будет равно количеству мод, волновой век-
|
2 п/Ь _____ |
|
/ /Г |
|
Рис. 2.2 Графическое изображение плотности числа мод в полости, изображенной на рис. 2.1. Каждая точка решетки соответствует двум независимым модам полости. |
|
2а |
|
Тельными, то необходимо учитывать только те точки, которые лежат в положительном октанте. Далее, как легко заметить, существует однозначное соответствие между этими точками и элементарными ячейками с размерами (я/2а, я/2а, п/Ь). Следовательно, число точек с величинами к, лежащими в диапазоне от 0 до (2п/сп)9 может быть определено как 1/8 отношения объема сферы с радиусом (2яу/с„), центр которой расположен в начале координат, к объему элементарной ячейки размерами (я/2а, я/2а, п/Ь). Поскольку, как уже говорилось выше, при каждом значении к существует две возможных моды, имеем: 14 Г 2яуЛ3 8 3 ^ сп ) _ 8яу3 |
|
Щу) = 2 |
|
-V, |
|
Я я я 2а 2а Ь |
|
JL. iL Зс„ |
|
Где V — объем всей полости. |
|
||
|
||
 |
||
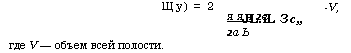 |
|
|
|
![]()
|
8яу2 |
![]()
|
Ру |
![]() (2.2.16)
(2.2.16)
Определив величину можно рассчитать ру как произведение числа мод в единице объема и в единичном частотном интервале на среднюю энергию (Е)9 заключенную в каждой моде, т. е.:
Р* = Р*(Е). (2.2.17)
Для вычисления (Е) предположим, что стенки полости поддерживаются при постоянной температуре Т. Согласно статистике Больцмана вероятность с1р
Того, что энергия данной моды полости лежит в интервале от Е до Е 4- dEy равна dp = C exp [-(.E/kT)]dE, где С — константа, удовлетворяющая условию
00
JCexp[-(E/kT)]dE = l.
О
Следовательно, средняя энергия (Е) моды равна:
$Eexp[-(E/kT)]dE
|
(2.2.18) |
![]() (.Е) = ^--------------------------- = *Г.
(.Е) = ^--------------------------- = *Г.
' 7 оо
Jexp[-(Ј//eT)]dЈ
О
Из соотношений (2.2.16) — (2.2.18) получаем:
( Snv2
|
3 |
![]() KT. (2.2.19)
KT. (2.2.19)
V С'
V
Полученное соотношение — это хорошо известный закон излучения Рэлея-Джинса. Однако эта формула полностью противоречит экспериментальным фактам. В самом деле, совершенно очевидно, что соотношение (2.2.19) ошибочно, поскольку оно приводит к бесконечно большой величине полной плотности энергии р (см. выражение (2.2.2)). Отметим вдобавок, что если бы оно было справедливо, то, в соответствии с (2.2.3), величина /у оказалась бы также пропорциональна V2, что означает неограниченное возрастание интенсивности излучения, испускаемого поверхностью черного тела при V —» оо (эту ситуацию иногда называют ультрафиолетовой катастрофой). Тем не менее, данное выражение является неизбежным следствием всех предыдущих рас- суждений в рамках классической теории.
Эти противоречия оставались неразрешенными до тех пор, пока Планк в начале XX века не высказал гипотезу о квантах света. Фундаментальная гипотеза Планка заключалась в том, что излучательный обмен энергией между стенками полости черного тела и ее внутренним пространством может происходить только дискретными порциями величиной Лу, где V — частота излучения, а Л — некоторая постоянная величина, впоследствии названная постоянной Планка. Минимальная порция энергии, которая может участвовать в процессе обмена, была позже названа квантом света, или фотоном.
Из гипотезы Планка однозначно следует, что энергия электромагнитной волны с частотой у может принимать не любые значения от 0 до оо, как это неявно предполагалось при выводе соотношения (2.2.18), а задается соотношением:
Е = пк у, (2.2.20)
Где п — положительное целое число. Следовательно, средняя энергия моды, как было показано Планком, равна
^ nhvexp[-(nhv/kT)]
<-E>='5_V = exp(ftv/AT)-l' (2.2.21)
2, exp[-(n&y /kT)]
71=0
Pv[10 16Джс/м3]
A
З -
2,5-

|
T=3000K |
![]()
|
J___ і__ т—■ і ____ і__ і ^ |
![]()
|
0 12345678 |
![]()
|
2 1.5 1 |
![]() Рис. 2.3
Рис. 2.3
|
0,5 |
![]() Зависимость функции ру (V, Т) от частоты V при двух значениях температуры Т
Зависимость функции ру (V, Т) от частоты V при двух значениях температуры Т
У[1014Гц]
Полученное выражение существенно отличается от классического представления (2.2.18). Очевидно, что при <С кТ (2.2.21) сводится к соотношению (2.2.18). Из соотношений (2.2.16), (2.2.17) и (2.2.21) можно вывести формулу Планка:
_ 8яу[4]______ hv_____
|
(2.2.22) |
![]() Pv с3 exp(/*v/&T)-l
Pv с3 exp(/*v/&T)-l
Которая полностью удовлетворяет экспериментальным результатам, при условии, что константа Л выбирается равной 6,62 • 10~34 Дж • с. В качестве примера на рис. 2.3 показано поведение функции ру в зависимости от частоты V при двух значениях температуры Т.
В заключение следует отметить, что отношение
|
|
(2.2.23)
Определяет среднее число фотонов (ф) в каждой моде в условиях теплового равновесия. Для частоты v = 4 х 1014 Гц, лежащей в оптическом диапазоне, hv * 1 эВ. При температуре Т » 300 К имеем кТ = (1/40) Эв, так что из (2.2.23) получаем, что (ф) = ехр (- 40). Таким образом, видно, что среднее число фотонов в каждой моде излучения черного тела при комнатной температуре оказывается намного меньше единицы. Это значение следовало бы сравнить с числом фотонов ф0, которое можно получить в одной моде резонатора лазера (ж Ю10, см. пример 7.1 в гл. 7).
На самом деле корректным. Однако прошло еще много лет, прежде чем гипотеза Планка была полностью подтверждена квантовой теорией поля Дирака (1927). И хотя подробное описание квантования поля выходит за рамки этой книги, уделим некоторое внимание тому, как оно проводится [2]. Это поможет лучше разобраться в некоторых вопросах, которые рассматриваются далее в этой книге.
Рассмотрим электромагнитную моду полости, то есть моду, описываемую заданной формой стоячей волны, и обозначим через V ее резонансную частоту. Если величины Ех{г, £) и Н^г, £) являются поперечными компонентами соответственно электрического и магнитного полей этой моды, то отвечающая им плотность энергии р определяется соотношением (2.2.1), а энергия в моде равна
|
|
(2.2.24)
Где V— объем полости. Прежде всего, для понимания основ квантовой теории поля необходимо осознать, что величины Ех(г, £) и Ну(г, £) не могут быть одновременно измерены с произвольной точностью [2]. Это означает, что существует соотношение неопределенности Гейзенберга для величин Ех(Г, £) И Ну(г, £), аналогичное тому, которое справедливо для положения рх и импульса дх частицы, движущейся, например, в направлении х.
Следует отметить, что соотношение неопределенности Гейзенберга для рх и qx является своего рода основой квантовой теории частиц. Действительно, оно показывает, что уравнения классической механики, которые основаны на канонических величинах рх и qx, неприемлемы в рамках квантовой теории. Аналогично соотношение неопределенности для Ех(г, £) и Ну(г, £) является основополагающим для квантовой теории излучения в том смысле, что оно показывает несостоятельность уравнений Максвелла, в частности уравнения (2.2.4).
|
(2.2.25) |
![]() Аналогия между квантовой теорией частиц и квантовой теорией излучения может быть продолжена, если рассмотреть частицу, связанную с заданной точкой пространства упругой силой. Это — случай квантового гармонического осциллятора, который представляет собой одну из важнейших моделей квантовой теории связанных частиц. Гармоническим осциллятором, колеблющимся, например, вдоль направления х, является механический осциллятор, полная энергия которого определяется выражением:
Аналогия между квантовой теорией частиц и квантовой теорией излучения может быть продолжена, если рассмотреть частицу, связанную с заданной точкой пространства упругой силой. Это — случай квантового гармонического осциллятора, который представляет собой одну из важнейших моделей квантовой теории связанных частиц. Гармоническим осциллятором, колеблющимся, например, вдоль направления х, является механический осциллятор, полная энергия которого определяется выражением:
Е = (крх /2) + (qx / 2т),
Где к — константа упругости, а т — масса частицы. Такой осциллятор имеет несколько общих черт с электромагнитной модой полости. И тот, и другая действительно являются осцилляторами в том смысле, что характеризуются резонансной частотой. В механическом осцилляторе колебания происходят из-за того, что потенциальная энергия, представленная слагаемым крх /2, периодически преобразуется в кинетическую энергию, описываемую слагаемым q2 /2т. В электромагнитном осцилляторе, которым является мода полости, электрическая энергия, представленная слагаемым J(e<^f)/2)dF, пе
риодически преобразуется в магнитную энергию, которая описывается как /2)(1У. Опираясь на эти аналогии, можно искать сходство и в правилах квантования. Корректно проведенная процедура квантования приводит к фундаментальному результату, который заключается в том, что энергия данной моды полости квантуется точно так же, как и энергия квантового гармонического осциллятора. А именно, собственные значения энергии моды записываются в виде:
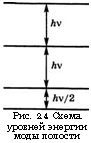
Е = (1/2)/гу + пк V, (2.2.26)
|
Рис. 2.4 Схема уровней энергии моды полости |
 Где п — целое число. Первый член — нулевая энергия в отсутствие колебательных квантов — имеет здесь то же происхождение, что и в случае гармонического осциллятора. Там этот член возникает, поскольку энергия осциллятора не может быть равна нулю, так как, согласно (2.2.25), это потребовало бы одновременного равенства нулю рх и дх, что, в свою очередь, противоречит принципу неопределенности Гейзенберга. Подобным же образом, в случае моды полости, энергия поля не может быть равна нулю, поскольку, согласно (2.2.1), это потребовало бы одновременного равенства нулю компонент Ех и Нх. Последнее невозможно также вследствие принципа неопределенности. Итак, квантование поля приводит к выводу, что значения энергии заданной моды полости (с частотой у) выражаются соотношением (2.2.26), что вполне соответствует гипотезе Планка (см. соотношение (2.2.20)), за исключением члена, отвечающего нулевой энергии. Таким образом, результаты квантования поля дают предположению Планка фундаментальное подтверждение. Излишне говорить о том, что уравнения Максвелла (см. раздел 2.2.1) не задают ни одного из условий, которым должна удовлетворять полная плотность энергии моды полости. В частности, согласно этим уравнениям энергия моды может непрерывно изменяться в интервале от 0 до оо, принимая любые значения.
Где п — целое число. Первый член — нулевая энергия в отсутствие колебательных квантов — имеет здесь то же происхождение, что и в случае гармонического осциллятора. Там этот член возникает, поскольку энергия осциллятора не может быть равна нулю, так как, согласно (2.2.25), это потребовало бы одновременного равенства нулю рх и дх, что, в свою очередь, противоречит принципу неопределенности Гейзенберга. Подобным же образом, в случае моды полости, энергия поля не может быть равна нулю, поскольку, согласно (2.2.1), это потребовало бы одновременного равенства нулю компонент Ех и Нх. Последнее невозможно также вследствие принципа неопределенности. Итак, квантование поля приводит к выводу, что значения энергии заданной моды полости (с частотой у) выражаются соотношением (2.2.26), что вполне соответствует гипотезе Планка (см. соотношение (2.2.20)), за исключением члена, отвечающего нулевой энергии. Таким образом, результаты квантования поля дают предположению Планка фундаментальное подтверждение. Излишне говорить о том, что уравнения Максвелла (см. раздел 2.2.1) не задают ни одного из условий, которым должна удовлетворять полная плотность энергии моды полости. В частности, согласно этим уравнениям энергия моды может непрерывно изменяться в интервале от 0 до оо, принимая любые значения.
В качестве заключения к данному разделу отметим, что согласно соотношению (2.2.26) уровни энергии моды полости, как и уровни гармонического осциллятора, можно изобразить, как показано на рис. 2.4. На самом нижнем, нулевом, уровне энергии как (Ех), так и (Нх) отличны от нуля. Эти величины называют нулевыми флуктуациями соответственно электрического и магнитного полей.
Отметим также, что сама по себе нулевая энергия (Лу/2) фактически не имеет физического смысла. Если вместо соотношения (2.2.24) определить энергию моды как
£ = (|р£ГГ)-(Лу/2), (2.2.27)
То самый нижний уровень будет иметь энергию, равную нулю. Однако можно показать, что соответствующему состоянию поля по-прежнему отвечают нулевые флуктуации (Ех)и(Нх) той же величины, что и прежде. Таким образом, именно эти флуктуации в действительности и являются характеристиками нулевого энергетического состояния.