ЯРКОСТЬ
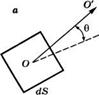
Определим яркость данного источника электромагнитных волн как мощность излучения, испускаемого с единицы поверхности источника в единичный телесный угол. Точнее, рассмотрим элемент dS площади поверхности источника в точке О (рис. 1.9а). Мощность dP, излучаемую элементом поверхности dS в телесный угол <2Q вблизи направления ОО', можно выразить в виде
DP = BcosddSdCl, (1.4.3)
 Где 0 — угол между направлением ОО' и нормалью к поверхности п. Отметим, что множитель cos 0 возникает из-за того, что физически важной величиной для мощности излучения в направлении ОО' является проекция элемента dS на плоскость, перепендикулярную направлению ОО', т. е. cos0dS. Величину Б, определенную с помощью соотношения (1.4.3), называют яркостью
Где 0 — угол между направлением ОО' и нормалью к поверхности п. Отметим, что множитель cos 0 возникает из-за того, что физически важной величиной для мощности излучения в направлении ОО' является проекция элемента dS на плоскость, перепендикулярную направлению ОО', т. е. cos0dS. Величину Б, определенную с помощью соотношения (1.4.3), называют яркостью
|
|
|
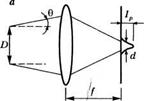
Рис. 1.9 (а) Поверхностная яркость в точке О произвольного источника электромагнитных волн, (б) Яркость лазерного пучка с диаметром И и углом расходимости 0 |
Источника в точке О в направлении ОО'. Эта величина зависит, вообще говоря, от полярных координат 0 и ф направления ОО' и от положения точки О. Если В является постоянной величиной, то источник называют изотропным (или источником Ламберта).
Рассмотрим теперь лазерный пучок мощностью Р с поперечным сечением в виде круга диаметром В, распространяющийся вдоль заданного направления (рис. 1.96). Вдоль этого направления яркость максимальна, а величина излучаемой при этом мощности определяется из соотношения (1.4.3), в котором сое 0 = 1. При конечных величинах площади 5 и телесного угла излучения О максимальную величину яркости можно выразить в виде В = Р/5П. Поскольку площадь поперечного сечения пучка равна кВ2/4, а телесный угол, в который происходит излучение, составляет я02, где 0 — угол расходимости пучка (предполагается, что расходимость мала), то в соответствии с (1.4.3) для максимальной яркости пучка получаем:
|
(1.4.4) |
![]() В = 4Р/(тс£>0)2.
В = 4Р/(тс£>0)2.
Отметим, что если пучок дифракционно-ограничен, то 0 = ва, и с помощью
(1.4.1) выражение (1.4.4) преобразуется к соотношению
|
|
(1.4.5)
Которое определяет наибольшую достижимую яркость пучка мощностью Р.
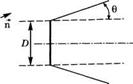
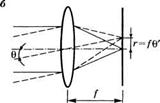
Яркость является наиболее важным параметром лазерного пучка и, вообще говоря, любого источника света. Для того чтобы проиллюстрировать это утверждение, напомним вначале, что если с помощью оптической системы формируется изображение какого-либо источника света, причем и объект, и изображение находятся в одной и той же среде (например, воздухе), то справедливо следующее: яркость изображения всегда меньше или равна яркости источника, при этом равенство сохраняется только в том случае, когда в оптической системе нет потерь света, испущенного источником. Далее, предположим, что пучок на рис. 1.96, с углом расходимости, равным 0, фокусируется линзой с фокусным расстоянием /. Рассчитаем интенсивность излучения в центре пятна в фокальной плоскости линзы (рис. 1.10а). Напомним, что для проведения расчета пучок можно представить в виде непрерывного набора плоских волн с распределением углов падения на линзу порядка 0 вокруг направления распространения. Две такие волны, пересекающиеся под углом 0', показаны непрерывной и пунктирной линиями на рис. 1.106. Каждая из волн фокусируется в пятно в определенном месте фокальной плоскости, и при малом угле 0' эти два пятна удалены на растояние г = /0'. Поскольку ширина распределения углов падения плоских волн, образующих пучок на рис. 1.10а, равна величине угла расходимости пучка 0, то можно положить диаметр фокального пятна на рис. 1.10а примерно равным <2 = 2/0. В случае идеальной непоглощающей линзы полная мощность излучения в фокальной плоскости равна мощности Р падающей волны. Таким образом, интенсивность излучения в центре пятна (пиковая интенсивность) достигает в фокальной плоскости величины 1р = 4Р/п<12 — Р/я(/0)2. Переходя к яркости
|
|
|
Рис. 1.10 (а) Распределение интенсивности В фокальной плоскости линзы для пучка с углом расходимости 0. (б) Разложение на плоские волны пучка, Изображенного в части (а) |
 Пучка с использованием соотношения (1.4.4), получаем 1р = (я/4)Б(£)//)2. Видно, что 1р возрастает с увеличением диаметра пучка В. Максимальная величина 1р достигается, когда В становится равен диаметру линзы Вь. При этом получаем:
Пучка с использованием соотношения (1.4.4), получаем 1р = (я/4)Б(£)//)2. Видно, что 1р возрастает с увеличением диаметра пучка В. Максимальная величина 1р достигается, когда В становится равен диаметру линзы Вь. При этом получаем:
1р = к{ЫА)2В, (1.4.6)
Где — числовая апертура линзы. Соотноше
Ние (1.4.6) показывает, что при заданной числовой апертуре пиковая интенсивность в фокальной плоскости линзы определяется только яркостью пучка.
Яркость лазера даже небольшой мощности (например, около нескольких мВт) на порядки превосходит яркость обычных источников света (см., в частности, задачу 1.7). Прежде всего этот факт является следствием высокой направленности лазерного пучка. В соответствии с соотношением (1.4.6) указанное различие означает, что пиковая интенсивность, получаемая в фокальной плоскости линзы, для лазерного пучка может быть на несколько порядков выше, чем для обычных источников света. Таким образом, интенсивность сфокусированного лазерного излучения может достигать огромных величин, что используется во многих областях применения лазеров.