Процессы и аппараты упаковочного производства
КОНВЕКЦИЯ И МАССООТДАЧА
Под конвективным массопереносом понимаю! процесс переноса вещества при движении жидкости или газа. Этот процесс происходит как бы механически - макрообъемными частицами жидкостного
Или газового потока.
Рассмотрим некоторые вопросы переноса массы внутри одной фазы, т. е. от ядра потока к границе раздела фаз или наоборот-от границы раздела фаз в ядро потока. Полагаем, что в нашем случае процесс массопереноса происходит между газом и жидкостью (процесс абсорбции, т. е. массоперенос идет из фазы Фу В фазу Ф^-), режим движения турбулентный.
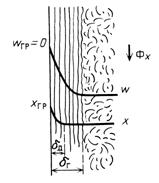
Гидродинамические особенности турбулентного потока в канале были рассмотрены в гл. 3. Здесь же следует отметить влияние гидродинамических условий на перенос вещества. В пограничном слое толщиной 8^ (рис. 15-2) происходит резкое, близкое к линейному изменение концентраций; поскольку в этой области потока скорость процесса определяется молекулярной диффузией, роль конвективной диффузии мала. Это объясняется тем, что на границе раздела фаз усиливается тормозящее действие сил трения между фазами и сил поверхностного натяжения на границе жидкой фазы. Образование гидродинамического пограничного слоя вблизи поверхности раздела фаз ведет к возникновению в нем диффузионного пограничного слоя толщиной 5д, обычно не совпадающей с 5^. В ядре потока массоперенос осуществляется в основном турбулентными пульсациями, поэтому концентрация распределяемого вещества в ядре потока практически постоянна. Как отмечалось выше, перенос вещества движущимися частицами, участвующими в турбулентных пульсациях, называют Турбулентной диффузией. Перенос вещества турбулентной диффузией описывается уравнением, аналогичным уравнению (15.14а):
![]()
Где U средняя пульсационная скорость движения частицы жидкости в поперечном направлении; /-расстояние, на которое перемещаются частицы в поперечном направлении; Бд = UI- коэффициент турбулентной диффузии.
Очевидно, что пограничный слой создает основное сопротивление процессу переноса.
Перенос по рассмотренной схеме называют Массоотдачей. По мере приближения к ламинарному режиму пограничный слой сильно разрастается, как бы заполняя все сечение потока. В этих
Рис. 15-2. Профили изменения скорости потока жидкой фазы (н7) и концентрации растворенного вещества (х) в турбулентном потоке
*с ювиях конвективный перенос идет в направлении, параллельном жнжению потока. При этом перенос массы к границе раздела определяется в основном молекулярной диффузией. Очевидно, что корость конвективного переноса существенно выше скорости мо-юкулярной диффузии. Поэтому развитие турбулентности способствует ускорению конвективного переноса массы.
Теоретическим путем толщину пограничного диффузионного юя можно определить для самых простых случаев массопереноса. Поэтому использование первого закона Фика
![]()
'(я описания процесса затруднительно, так как закон распределения концентраций в пограничном слое (дс/дп) неизвестен.
Массоотдачу, так же как и конвекцию, подразделяют на Естест-I Иную и Вынужденную, или Принудительную. При естественной массоотдаче движение жидкости происходит вследствие разности ц ютностей в разных точках жидкости, а при вынужденной - вслед -
Sane затраты энергии на движение потока извне-с помощью плсоса, мешалки и т. п. Очевидно, что естественная массоотдача-цюцесс медленный и в технике встречается редко, но часто является опутствующим процессом вынужденной массоотдачи.
По аналогии с эмпирическим законом охлаждения Ньютона ii 1И уравнением теплоотдачи) уравнение массоотдачи имеет еле-тощий вид:
![]()
К - (3^ коэффициент пропорциональности - коэффициент массоотдачи.
При установившемся процессе для всей поверхности F массо-ч дачи при т == 1 с уравнение (15.18) принимает вид
![]()
Для фазы Фу уравнение массоотдачи будет аналогично уравнению (15.18а), но с соответствующей заменой концентраций:
![]()
Из уравнений (15.18) и (15.19) найдем размерность коэффи-' центов массоотдачи:
![]()
Коэффициент массоотдачи показывает, какое количество вещества переходит от единицы поверхности раздела фаз в ядро отока (или наоборот) в единицу времени при движущей силе, равной динице.
Коэффициент массоотдачи, в отличие от коэффициента массо-!средачи, характеризует скорость переноса вещества внутри фазы конвекцией и молекулярной диффузией одновременно. Коэффициент массоотдачи зависит от многих факторов (физических
Свойств фазы, скорости потока, определяющих геометрических размеров и т. д.) и является аналогом коэффициента теплоотдачи. Ввиду сложной зависимости коэффициента массоотдачи от этих факторов получение обобщенной зависимости для определения величины ру или Р^ крайне затруднительно.
При разработке Моделей массопереноса обычно принимают допущение о том, что на поверхности раздела фазы находятся в состоянии равновесия, а общее сопротивление процессу переноса складывается из суммы сопротивлений двух фаз. Из этих допущений следует, что на границе раздела фаз отсутствует сопротивление процессу (т. е. равновесие на границе устанавливается очень быстро-во всяком случае, быстрее изменения средней концентрации в ядре фазы, что для ряда процессов массопереноса доказано экспериментально) и что процесс массопереноса подчиняется правилу аддитивности фазовых сопротивлений.
Вследствие взаимного влияния движения фаз, участвующих в процессе массопереноса, математическое описание скорости процесса чрезвычайно сложно. Поэтому решение дифференциальных уравнений переноса (см. гл. 3) оказывается возможным лишь в простейших случаях, когда точно известна поверхность контакта фаз и, как правило, при их ламинарном движении. В этом случае скорость процесса определяют совместным решением уравнений переноса в каждой из фаз.
Пленочная (двухпленочная) модель Льюиса и Уитмена основана на предпосылках, ранее рассмотренных Нернстом при изучении им растворения твердых тел в жидкостях. По этой модели с обеих сторон поверхности контакта фаз образуются неподвижные или ламинарно движущиеся пленки, в которых перенос вещества осуществляется только молекулярной диффузией. Эти пленки отделяют поверхность контакта фаз от ядра потока, в котором концентрация практически постоянна; все изменения концентрации вещества происходят в пленке.
В соответствии с пленочной моделью интегрирование уравнения (15.14а) приводит к выражению
![]()
Где §дд толщина пленки; Cq и ср-средняя концентрация в ядре фазы и концентрация на границе раздела фаз соответственно.
Сравнивая последнее уравнение с уравнениями (15.18) и (15.19), получим
![]()
Из уравнения (15.21) следует, что величина Р обратно пропорциональна толщине пленки, которая определяется гидродинамическими условиями: чем более турбулентны фазы, тем меньше бдд и, следовательно, тем выше р.
Уравнение (15.21) также показывает, что по пленочной модели коэффициент массоотдачи линейно зависит от коэффициента диф -
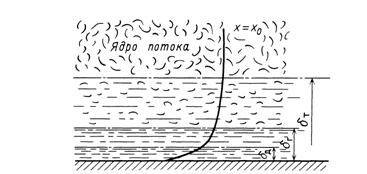
Рис. 15-3. К пояснению модели пограничного диффузионного слоя
J' ши, что часто не подтверждается экспериментально. Кроме того, ' < л теория не учитывает деформации поверхности контакта фаз переноса вещества турбулентными пульсациями.
В модели пограничного диффузионного слоя, которую 'ожно считать дальнейшим развитием пленочной модели, отра -
• 'чю влияние гидродинамических условий на процесс массопере-;^са. По этой модели (рис. 15-3) концентрация вещества, постоянен в ядре потока, в турбулентном подслое толщиной 8^ постепенно.(игжается при приближении к пограничному слою (т. е. в буферном ^дслое), в котором соизмеримы молекулярные и турбулентные и 1ы вязкости, т. е. v%v^. С уменьшением масштаба пульсаций
Вязком подслое толщиной 5^ концентрация снижается сущест -
- ино быстрее. В глубине вязкого подслоя, внутри тонкого Диффу-ушного подслоя толщиной 5д молекулярный перенос становится повным, при этом v » v^. Толщина пограничного диффузионного юя 8д меньше толщины вязкого пограничного слоя 5^, причем
![]()
С Т показатель степени, отражающий закон затухания турбулентного переноса |изи границы раздела фаз.
Для систем жидкость-твердое тело Т == 3, а для систем газ(пар)-идкость и жидкость-жидкость Т = 2. Поэтому [из уравнений (15.20) (15.22)] для систем твердое тело-жидкость М ^ D ' , а для систем н(пар)-жидкость и жидкость-жидкость М ~ D0'5.
Модель обновления поверхности фазового контакта ;scto называют моделью проницания, или пенетрационной. По гой модели предполагается, что турбулентные пульсации по-s оянно подводят к поверхности раздела фаз свежую жидкость смывают порции жидкости, уже прореагировавшей с газом чаром), т. е. каждый элемент поверхности жидкости взаимодействует газом (паром) в течение некоторого времени т (время контакта ' |и обновления), после чего данный элемент обновляется. На •гнове этой модели, принимая время т контакта постоянным для vcex элементов поверхности, Хигби получил уравнение для опре -
Деления коэффициента массоотдачи:
![]()
Как следует из уравнения (15.23), в отличие от пленочной модели скорость переноса по пенетрационной модели, как и по модели диффузионного пограничного слоя, М - D0'5, что подтверждается экспериментом.
Как и Хигби, Кишиневский принимает время контакта постоянным; за время контакта перенос вещества происходит посредством как молекулярной, так и турбулентной диффузии и описывается уравнением (15.23), причем коэффициент молекулярной диффузии D в уравнении (15.23) заменяется на сумму коэффициентов молекулярной и турбулентной диффузии, обозначаемую D^ .
Предложены и другие модели механизма массопереноса. Следует отметить, что их приведенные выше модели можно использовать для расчета процессов только в частных случаях, так как вследствие чрезвычайной сложности турбулентных двухфазных потоков практически невозможно определение в них поверхности контакта фаз, распределения концентраций в фазах и других параметров, необходимых для расчета.