Процессы и аппараты упаковочного производства
ТЕПЛООТДАЧА В ТУРБУЛЕНТНОМ ПОТОКЕ
Для анализа теплоотдачи в турбулентном потоке вводят понятие Турбулентной теплопроводности ![]() , которая является аналогом турбулентной вязкости
, которая является аналогом турбулентной вязкости ![]() в гидродинамике. Тогда удельный тепловой поток QT При турбулентном теплообмене в направлении оси Х (см. рис. 11-7) выразится так:
в гидродинамике. Тогда удельный тепловой поток QT При турбулентном теплообмене в направлении оси Х (см. рис. 11-7) выразится так:
![]()
Коэффициент турбулентной теплопроводности ![]() Т, Как и коэффициент турбулентной вязкости
Т, Как и коэффициент турбулентной вязкости ![]() T, не является физическим свойством среды, а определяется характером температурного поля, осредненными скоростями и другими внешними факторами.
T, не является физическим свойством среды, а определяется характером температурного поля, осредненными скоростями и другими внешними факторами.
В ядре потока ![]() , так как при этом количество теплоты, переносимое турбулентными пульсациями, значительно больше, чем молекулярной теплопроводностью. Очевидно, у стенки
, так как при этом количество теплоты, переносимое турбулентными пульсациями, значительно больше, чем молекулярной теплопроводностью. Очевидно, у стенки ![]() ,т = 0. Интенсивность переноса теплоты в ядре потока выражают с помощью коэффициента турбулентной температуропроводности Ат =
,т = 0. Интенсивность переноса теплоты в ядре потока выражают с помощью коэффициента турбулентной температуропроводности Ат = ![]() ,т/(рс), который уменьшается по мере приближения к стенке; в пограничном слое Ат < а, А у стенки Ат — 0. Принимают, что граница теплового пограничного слоя соответствует геометрическому месту точек, для которых Ат = А. Значения Ат И
,т/(рс), который уменьшается по мере приближения к стенке; в пограничном слое Ат < а, А у стенки Ат — 0. Принимают, что граница теплового пограничного слоя соответствует геометрическому месту точек, для которых Ат = А. Значения Ат И ![]() T, А И v обычно не совпадают, поэтому в общем случае не равны и толщины гидродинамического и теплового пограничных слоев, т. е.
T, А И v обычно не совпадают, поэтому в общем случае не равны и толщины гидродинамического и теплового пограничных слоев, т. е. ![]() . Эти слои совпадают лишь при
. Эти слои совпадают лишь при ![]() = А. Поскольку отношение V/A По существу представляет собой критерий Прандтля, так как Pr = V/A, То толщины гидродинамического и теплового слоев будут совпадать при Pr
= А. Поскольку отношение V/A По существу представляет собой критерий Прандтля, так как Pr = V/A, То толщины гидродинамического и теплового слоев будут совпадать при Pr ![]() 1, т. е. соблюдается подобие полей температур и скоростей и, таким образом, критерий Прандтля характеризует подобие этих полей.
1, т. е. соблюдается подобие полей температур и скоростей и, таким образом, критерий Прандтля характеризует подобие этих полей.
Одной из первых попыток увязать количество движения с конвективным переносом теплоты была сделана Рейнольдсом (1874 г.), который получил следующую зависимость:
St = ![]() /8, (11.39)
/8, (11.39)
Где ![]() - коэффициент гидравлического трения (здесь индекс «г» введен для того, чтобы отличить коэффициент трения от коэффициента теплопроводности
- коэффициент гидравлического трения (здесь индекс «г» введен для того, чтобы отличить коэффициент трения от коэффициента теплопроводности ![]() ).
).
Критерий Стэнтона характеризует отношение переноса теплоты теплоотдачей (т. е. конвекцией и теплопроводностью) к конвективному переносу.
St = Nu/(RePr) = Nu/Pe = A/(cpw) (11.40)
Зависимость (11.39) была получена при рассмотрении переноса теплоты и напряжения сил внутреннего трения в ламинарном пограничном слое и дает хорошее совпадение с экспериментом для случая Рг = 1. Позднее Прандтлем было получено уравнение для Рг ![]() 1:
1:
![]() (11.41)
(11.41)
Где W -скорость жидкости на границе пограничного слоя и турбулентного ядра потока. При Pr ![]() l уравнение (11.41) переходит в уравнение (11.39). Воспользовавшись выражением (6.31) для определения коэффициента трения
l уравнение (11.41) переходит в уравнение (11.39). Воспользовавшись выражением (6.31) для определения коэффициента трения
![]()
Получим
![]() (11.42)
(11.42)
Или
![]() (11.42а)
(11.42а)
Карман на основе гидродинамической теории теплообмена предложил уточненную формулу для определения коэффициента теплоотдачи, в которую не входит отношение скоростей W'/W:
![]() , (11.43)
, (11.43)
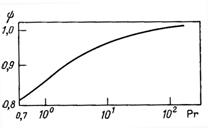
Коэффициент ![]() для потока в трубе зависит от критерия Рг (рис. 11-7). При Рг = 1 уравнение (11.43) переходит в уравнение (11.39). Теперь рассмотрим уравнение (6.28) гидравлического сопротивления при турбулентном движении потока в трубопроводе
для потока в трубе зависит от критерия Рг (рис. 11-7). При Рг = 1 уравнение (11.43) переходит в уравнение (11.39). Теперь рассмотрим уравнение (6.28) гидравлического сопротивления при турбулентном движении потока в трубопроводе
Eu=ARem(L/d)n
При П = 1. Так как сечение потока S = ![]() /4, а внутренняя поверхность F =
/4, а внутренняя поверхность F = ![]() DL, То L/D==F/4S. Перепишем выражение (6.28) следующим образом:
DL, То L/D==F/4S. Перепишем выражение (6.28) следующим образом:
Eu4S/F = ARem.
С учетом того, что ![]() Г = 2ARem, получим
Г = 2ARem, получим
EuS/F= ![]() /8. (11.44)
/8. (11.44)
С учетом (11.37) выражение критерия St примет вид
St = Nu/(RePr) = A1Rem-1Prn-1.
Обычно П = 1/3; тогда StPr2/3 = A'Rem-1.
Так как при Рг = 1 аналогия Рейнольдса дает St = ![]() г/8, примем, что A'Rem-1 =
г/8, примем, что A'Rem-1 = ![]() г/8. Тогда
г/8. Тогда
StPr2/3= ![]() (11.45)
(11.45)
Это выражение представляет собой аналогию Рейнольдса С Учетом поправки Рг2/3, учитывающей расхождение между подобием полей температур и полей скоростей. Выражение StPr2/3 КольборН обозначил буквой J И назвал Фактором теплопереноса, Который можно выразить так:
J= StPr2/3 = EuS/F = ![]() /8, (11-46)
/8, (11-46)
Или
![]() (11.46а)
(11.46а)
Количество теплоты, переносимое к стенке, Q = AF ![]() t; В то же время Q = Gc(TН - TK), Где TН И T К- начальная и конечная температуры теплоносителей. Следовательно,
t; В то же время Q = Gc(TН - TK), Где TН И T К- начальная и конечная температуры теплоносителей. Следовательно, ![]() . Тогда
. Тогда
![]()
Откуда
![]() (11.47)
(11.47)