Процессы и аппараты упаковочного производства
Уравнения фильтрования под действием перепада давления
Рассмотрим процесс фильтрования с образованием осадка. Скорость фильтрования W Определяют как производную объема фильтрата по времени τ, отнесенную к поверхности фильтрования S:
W = DV/(SDτ). (10.36)
При фильтровании суспензии вследствие небольшого размера пор осадка и фильтровальной перегородки и малой скорости движения жидкой фазы фильтрование протекает в ламинарной области. При этом в каждый момент времени скорость фильтрования прямо пропорциональна разности давлений ∆р И обратно пропорциональна вязкости жидкости и суммарному гидравлическому сопротивлению слоя осадка ROc И фильтровальной перегородки RФ. п:
W = ∆р/[μ(ROc + RФ. п)]. (10.37)
Приравнивая (10.36) к (10.37), получим основное дифференциальное уравнение фильтрования:
DV /(Sdτ) = ∆р/[μ(ROc + RФ. п)]. (10.38)
Для приведения уравнения (10.38) к виду, удобному для интегрирования, необходимо выразить величины ROc и RФ. п в виде функции объема фильтрата. В процессе фильтрования может происходить некоторое увеличение RФ. п Из-за проникновения в поры перегородки твердых частиц. Однако это увеличение незначительно, так что для практических целей можно считать = Const. Величина с возрастанием толщины слоя осадка изменяется от нуля в начале фильтрования до максимального значения в конце его. Пренебрегая влиянием гравитационного осаждения (под действием сил тяжести) на образование осадка, можно считать, что объем осадка, VOc Прямо пропорционален объему фильтрата V:
VOc = Хо V , (10.39)
Где Хо - коэффициент пропорциональности, зависящий от концентрации твердой фазы и структуры осадка (его определяют экспериментально как объем осадка, образующегося при прохождении 1 м3 фильтрата).
Представим объем осадка как произведение HOcS (где HOc - Высота слоя осадка). Тогда
HOcS = хо V, (10.40)
Откуда
HOc = хо V /S. (10.41)
Представим теперь сопротивление слоя осадка как произведение
ROc = RОHOc, (10.42)
Где RО - удельное объемное сопротивление слоя осадка (м-2), т. е. сопротивление, оказываемое потоку жидкой фазы слоем осадка толщиной 1 м.
Подставляя в соотношение (10.42) высоту осадка, определяемую по (10.41), получим выражение, связывающее сопротивление осадка с объемом фильтрата:
ROc = RО хо V /S (10.43)
Перепишем выражение (10.38) с учетом (10.43):
![]() =
= 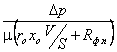 (10.44)
(10.44)
Решая это дифференциальное уравнение, можно получить уравнения фильтрования для различных частных случаев. Поскольку большинство фильтров работает при постоянной разности давлений, а процесс промывки можно рассматривать как фильтрование при постоянных разности давлений и скорости, ограничим рассмотрение этими двумя вариантами.
Уравнение фильтрования при постоянной разности давлений. Перепишем выражение (10.44) в следующем виде:
Хо V /S + RФ. п)dV = ∆РSdτ
Проинтегрируем левую часть от 0 до V, А правую - от 0 до τ, вынеся постоянные величины за знак интеграла:
![]()
![]() + μRФ. п
+ μRФ. п ![]() = ∆PS
= ∆PS ![]() ;
;
(μRО хо/S)( V2/2) + μRФ. пV = ∆рSτ
Разделив последнее выражение на μRО хо/(2S), Получим:
V2 + 2RФ. пSV/(RО хо) = 2∆рS2τ/(μRО хо) (10.45)
Это уравнение называют уравнением фильтрования при постоянной разности давлений.
На практике часто можно считать сопротивление фильтровальной перегородки пренебрежимо малым по сравнению с сопротивлением осадка. Тогда уравнение (10.45) принимает вид:
V2 = 2∆рS2τ/(μRО хо). (10.46)
Уравнения (10.45) и (10.46) применимы как к несжимаемым осадкам, так и к сжимаемым, поскольку при ∆Р = const значения RО И хо в процессе фильтрования остаются постоянными. Из уравнения (10.46) видно, что объем фильтрата возрастает пропорционально квадратному корню из времени.
Уравнение фильтрования при постоянных разности давлений И скорости. При постоянной скорости отношение dV/dτ можно заменить отношением V/τ. Кроме того, поскольку рассматриваемый процесс осуществим только при постоянной толщине слоя осадка, заменим XoV/S На высоту слоя осадка HОс. С учетом сказанного уравнение (10.44) примет вид:
V/(Sτ) = ∆р/[μ(RО HОс + RФ. п)],
Откуда
V = ∆рSτ/[ μ(RО HОс + RФ. п)]. (10.47)
Уравнение (10.47) представляет собой уравнение фильтрования при постоянных разности давлений и скорости. Оно применимо для несжимаемых и сжимаемых осадков.
Для выполнения расчетов по уравнениям (10.45)-(10.47) необходимо экспериментально определить величины RО и RФ. п и затем ХО, носящие название Констант фильтрования.
Рассмотрим один из способов определения этих величин. Разделим все члены уравнения (10.45) на 2∆PS2 V /(μ ROXO) и поменяем местами левую и правую части уравнения:
τ/V = μRО XOV /(2∆PS2) + μ RФ. п /(∆PS) ( 10.48)
Введем обозначения:
μRО XO /(2∆PS2) = M; (10.49)
μRФ. п /(∆PS) = N. (10.50)
При постоянных разности давлений и температуре все величины, входящие в правые части равенств (10.49) и (10.50), являются постоянными. Таким образом, М = const и N = Const. Теперь перепишем выражение (10.48):
τ /V = MV+ N. (10.51)
Это уравнение показывает прямолинейную зависимость функции τ /V От аргумента V. Тангенс угла наклона прямой равен М, А отрезок, отсекаемый на оси ординат, - N.
Для определения этих величин проводят эксперимент на модельном фильтре, в процессе которого замеряют во времени объем полученного фильтрата. Обработкой данных по методу наименьших квадратов рассчитывают М И N, А затем с помощью выражений (10.49) и (10.50) находят RО и RФ. п. Кроме того, в эксперименте замеряют объем осадка на фильтре и рассчитывают ХО по соотношению Хо = VOc/ V.
При фильтровании суспензий, содержащих монодисперсные частицы большого размера (порядка нескольких миллиметров), значение RО можно вычислить по уравнению (6.72). Для этого, исключив, из уравнения (10.37) сопротивление фильтровальной перегородки, представим его в следующем виде:
W = ∆р/(μRО HОс), (10.52)
Откуда
RО = ∆р/(μ HОсW). (10.53)
Подставляя сюда ∆Р, Определяемое по (6.72) с учетом того, что Н = HOc И Wo = W, Получим:
RО = 150(1 - ε)2/(Φ2ε3D2). (10.54)