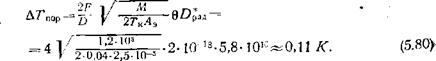Фотоприемные устройства и ПЗС. Обнаружение слабых оптических сигналов
ТЕПЛОВИЗОР
Тепловизор предназначен для преобразования теплового изображения и различения разности температур АТ нагретых тел. Для темы нашей книги важна температурная чувствительность — минимальная разность температур, которую способен зарегистрировать тепловизор. В соответствии с принятой нами терминологией назовем ее пороговой разностью температур
ДТ'пор она вызывает сигнал, равный шуму, В литературе при- нят термин «эквивалентная шуму разность температур» и соответственно ее обозначения NEAT, NEDT (Noise Equivalent Diffйrence Tempйrature) [9,114].
В предыдущих параграфах оптический сигнал ФП всегда был задан. Теперь задается разность температур объектов, наблюдаемых тепловизором. Поэтому наш анализ надо начи - нать с расчета оптического сигнала — потока теплового излучения, принимаемого ФП.
Излучение тела, слабо нагретого относительно фона. Рассмотрим идеализированную модель: фон однороден и излучает как абсолютно черное тело с температурой Т. Спектральная плотность излучения такого фона п(к) определяется законом Планка (1.30). Эта модель фона уже использовалась в § 1.2, 3.4 при расчете фоновых токов и радиационной обнаружитель - ной способности. Теперь дополнительно введем объект — тело, слабо перегретое относительно фона на температуру АТ— ~Т0б—Т. Поэтому спектральная плотность излучения объекта выше, чем фона, на величину
Е &Ti (А) ^ ^ д
Оп= dT а/ г [ехр (а«/*гл,>— Г] "
2лс hc ехр (hcjkT'k) ^
Я.4 [ехр (Ас/ftГЯ) —11 ехр (hcjkTX)—1
J^nlQbT. (5.37)
КТ2 А
Здесь при расчете производной dnfdT пренебрегли единицей по сравнению с большим экспоненциальным членом (ехр (hc/kT’k)~^3,b при 5^14 мкм, 7=293 К (1-34).
Если ФП селективный (регистрирует фотоны в узком спектральном диапазоне к'.. . к'--dk), то значений гс(Х), бп(к) вполне достаточно для расчета сигнального и фонового токов. В общем случае, когда ФП регистрирует фотоны в широком спектральном диапазоне к'...к", надо проинтегрировать п(к) и 6п{Х) в этом диапазоне. В § 1.2 для числа фотонов #эф> испускаемых АЧТ в интервале длин волн к' . .. к", были получены аналитические выражения (1.34) — (1.38). Для дополнительного излучения объекта, перегретого относительно фона на Д7 используя (5.37), можно получить
«ЛГэф = $ &ге(Х.)<Л = ^Ц^Л. ■ (5.38)
Функция п (к) в числителе подынтегрального выражения при А<9 мкм (7 = 293 К) очень резко растет с длиной волны по сравнению со слабо меняющимся знаменателем Я. Поэтому основной вклад в интеграл дает площадь под кривой п{к) в
379
Окрестности %=%". Знаменатель здесь можно полагать постоянным, равным л" и вынести его из-под знака интеграла. В диапазоне Я" = 9... 14 мкм скорости изменения функций п(>.), л сопоставимы и для оценки предельных значений интеграла следует выбирать минимальное (Ятш = 9 мкм) и максимальное Х'г значения числителя. Так что получаем следующую оценку:
ЬМ
Впрочем, значение бЛ^ф можно не только оценить, но и достаточно точно рассчитать, так как зависимость Л^ф (Т) была рассчитана в § 1.2. Пользуясь для NЬф{T) аппроксимацией
(1.50) , получаем
Я* %'
ЙЛГэф= ? ЛДТ=-^т пйХТ = ^-ДТ, (5.40)
А/ V
|
Формулу для Е, (1.51) здесь удобно преобразовать следующим образом: |
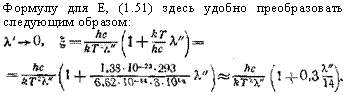 ^=^Л^5ф(7')ехр(|Д7’)|д7-.о = Дг8ф1. (5.41)
^=^Л^5ф(7')ехр(|Д7’)|д7-.о = Дг8ф1. (5.41)
Значение Я" в круглых скобках нужно выражать в микрометрах. С учетом такого представления £ (5.40) принимает вид
Сопоставляя все три полученных выражения (5.37), (5.39) ^ (5.43), можно сформулировать общую закономерность: приращение излучения слабо перегретого объекта (относительного фона) пропорционально излучению фона и обратно пропорционально длине волны Xй. Это относится к излучению объекта и в узком спектральном диапазоне и в широком. 'к" (правда, в последнем случае зависимость бА^оо 1Д" выполняется с точностью до 30%). В дальнейшем воспользуемся указанной^ закономерностью, она существенно упростит расчет пороговой разности температуры.
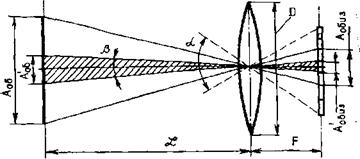
Отношение сигнал-шум. Объектив тепловизора формирует изображение в фокальной плоскости (на ФП) с уменьшением где 2? — расстояние между объектом и объективом; Р —
|
|
|
А) |
|
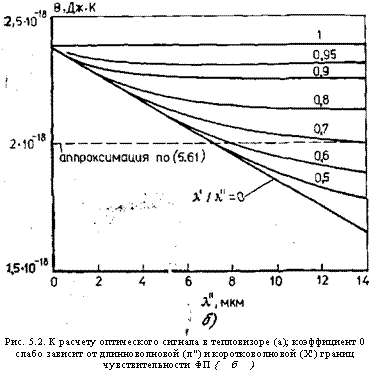
Рис. 5.2. К расчету оптического сигнала в тепловизоре (а); коэффициент 0 слабо зависит от длинноволновой (л") и коротковолновой (X') границ чувствительности ФП {б) |
 |
фокусное расстояние (рис. 5.2, а). При размерах и площади объекта £,обХ^об = ^об получим соответственно для размеров и площади его изображения
1о6и,= (/:'/2’)^ов; Лобиз=£об»3Х£о«„з=(Я2>)2Ло6. (5.44)
381
Пусть избражение объекта перекрывает несколько элементов ФП. На один элемент с площадкой Лэ приходит излучение только с части поверхности объекта А0б':
Аэ=(Гт2Аоб'. (5.45)
С помощью законов энергетической фотометрии нетрудно подсчитать число фотонов, приходящих на один элемент с этой поверхности Лоб'. Поверхность является источником излучения с силой света в нормальном направлении (выражаемой в числе квантов), равной
Облученность на объективе согласно закону квадрата расстояний (закону Бугера) равна
А0б (ЛЛ, ф + 6/Уэф)/я^2. (5.47)
Тогда число фотонов, собираемое на элемент объективом диаметром О (диаметром входного зрачка), составляет
|
= Т-5г(^Ф + ^У9ф) = |
![]() Ло2 Аоб (А^ф + бЛ^эф) £>*Аоб
Ло2 Аоб (А^ф + бЛ^эф) £>*Аоб
4 4 &
= 4ТГ лэ (Агэф + 6/Уэф). (5.48)
Формула (5.45) помогла нам избавиться от неудобных, произвольно меняющихся параметров объекта Л0б', 3? — их заменили на известные параметры тепловизора Ай, Качественно последнее выражение можно получить из законов сохранения: если бы испускаемые объектом фотоны равномерно распределялись по площади полусферы 2лЗ?2> то на объектив площадью л0214 приходилась бы следующая часть от общего числа этих фотонов:
Однако в нормальном направлении испускание оказалось вдвое сильнее этого усредненного значения.
^Составляющая потока создает фоновый ток /Тф, та
Кой же, как при облучении от однородного фона, Дополнительный поток ои 6Л^Эф за счет перегрева объекта создает фототок сигнала /с:
/, = *3£«ли=^(*^*ДГ), Ч, (5.50)
Эти выражения записаны для принятой идеализированной модели: ФП является идеальным счетчиком фотонов в заданном спектральном интервале от V до (кривая 2 на
Рис. 1.7).
Последующая обработка сигнала происходит так, как было описано в § 4.5, 4.6. В тепловизоре имеем дело с классическим случаем обнаружения прямоугольного сигнала (на фоне белых шумов). Понятно, почему форму сигнала можно считать прямоугольной: при использовании матрицы в отсутствие сканирования облученность каждого элемента остается постоянной в течение заданного времени. кадра Тк. Но и при сканировании (линейкой или одноэлементным ФП) сигнал остается постоянным между двумя опросами, поскольку элемент перемещается на шаг I, меньший изображения объекта. Интервал между опросами будет равен ТКМЭ/М, гдеЛ! — число элементов разложения изображения; Мэ — число фоточувствительных элементов ФП (4.287). Этот интервал можно принять за длительность импульса Гс. Для такой задачи идеальным фильтром является накопитель с временем накопления Тк = Тс = ТкМэ/М (§ 4,6). За время Тн накапливаются заряды сигнала С^ = 1сТк и фона С2о = 1(}Тн — последний ответствен за шум, так что искомое отношение сигнал-шум будет с учетом (4.237), (5.50),,
|
Q-^r-ЫТ |
|
1СТН 4 F* * ат |
![]()
|
~[ о^н '^/rO/A37'i] |
![]() <Nzfui'
<Nzfui'
4/7Ь <7'^эф
D VА32Т~Н дN^/dT
- ------ ™, А т ' (5.52>
2F y2NЗф
Пороговая разность температур идеального тепловизора. Из
Последней формулы для отношения iVc/Ui согласно определению получим следующее выражение для пороговой разности температур идеального тепловизора [115]:
АТ 2F 1 Vл - «у.
Ы раД_^с/ш “ D УТэ(2Та) дN^/dr У ' }
Индекс «рад» означает, что формула записана для радиационного предела — режима ограничения флуктуациями фона, когда А7ПОр—АТрад.
Наша предварительная алгебраическая работа завершена. Теперь можно провести презентацию полученного выражения— представить по очереди каждый из трех его сомножителей.
Первый сомножитель 2F/D. Так как в тепловизоре исходный оптический сигнал задается не на поверхности ФП, а на объекте, то к цепочке преобразований оптического сигнала в электрический подключился объектив. Поэтому в формулу
(5.53) вошло относительное отверстие D/F. Чем она выше, тем, естественно, лучше температурная чувствительность тепловизора.
Второй сомножитель 1/~|/Л9(2Тн). Характеризует тепловизор как трехмерный фильтр-накопитель — в пространстве (по осям х я у) и вэ времени (по оси *)• Соответственно в формулу для 47рад вошли интервалы накопления в пространстве Лэ и во времени Тп (точнее, вошла эффективная полоса частот фильтра-накопителя 1/(2 Гн) (табл. 4.1). Рассматриваемый множитель можно модифицировать на любой вкус, если выразить время накопления через время кадра ГН~7КМЭ/М (4.287), площадь элемента согласно (4.283) заменить площадью кадра АЭ=А/М (когда матричный ФП занимает всю площадь кадра, то А одновременно является и площадью ФП) и, наконец, ввести частоту кадров /к=1/7'к:
SHAPE \* MERGEFORMAT ![]()
![]()
|
М |
![]()
|
‘2ТКМЭА3 у 2ТкМэА |
Набор этих выражений показывает, что пороговая разность температур ухудшается с ростом разрешения, частоты кадров и с уменьшением площадки элемента, а улучшается с ростом числа элементов (при Мв->-М). Все эти зависимости элементарным образом объясняются изменением накопления теплового излучения во времени и пространстве при вариации указанных параметров.
На пределе разрешения, когда перегретый объект проецируется на один элемент, возникают неприятности из-за распределения энергии между соседними элементами и кадрами (§ 4.5, 4.6), так что ДТпор может стать хуже (вплоть до 4 раз) но сравнению со значением, рассчитанным по формулам
(5.53) , (5.54). В режиме пирометра, когда надо определить только температуру объекта с точностью около ДТпор> а конфигурация и площадь объекта Л0б заранее известны, можно накапливать сигнал по всем облученным элементам, так что в формулу (5.53) вместо площади элемента Лэ войдет площадь изображения объекта Л0виз.
Отметим, что формулу (5.53) можно использовать также для расчета погрешности измерения температуры с помощью радиационного пирометра на основе одноэлементного ФП. В этом случае Лэ является площадью ФЧЭ.
Для проектировщика тепловизора может быть полезной связь ДТ'цор с угловым разрешением (углом поля зрения одного элемента) у Аэ/Г и всем полем зрения тепловизо
|
<5.55) |
![]() Ра а =*УА/Р (рис. 5.2, а). Эту связь можно найти преобразованием двух первых сомножителей:
Ра а =*УА/Р (рис. 5.2, а). Эту связь можно найти преобразованием двух первых сомножителей:
|
|
° Уа9&т$ .
|
|
Все эти и подобные им преобразования позволяют провести анализ ДТпор в зависимости от группы параметров, которые можно назвать параметрами тепловизора как ячеистой антенны для электромагнитного излучения оптического (теплового) диапазона — от площади, угла зрения, числа ячеек и т. д.
Третий сомножитель в (5,53). Он представляет собой пороговую разность температур гипотетического тепловизора с единичным значением 2Р/0= (при котором ФП принимает тепловой поток из полусферы 2 л стерадиан), единичной полосой частот накопителя 1/2 7^=1 с~ единичкой площадкой фотоэлемента ;4Э=1 см2. Или, иначе, это удельное приведенное значение пороговой разности температур:
* ЛТ’рад У2Л^зф
Рал 1 — !йТ *
° I ЛЭ(2Г1;)
Для нас рассматриваемый множитель является основным, так как показывает связь температурной чувствительности тепловизора ЛТрЯЛ с пороговыми свойствами ФПУ.
Как уже отмечалось, ФПУ, которое вошло в состав идеального тепловизора,—это оптимальный обнаружитель прямоугольного сигнала. Числитель (5.57) У 2Мэф представляет собой спектральную плотность шума такого ФПУ, а знаменатель йМ^ф/йТ — амплитуду сигнала'. Шум и сигнал выра&ены здесь в числе эффективных квантов. Пороговые свойства такого ФПУ характеризуются удельной радиационной обнаружительной способностью Орал (§ 3.4). Попытаемся найти связь между параметрами ДТрах И Оряд.
Основное тепловизионное соотношение. Прежде всего
Выразим величину Ор31 (3.112) через число эффективных квантов М, ф:
Рад1 ; V 2д/тф яс У2д-д^Эф ьсУ'Жэф
Здесь воспользовались формулой 3 = цУ*1кс (1.3). Из сравне - ния (5.57) и (5.58) становится очевидным, какую манипуляцию надо проделать с выражением для АТрЗД (5.57), чтобы в нем появилась обнаружительная способность:
УшГф _ Кс-2АГэф__________
Л раД^йЛГэф/йГ^ ЬЛ<<Шаф 1йТ) ь. сУ
25—4946
Второй множитель в правой части как раз и является величиной Орад. Остается проанализировать первый множите^* — коэффициент 9:
/гс-гл'эф 1 Не-2ДГЭф кТ2к" ^
9= >7 5аЦ75г= кг лс (1+(а г/лс) ?."] ^эф
Да 2^ [ 1 - (* 77йе) V'] = 24 Г* Г1 - 0,3 . (5-60)
В преобразовании (5.60) воспользовались зависимостью с1АгЭф/ЗТ со Л^эф/Л" (5.43), которая была заранее подготовлена в начале параграфа. Благодаря такой зависимости параметры Л/эф и сокращаются и в результате оказывается, что 0 очень слабо зависит от длины волны Я". Согласно (5.60) в рассматриваемом весьма широком диапазоне Я" = 3... 14 мкм коэффициент 0 изменяется (уменьшается) всего на 30%. С достаточной для многих практических расчетов точностью этот коэффициент вообще можно считать постоянным и равным его среднему значению в диапазоне 3 ... 14 мкм;
0 да 0- 2к Тг [Т=0Ж77Щ:= 2£ Р0,85=
= 2- 1,38-10-23(293)20,85-2-10'18(ТУ293)2Дж-К. (5.61)
Напомним, что при расчете 6(?ь") использовалась зависимость Мэф(Х") для идеального ФП с широким спектральным диапазоном О...?/' (1.35), (1.36). Если чувствительность ФП ограничена не только со стороны длинных волн (}/'), но и со стороны коротких (?/), то надо использовать для Л^ф^/Д") формулы (1.35) — (1.38). Получаемые при этом аналитические выражения для 6(Х',?/') достаточно громоздки, так что удобнее: пользоваться рис. 5.2, б. где представлены результаты численного расчета этой зависимости. Как видим, в пределе при коэффициент 0 вообще перестает зависеть от >/, X" и стремится к своему максимальному значению 2 кТ2, так что для селективного ФП 0 является константой. Этот интересный результат следует непосредственно из выражений (5.37), (5.60). При этом #эф(л"—Я") = п(Х'')с1Х, поэтому
А_.Лс2ЛЧ _____ 1 У'кТ* __9,
' I" Нсп{У') ' ’ )
Таким образом, приближенное выражение (5.61) оказалось справедливым для ФП с любыми значениями Я', X" (не превышающими 14... 15 мкм при температуре фона 293 К).
Теперь перепишем выражение для Л7*ад (5.59) в окончатель - ном виде, к которому мы стремились:
Теория обнаружения представляет еще одно правило — тепловизионное соотношение (5.60) — (5.63) [115]:
Удельная пороговая разность температур идеального тепловнэсра ДГр*ад равна удельной радиационной обнаружительной способности Ф П У Х>радг множенной на коэффициент 9 Коэ(Ь* фицнент 0 йочти не зависит от спектрального диапазона: для селективного ФП он постоянен и равен 2кТг, а для ФП с широким спектральным диапазоном меняется в достаточно малых пределах ±15% (вблизи этого же значения 2&Г2).
Ограничения на значения ДТрад, £>£ад накладывает не тепловизор и не ФПУ, а сам объект наблюдения — флуктуации теплового излучения объекта. Предельная температурная чувствительность тепловизора ДГрад является фундаментальной величиной. Попытки достичь чувствительности лучше предельной величины АТрад — это попытка построить вечный двигатель (что уже отмечалось в § 3.4 относительно /)£ад для ФПУ). Согласно тепловизионному соотношению предельная температурная чувствительность ДТ^рад зависит только от двух параметров выбранного спектрального диапазона и температуры
Фона Т. Рассмотрим последовательно эти зависимости.
Температурная чувствительность и спектральный диапазон. Во избежание тавталогии не будем приводить зависимость ДТ'рад так как согласно тепловизионному соотношению она С точностью ±15% воспроизводит зависимость /}рад М - С расширением спектрального диапазона (до 9... 10 мкм) температурная чувствительность тепловизора резко улучшается (значение АГрах уменьшается), что объясняется резким возрастанием числа эффективных ФоТонов А^эф. При возрастании Агэф шум увеличивается ^УА^ф, однако сигнал РасТет сильнее.
Так что их отношение соуд^эф. В области
10.. . 14 мкм зависимости Агэф(Х/г) и соответственно ДГрад(Я" становятся более плавными. Теоретически наилучшая чувствительность достигается, когда ФП регистрирует все фотоны фона, т. е. при Согласно закону Стефана—Больцмана пол
Ное число фотонов АЧТ (излучаемое с единицы поверхности во всем диапазоне спектра) равно а'Т3 (1.41), поэтому для температурной чувствительности (5.59)
TOC o "1-5" h z АГ. У^~Ф Уыт* I 1/~Г - #•
А1 рад — за'7-2 з У о'Т ■ ;
__ ----- = 7, Ы О'8 VК • см • с112. ,(5.64)
3 У 1,59-Ю11 -293 1 У Т ' )
Физика «обвиняет» нас в пренебрежении ее законами при выводе последнего уравнения: дисперсия числа фотонов в этом уравнении рассчитывалась для пуассоновского распределения.
Но такое распределение справедливо до длин волн 14 ... ...15 мкм, т. е. до тех-пор, пока ехр [hcfkTX) > 1. На более длинных волнах сказывается группировка фотонов, что приводит к увеличению дисперсии в exp (hcfkTX)[exр (hcfkTX)—1] раз по сравнению с принятым нами значением 2n(X)dX [33].
|
/ „ С яд)ехр(Д/*7Ч) / ехр(/мг/А7Ж)~1 / --------------------- i ^“ Со, , i 2f п(ЩХ Ц Г - р — |

![]() Первый довод эдикты,-'Действительно, с учетом сверхпуас - соновского шума величина А7*рад должна увеличиваться в F раз:
Первый довод эдикты,-'Действительно, с учетом сверхпуас - соновского шума величина А7*рад должна увеличиваться в F раз:
/ f exp (Ас/А ГЯ) /С ^ ехР
TOC o "1-5" h z ![]() / J л4 [ехр (Ас/£7Ч) — 1]ь d ' "I/ 3 (ехР*/— О"
/ J л4 [ехр (Ас/£7Ч) — 1]ь d ' "I/ 3 (ехР*/— О"
/ -------- !----- =, I/ - J-------------------------- -
ОО •■••• Г у
F dXj№ [ехр (kc/kTX)%^] f у2 d у/(ехр fir—1)
О ь 5
![]() - *.•----------------- =—
- *.•----------------- =—
212 Л'2/2! 2 те"3 = 7^1.65/1,20 = 1,17. (5.65)
/гг=1 ' I t
Как видим, сверхпуассон^бсрдае шумы хотя и приводят к увеличению ДГрад при Л"^-Ьь/нО всего на 17%.
Второй довод защиты. ” Численный расчет зависимости Д7^ад(л") с учетом сверхпуассоновского шума показывает наличие в ней слабо выраженного минимума на длине волны 28 мкм. Этот минимум всего на 3% превышает значение (5.64). Так что уточненное значение Д7рад почти не отличается от прежнего, полученного в приближении пуассоновского распределения:
X"=2s(~J мкм, min Д7^;1Л"7,3- 1СИ ]/^ К-см-с1'2. (5.66)
Это последнее в нашей книг£ соотношение теории обнаружения, определяющее абсолютный предел температурной чувствительности тепловизора. А б g;b л ютный предел не зависит от спектрально го диапазона и является функцией только одной физической величины — те мпер ату р ы ф о на [115].
Соотношение (5.66) не ставит перед разработчиком тепловизора сверхсложной задачи —обязательно покорить дальний ИК-диапазон 28 мкм. Как уже отмечалось, при //'> 10 мкм зависимость Д7'^ад(А,-й) становится слабой, значения ДГрад близки к min ДГрад. Достаточно использовать ФП V спектрального диапазона с длинноволновой границей 10, 12 либо
14 мкм. Численный расчет показывает, что тепловизоры с такими ФП «недотягивают» до абсолютного предела’всего 35, 20 и 12% соответственно. ,
Основные теоловизионные соотношения (5.63), (5.66) описывают теоретическую зависимость Д7‘рад(Я//) во всем диапазоне изменения Я//[0, оЦ. Соотношение (5.63) справедливо в диапазоне значений Я"=Ц)...Яь а (5.66) можно считать апроксима - цией при Яу/>Яь причем
* ПлЛс п ч 6,62-Ю1» ^е/293.
Я1~0,3АГ-0,3 ” ]>38.ю-23.293 ( Т )’ ^ ,67)
Здесь Я] выражено в мкм; Г — в К-
Так как температурная чувствительность повышается с расширением спектрального диапазона (особенно резко при переходе от 2 ... 5 до 8 ... 14 мкм), то разработчики тепловизоров стремятся к повышению длинноволновой границы Я", освоению области 8... 14 мкм, тем более что в этой области меньше поглощение в атмосфере. Однако на практике повышение Я" связано с рядом трудностей: необходимо применять более глубокое охлаждение, усложняется технология ФП. Сложнее становится и обработка сигнала из-за резкого возрастания тока теплового излучения /Тф, см. § 4.5, 4.6 (подробнее возможные ограничения из-за /Тф будут рассмотрены ниже при анализе ДТ’пор реальных тепловизоров). Все сказанное объясняет, почему в тепловизорах находят применение ФП на диапазоны как 8 ... 24 мкм, так и 2 ... 5 мкм.
Зависимость ДГрад от температуры фона. Зависимость Д71рад(71) отличается от зависимости Рра1{Т), так как коэффициент 0, связывающий эти величины, сам является температурно-зависимым 0^2£Г2. Используя методику § 1.2, аппроксимируем сначала квадратичную зависимость экспонен
Циальной:
|
АТ'рад*7’) 6 (Г) £>;ад(Г) |
![]() Используя эту заготовку, а также (3.119), (5.42), получаем искомую температурную зависимость: -• .. ,
Используя эту заготовку, а также (3.119), (5.42), получаем искомую температурную зависимость: -• .. ,
Гр(2^)ехр(-!^
АТ'^Т,) ■ 6(Г.) о;ад<г„)
= ехр!'Д7 (5.69)
Где коэффициент
____ 5,2 Ь£ ■ I 2 Ъс, 1-А (5.70)
& ~ 2 — 2кТгХ1' 2ЬТ2Н' ^ Т
При Х” = Ь мкм = 5-10-4 см, Т — 293 К
___ 6.62' 10~34--3- 10го __ 9 о//К. V (5.71)
Ь г-ЬЗв-КН^ЭЗ^-З-К)-* ‘ 293 '* '
Г при Х1'--^ 14 мкм^= 1,4* 10-3 см
А' = _ 6,62-10-34-3- Ю1р Ь5------ 0 у' % /К_ (5.72)
Ь 2> 1,38 • 10-еа (293>2-1.4-10-* " 293 ~ у
Коэффициент отрицателен. Значит, с повышением температуры чувствительность тепловизора улучшается и тем сильнее, чем меньше X" (при X"^.кс2/,ЪкТ2). Численное значение!" (в приведенных формулах оно выражено в процентах) показывает, насколько снижается А^рад ПРЙ повышении температуры фона на один градус. Абсолютный предел чувствительности ~1/уТ. Это соответствует следующему процешному изменению тт ДГрат на каждый градус фона: , , :-
Ттд Тпл,(Т)______________________ ъГт* т/ Тп / Д Т
. 7^Ф'~УГТГ 1' Л+Д7-~еХР1 2Г
£'= —1/2Г« — 1/(2-293)«—0,15% К. (5.73)
Для разработчиков ФПУ улучшение температурной чувствительности при повышении температуры фона является своего рода «тепловизионным парадоксом». Они привыкли, что параметры ФПУ ухудшаются с ростом Т: увеличиваются фоновый ток и шумы, переполняется накопитель ячейки матриц. Улучшение чувствительности тепловизора с ростом Т объясняется тем, что тепловое излучение является для тепловизора не помехой, а сигналом — точнее, сигналом является приращение числа квантов при нагреве тела на 1 К, а это приращение тем выше, чем выше температуры тела.
Пороговая разность температур тепловизора с реальными ФПУ. Основная сложность расчета ДГп0Р для реальных ФП — в зависимости квантового выхода от длины волны л (М* ^3_за этого при точном расчете Агэф приходится проводить численное интегрирование плотности фотоактивных пар г| (А,) я (Я). Однако в § 1.2 было показано, что такого численного интегрирования можно избежать и определять Аф реального ФП (с типовой спектральной характеристикой, подобной кривой 3 на рис. 1.7) по аналитическим формулам для идеального ФП (1.34) — (1.36). Поскольку и коэффициент“!}? и £>рад(Я") определяются через значение А^Эф, то при расчете Д7"поР также можно избежать указанных осложнений. Методика расчета Д7*ор оказывается следующей.
1, По относительной спектральной характеристике реального ФП находят коротковолновую X' и длинноволновую X” границы чувствительности (по уровню 0,5 от максимума). Затем
С помощью аналитических формул для идеального ФП (1.34)__
(1.36) рассчитывают значение А/эф(Я', }").
2. Далее следует рассчитать удельную обнаружительную способность. Для ФПУ принято определять этот параметр в максимуме чувствительности Однако в теплови-
Зионное соотношение формально введена величина Орад(А,"), Хт < А". Поэтому в соотношение (5.63) следует подставить £радМ^(^УАт)£рад(^т)> а значение £>рад (Ят) рассчитать по следующей формуле:
(>•*)=К/Ьс У'гл'эф (V. п - (5-74)
3. Методика расчета в сохраняется прежней: для этого коэффициента можно либо принять усредненное значение (5.61), либо найти его более точное значение по (5.60) или с помощью рис. 5.2,6.
4. Потери в чувствительности. ФПУ, дополнительные шумы " приводят, естественно, к снижению отношения А^с/ш на выходе
ФПУ (при постоянном входном сигнале). Во сколько раз ухудшилось отношение Лгс/ш, во столько раз ухудшилась и об - наружительная способность ФПУ О*, и пороговая разность температур тепловизора Д^*ор • Однако для обнаружительной способности «ухудшение» означает уменьшение ее численного значения, а для пороговой разности температур ухудшение — это повышение ее численного значения. Прямо пропорциональная зависимость между О и А^/ш и обратно пропорциональная между ДТпор и Агс/ш вытекают непосредственно из определений этих параметров (3.112), (3.113),
(5.53):
О ^с/щ/'Еса, ДТПор = АТУ^с/ш. (5.75)
Таким образом, если обнаружительная способность О* реального ФПУ будет хуже, чем в идеальном, в £>£ад/£)* раз, то пороговая разность температур ДГ„ор тепловизора на основе такого ФПУ станет хуже (возрастет) в те же £>£ад/£)* раз:
Т* _лг* ^рад (^/я) __________ п к" _ ГУ* п ч ^рад
Пор Д/ рад д* ^ 0 ^ ККт) ^ —
Удельное значение ДПор зависит от способности каждого,• отдельного канала ФПУ обнаруживать слабые сигналы. В предыдущих параграфах было отмечено, что удельное значение
|
21МЬАЬ у Т] У'тклзэг) * (5.77) Ничего неожиданного для нас в этом выражении нет: вновь встретились с произведением ТкЛ4эг], которое определяет обна- ружительные свойства матриц (см. § 4.6). Чтобы получить малые значения ДГпор, произведение гТкМэ должно быть максимальным. А это значит, что матричное ФПУ должно обеспечивать идеальное пространственно-временное накопление: без потерь фотонов (т) = 1), в течение всего времени кадра (Тн = = тк) и во всех точках кадра (МЭ = М). Так что формула (5.77) еще раз подтвердила наш тезис: чтобы наилучшим образом решить задачу, поставленную перед оптико-электронной системой, надо прежде всего оптимально обнаружить слабый оптический сигнал. Говоря спортивным языком, «индивидуальная техника» каждого отдельного элемента ФПУ нас устраивает — элемент справляется со своей задачей оптимального обнаружения слабого оптического сигнала, удельные значения Д7*0р реальных и идеальных тепловизоров близки. Однако «командная игра» ФПУ оставляет пока желать лучшего. В § 4.6 было показано, что одновременно обеспечить все условия (Т1 = 1> ТК~ТП, МЭ = Л4) не удается, поэтому АТиор реальных тепловизоров ху- |
|
-тг/: |
|
~м—■ во |
|
Рад |
|
00 |
|
|
 |
Же, чем идеальных (при использовании идеализированной матрицы). Принципиальные ограничения здесь связаны с большим фоновым током. Если в матричном ФПУ и во внешних устройствах из-за большого фонового тока /0 не удается обеспечить накопление в течение всего времени кадра и если время накопления Тн будет ограничено емкостью накопителя (его максимальным зарядом фтах=/07н) то согласно (5.77), (3.112)
|
|
||
|
|||
Как видим, при такой неоптимальной обработке сигнала переход в более коротковолновый диапазон становится даже выгодным [116].
|
, 2-10-'.. 1.77. №■ У 2.0.04-2,5.10-» °’03 |
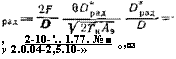 Проведем численную оценку значений Д7'ПОр для двух типичных примеров: при использовании матрицы ПЗС на основе барьеров Шотки (спектральный диапазон 3 ... 5 мкм) и при использовании одноэлементного ФД на основе КРТ (8,.. 12 мкм). Удельная радиационная обнаружительная способность этих приборов составляет соответственно 1,77 • 1011 и 5,81 ‘101а (табл. 3.3). Пусть относительное отверстие DF = : 2, размер элемента l~YA3=5Q мкм, Лэ=2,5-10~5 см2, формат кадра 300X400= 1,2-105, время кадра телевизионное Тк = 0,04 с. Тогда для матрицы на основе барьеров Шотки при Мэ = М, г)« 10"3, D*/D уЧ|« 0,03, получим
Проведем численную оценку значений Д7'ПОр для двух типичных примеров: при использовании матрицы ПЗС на основе барьеров Шотки (спектральный диапазон 3 ... 5 мкм) и при использовании одноэлементного ФД на основе КРТ (8,.. 12 мкм). Удельная радиационная обнаружительная способность этих приборов составляет соответственно 1,77 • 1011 и 5,81 ‘101а (табл. 3.3). Пусть относительное отверстие DF = : 2, размер элемента l~YA3=5Q мкм, Лэ=2,5-10~5 см2, формат кадра 300X400= 1,2-105, время кадра телевизионное Тк = 0,04 с. Тогда для матрицы на основе барьеров Шотки при Мэ = М, г)« 10"3, D*/D уЧ|« 0,03, получим
|
Для одноэлементного ФД на основе КРТ при г)«1
|
Большое число элементов матрицы на основе барьеров Шотки не только компенсирует низкий квантовый выход и более высокое значение £>*ад , но и обеспечивает лучшую температурную чувствительность. Она в три-четыре раза выше, чем ПРИ использовании одноэлементного ФД. Впрочем, достаточно применить КРТ ФД с числом элементов (3...4)2«10, чтобы достичь той же расчетной чувствительности, что и у рассмотрен
ной выше матрицы на основе барьеров Шотки формата 300Х Х400.
Полученные численные значения чувствительности — сотые, десятые градуса — типовые для современных качественных тепловизоров. Интересно, что абсолютный предел чувствительности при приведенных выше значениях D:F = 1:2, Аэ = 2,5*
• 10~5 см2, 7^ = 0,04 с, Т = 293 К составляет
„.„ат Р» , 7.3..0-» (5.81)
V D У2ТкА9 У 2-0,04-2,5- К)“5
Рассмотренные выше примеры показали, почему абсолютный предел не достигнут: при = l не удается обеспечить
ТК = ТК, а при ТН=ТК получаем ^<1- Так что две десятитысячных градуса — это еще не реализованный, да и не востребованный в ИК-технике предел температурной чувствительности теп - ловизиров.
Подведем итог. На примере тепловизора доказан тезис «чтобы лучше решить задачу, поставленную перед оптико-электронной системой, надо тгрежде всего оптимально обнаружить слабый оптический сигнал». Перед ‘тепловизором поставлена задача регистрации минимальной пороговой раз- лости температур АТП0р. Идеально решает эту задачу матричное ФПУ — оптимальный обнаружитель, обеспечивающий идеальное пространственно-временное накопление сигнала в течение всего времени кадра и по всей площади кадра (без сканирования). Качество тепловизора характеризуют удельной пороговой разностью температур ДТ’пор (рассчитанной для тепловизора с единичной полосой пропускания, с единичной площадью ФЧЭ, при условном относительном отверстии D F — 2:1). Для расчета А7^ор идеального тепловизора надо удельную обнаружительную способность ФПУ просто умножить на коэффициент 2kT1 (при более точных расчетах следует учесть незначительное— на 30%—снижение этого коэффициента с изменением длинноволновой границы от 0 до 14 мкм).
Температурная чувствительность идеального тепловизора улучшается с расширением спектрального диапазона и достигает абсолютного предела (минимального значения), когда ФПУ регистрирует практически все тепловые фотоны. Абсолютный предел зависит от температуры фона Т (уменьшается col Vf) и составляет 7,3-10-8 К-см-с|/2 (удельное значение при Г—293 К). С учетом типовых параметров тепловизора это соответствует •чувствительности 2-10~4 К.
В реальных ФПУ с длинноволновой границей 10... 14 мкм проигрыш в числе регистрируемых тепловых фотонов несуществен: потери в температурной чувствительности из-за ограничения спектрального диапазона составляют всего 12... 35 %. Принципиальными оказываются ограничения из-за недостаточной емкости ячейки матрицы, что приводит к потерям в накоплении и снижению АТВОр реальных тепловизоров примерно на два-три порядка (относительно абсолютного предела). Но даже при таких ограничениях современные тепловизоры обладают высокой температурной чувствительностью
0, 01 ...0,1 К.