Фотоприемные устройства и ПЗС. Обнаружение сла­бых оптических сигналов

Обнаружение слабых оптических сигналов в оптико-электронных системах различного назначения ИЗМЕРЕНИЕ МОМЕНТА ПРИХОДА ОПТИЧЕСКОГО ИМПУЛЬСА

Основы теории обнаружения слабых оптических сигналов необходимо знать разработчикам не только таких оптико-элек­тронных систем, которые лишь обнаруживают оптические сиг­налы. Знать эту теории необходимо яри проектировании прак­тически любой оптико-электронной системы: дальномеров (в которых требуется не только зарегистрировать сигнал, но и измерить момент его прихода), ВОСП (регистрирующих не •одиночные импульсы, а их последовательность), тепловизоров {различающих разность температур нагретых тел). Какую бы функцию ни выполняла оптико-электронная система, прежде всего надо обнаружить слабые оптические сигналы на фоне Шумов. Чем лучше справимся с этой задачей и получим боль­шее отношение сигнал-шум, тем лучше решим и основную за­дачу, поставленную перед системой: в ВОСП обеспечим прием информации с меньшими ошибками, в дальномерах повысим дальность и точность измерений, в тепловизорах зарегистрируем меньшую разность температур ЛТ.

Некоторые особенности обнаружения в ВОСП (широкопо­лосное усиление, необходимые режимы работы ЛФД), а также в теплопеленгаторах (использование многоэлементных ФПУ) рассматривались в предыдущей главе. Дополним это рассмот­рение еще двумя важными примерами — проанализируем роль оптимального обнаружителя в системах измерения момента прихода сигнала (§ 5.1) ив тепловизорах (§ 5.2).

Схема измерителя момента прихода сигнала. В ряде опти­ко-электронных систем — дальномерах, теплопеленгаторах на основе линейных ФП, рефлектометрах (определяющих по от­ражению в волоконно-оптической линии ее повреждение) —не­обходимо измерять момент прихода сигнала. Часто для реше­ния этой задачи используют обычную схему обнаружителя и момент прихода определяют по моменту срабатывания поро­гового устройства. При малом сигнале (когда амплитуда сопо­ставима с уровнем порога С/пор) срабатывание происходит в окрестности максимума выходного сигнала?«/м, а при боль­шом — в момент прихода сигнала. Поэтому погрешность поряд­ка времени нарастания фронта, так что при колоколообразном сигнале она не менее длительности оптического сигнала Тс (при широкополосном усилителе).

Чтобы повысить точность измерения, надо фиксировать по­ложение какой-нибудь одной, характерной точки выходного им­пульса. Очевидно, что такая характерная точка — это максимум импульса (? = ^м, рис. 5.1,а). Форму импульсного сигнала и время задержки системы считаем известными, что позволяет по моменту реконструировать положение входного оптиче­ского импульса (рис. 5.1,а). В максимуме производная равна нулю, следовательно, надо сначала найти производную сигнала, а затем момент времени, когда она становится равной нулю (рис. 5.1, б).

Согласно изложенному алгоритму изменяем схему обнару­жителя (см. § 3.1) следующим образом: между усилителем и решающим устройством включаем дифференцирующий каскад; в качестве решающего выбираем устройство сравнения с уров­нем и — 0 (в обнаружителе применялось пороговое устройство с порогом срабатывания 1/ПоР«3. ..6 0Ш, см. § 3.1). Так при­ходим к схеме рис. 5.1, г. Пока схема пригодна только для теоретика: она позволяет проанализировать сигнал и шум, рас­считать погрешность измерения /м, так что ее и будем исполь­зовать в этом параграфе. Однако схема на рис. 5.1,г непригод­на для практика: в ней регистрируются положения максимумов не только сигнала, но и всех шумовых выбросов. Поэтому сле­дует еще ввести нелинейные блоки селекции. Между усилитель­ным и дифференцирующим каскадами можно подключить ограничитель с уровнем ограничения и пор, тогда шумовые им-

Пульсы с амплитудой ниже 11пар не будут доходить до диффе­ренцирующего каскада. Можно совместить схемы двух устройств — измерителя и обнаружителя. Пороговое устройство выдает сигнал при £/^£/поР, а устройство сравнения при £/=0. Вырабатываемые этими устройствами сигналы должны иметь Длительность около Тс. Решение о наличии сигнала и о положе­нии его максимума принимает дополнительная логическая схе - Ма И (когда на ее вход поступают одновременно оба сигнала).

Конечно, «шальной» шумовой импульс большой амплитуды приведет к срабатыванию и в этих двух схемах. Но такая ложная тревога неизбежна, ее частота регулируется уровнем ^пор так же, как в обычном обнаружителе (см. § 3.1).

Погрешность измерения момента прихода сигнала. Шум, на- "кладываясь на сигнал, смещает его, что приводит к погрешно­сти при измерении момента tu - Расчет погрешности становится особенно наглядным, если считать реализацию шума иш(() в окрестности tM почти постоянной, как это изображено на рис. 5.1,6, в. Такое допущение физически обосновано:

Усилительный каскад 1 с эффективной постоянной тэ оди­наковым образом затягивает и сигнальный, и шумовой импуль­сы, поэтому их длительности Г05 и тш одного порядка (если Тэ>ТС), см. § 2,2, 4.1;

Время корреляции ткор совпадает с длительностью шумового импульса (§ 2.2);

Т05» тэ и ткор одного порядка;

Интервал в окрестности tM, в пределах которого смещается точка U = 0 (рис. 5.1,6), мал по сравнению с Tos, следовательно, этот интервал мал и по сравнению с тКор.

При широкополосном усилении Тш И Ткор, вообще говоря, меньше Т05~ТС> но интересующий нас интервал в окрестности tм еще меньше.

Поскольку шум смещает сигнал на малую величину, то точка пересечения перемещается по оси времени от максимума J = fM на следующую величину Д/м (рис. 5.1,6):

Uc'(tH)AtK=Ua{tH). (5.1)

Выборка шума иш (/м) — величина случайная. Поэтому, усредняя по всем вероятным знАченИям находим среднеквадратич­

Ную погредгаость V Д*мз (среднеквадратичное смещение точки

= 0) [S8J:

[C/.'(<m)J2Д»=ЬI(<J=wL /Кй=£/ш/1/с'(*«)- (5.2)

Ход дальнейших расчетов стандартен. Пусть k — частотная характеристика усилительного каскада 1, k% — частотная ха­рактеристика дифференцирующего каскада 2; — частот­

Ная характеристика всего измерительного усилителя (рис. 5.1,г). Соответственно будем обозначать Ulc, Um— СИГ' нал и шум на выходе усилительного каскада 1, а t/c, Um — на выходе всего измерительного усилителя. Сигнал и шум на вы­ходе усилителя с произвольной частотной характеристикой рас­считывались в § 3.2:

Uс (О = SEcKuc (^м); #с(£м) =

00 . ^ '

= 2Т'С ^ kez cos (to/M -{- фу) df > (5.3)

о

Соответственно значения £/1с(£м), £/11И рассчитаем при замене в этих формулах *

Для определения погрешности ]/КВ (5.2) надо научиться ассчитывать производную от сигнала. Выделим одну гармонику оэсоэ (со£-(-1|эс + ,Фу) и возьмем от нее производную:

ЧЇ 4ї ^ И + 'Фс-ИуН—« 5ІП (СО і + фс + фу) =

= СО СОБ (оуі -|— 1|5С Ч - ^|)у -}-л/2).

Как видим, дифференцирование гармоники равносильно умно­жению на круговую частоту « и сдвигу на фазовый угол я/2. Используя это правило, находим производную сигнала (5.3):

О'с/(4)=5Яса«с/(^м);

Оо

^с(^м) = 2ГС ^ к есы со5 (оз^м Ч-*Фс + *Фу - Ня/2) 4/•

Теперь надо (5.4) и (5.6) подставить в (5.2), и выражение для

У М м2 найдено:

ВкЧ/

(5.7)

X

2ТС сое +Фс + % +л/2) <//

О

Это самое общее представление формулы для У^Д^2. Ей можно пользоваться при произвольной структуре измерителя с произ­вольной частотной характеристикой &(/). Полезно конкретизи­ровать эту формулу, используя те сведения, которые нам изве­стны о схеме измерителя. Прежде всего нам известно, что вто­рой каскад — дифференцирующий. Это позволяет выразить па­раметры сигнала и шума на выходе измерителя через парамет­ры сигнала и шума на выходе усилительного каскада 1:

Цс(/)=**;,(/), ^'(0=^(0;

^сій^ЗЕсАІІс {£)> и С (4{) ~ (^м)*

&2—&--.і,±у.

24—4649

С помощью этих заготовок преобразуем (5.2) к следующе­му виду:

______ 1/ ~ ю2А|8е^

Л/~ Д 4- 2 _ V_______________ 2^/Щ ^ Ь

5£сА ц;с(/м) 5£са“1с(^м) ^ И[с (^м) ^

О

Первый и третий множители правой части полученной фор­мулы в комментариях не нуждаются. Первый множитель

У 2?/ш?*,в^//5ЯсАк1<.(<„)=1/ЛГс/щ (5.10)

О

Представляет собой отношение шума к сигналу; оно встреча­лось нам едва ли не во всех параграфах. Третий множитель представляет собой характеристическую частоту — частоту по­ложительных шумовых выбросов. Этот параметр встречался реже (см. § 3.1, 4.1, (3.22), (4.90)):

1/1

^хар= 2я_/*хар> _/*хар“ —“------------------------------------------------- . (5.11)

(' А,2©<*/

О

При белом шуме /хар с точностью до коэффициенту равна эф­фективной полосе усилителя по сигналу /у. Это следует ш (4.39), (4.44), (4.47), (4.52):

1/ г/■*,■«// гг

/-= %—1/-

Б

-Уттг-'-Ут? ; ■ - ■<«•»

Новым для нас является только второй множитель в (5.9) — отношение И1С (/м)/и1С/у(^м). Это отношение также оценим для более конкретной, типовой ситуации, когда оптический импульс имеет стандартную колоколообразную форму, а усилительный каскад 1 — широкополосный. В этом случае выходной сигнал
и1С тоже колоколообразный, а в окрестности максимума его как правило, можно аппроксимировать косинус-квадратной функцией. Это видно на примере рис. 4.7, 4.9, 4.12 (полоса уси­лителя здесь сформирована оптимальным фильтром, а также фильтрами первого и второго порядка — на основе одного и двух /?С-звеньев соответственно). При косинус-квадратной ап­проксимации значение производной будет равно

Й2 (. . яд*

— (1+С05 т

___ ц1с(^м) { л /С 1о

---------- 2------ <5ЛЗ>

Если Вы убедились, что в Вашем случае косинус-квадратная аппроксимация выходного сигнала в окрестности *ы справедлива,

То погрешность |/ Д^2 можно рассчитать по следующей форму­ле, вытекающей из (5.9) ~ (5.13):

“- = 4 (гг! (5Л4>

Каждое из полученных выражений для расчета У А^мг (5.7), (5.14) занимает свою «экологическую нишу». Обобщен­ное выражение (5.7) будет использовано для решения задачи, возникающей при разработке любой системы — при поиске пре­дельных значений параметров (максимальной точности изме­рения £м). В выражении (5.14) проявляются уже физические «очертания», в него вошли хорошо известные нам параметры теории обнаружения №1С/Ш, Т05, /хар. Эту формулу удобно ис­пользовать при анализе источников ошибок реальных измери­телей положения максимума сигнала.

Оптимальный измеритель. Найдем частотную характеристи­ку оптимального измерителя £(/) по критерию минимума по­грешности У На первый взгляд поиск экстремума (5.7) представляется сложной задачей. Однако и здесь нам помогает теория обнаружения. Оказывается, экстремум подобного выра­жения уже находили — это экстремум отношения сигнал-шум (см. § 3.2). Запишем отношение сигнала (5.3) к шуму (5.4) на выходе усилителя

Со

Кгес сое ((*>гм + Фс + й/

У%: — тгг~— (5Л5>

1/ [ вk^sdf

" о

Для удобства дальнейшего анализа здесь приведена замена

• Экстремум выражений (5.15), (5.7) достигается при следу, ющей фазочастотной характеристике усилителя: оптимальный обнаружитель

®^м4_‘фсН-,'фу==0, 1])у=в------ со/м--- Фс1 (5-16)

Оптимальный измеритель

Ф^м~Ьфс_{""фу-1-я/2=0, фу"—(о^м’—Фс я/2. (5.17)

При такой фазе (5.15) и (5.7) принимают соответственно

Вид

5£сД2Гс (

Мс, ш=У5^

1/1 вк^1/

'О

УГД<М»=^“------------------------------------------------------------------------------- . (5.19)

Мы убеждаемся, что формулы для ЛГт/ш И / Д V представ­ляют собой отношение идентичных интегралов, только в формулу ДЛЯ У Д*м2 вместо спектра ес входит спектр (йес (то, что числитель и знаменатель в (5.18) и (5.19) поменялись места­ми, при поиске экстремума никакого значения не имеет).

В § 3.2 было показано, что экстремум (максимум) отношения

■Мюлп достигается при оптимальной частотной характеристике

Й1 = ес/е. __ (5.20)

Поскольку в формуле для |/~Д*м2 «роль» спектра сигнала играет £сы, то, заменив ес-+есы, получим

Ь = ~ы = кхк 2. (5.21)

Подставляя (5.20) в (5.18), приходим к уже известному вы­ражению для отношения сигнал-шум оптимального обнаружи­теля:

5£сд27-с | («с/®)М/

Л^1с/ш = г^#=£----- 5-------------------- ■

(•: У2д1т

СО

I &(ес‘

А подставляя (5.21) в (5.19), находим минимальную ошибку оптимального измерителя: }

___ „ J, .702)адгсг/

Ущ~ ^2?/ш ° 1Л2?/

Г (есС0/в) (шес) £//

X

®2(^сг/в)^/ 5ЯсА2Гс / |(еса/в)й/

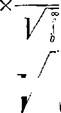
Первый множитель правой части (5.23)— это отношение сигнал-шум (точнее, его обратное значение) на выходе опти­мального фильтра (5.22), а второй — характеристическая ча­стота этого фильтра (тоже обратное значение), сравните с.(5.11):

Г (ес2/е)4/ / I в(ес/0)2^/

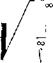
Поэтому для минимально достижимой ошибки идеального об­наружителя получаем следующую окончательную формулу [88]:

1

^1°с/ш®хаР

Формулы (5.21) и (5.25) являются кульминацией параграфа и подтверждают провозглашенные в начале главы положения.

1. Для решения задачи оптимального измере­ния 1М (с минимальной погрешностью) надо прежде всего решить задачу обнаружения. По­этому в состав оптимального измерителя должен входить опти­мальный фильтр (первый множитель к1 = ес1& в (5.21)). На его выход должен быть включен дифференцирующий каскад.(второй множитель к2~ы в (5.21)). Формула (5.21) доказала, что мы не ошиблись в выборе структурной схемы измерителя (рис. 5.1, г) и что такая схема будет оптимальной, если в ка*

Честве усилительного каскада 1 выбрать оптимальный фильтр.

На практике часто используют комплексную форму коэф­фициента передачи К (со). Комплексный коэффициент передачи оптимального фильтра К1 задавался (3.47). Фазовый сдвиг дифференцирующим каскадом на л/2 (5.16), (5.17) соответ­ствует умножению на мнимую единицу. Поэтому

К1 = ехр(—}Ым)ес*/&, К2=/о),

=/со ехр(—}(о(м)ес*/&. (5.26)

2, Чем лучше мы справились с задачей обна­ружения — получили большее отношение си­гнал-шум, тем лучше мы решили и основную за­дачу — измерили t. ж с меньшей погрешностью. Это положение справедливо как для оптимального измерителя, так и для квазиоптимального (Во всЯком случае, при белом шуме): согласно (5.14) и (5.25) У Д^м3 00 1/А^с/ш-

Рассчитаем минимальную погрешность у Д*м2 для двух стан­дартных случаев: преобладание белой либо ВЧ-составляющих шума.

Белый шум. Расчет У^Д^,2 согласно (5.25) сводится к расче­ту характеристической частоты. Полагая 0=1, к^ — вс при спектре колоколообразного сигнала (2.14), получаем

Г о)2 эт2соГс^/

3

<огГсЧ1~(<»Гс/п)Т

СО

I* эт2 соГей'/

3 "со2ГсЧ1-(<оГс/д)Т

(5-27)

Таким образом, минимальная погдещдость намерений согласно

(5.25) и (5.27) равна ;

Л ^с/ш *.81ЛГ1С/Ш*

Как видим, теоретически можно различить смещение им­пульса примерно на (2Л'Т1С/Ш)—часть его длительности. При предельно слабых сигналах имеем Л^с/ш^6 ... 12 (см. § 3.1), поэтому такое смещение около 0,05... 0,1 Тс. Так что точность

В оптимальном измерителе повышается даже при столь слабых сигналах примерно на порядок (по сравнению с методом § 4 2) Высокочастотный шум. Теперь характеристическую часто­ту (5.24) следует рассчитать при 0= 1-Ь<оЕ/<ов2:

V ^4'

TOC o "1-5" h z

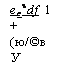№« Я

О О

Г

/ <0в*есЧ/ Г а*— г

У т~т; (5-29)

.Н-И/7Л.)а Г

1+(///в

Здесь при расчете интегралов учли, что ВЧ-шум преобладает практически во всей полосе сигнала,

После подстановки характеристической частоты (5.29) в

(5.25) получим

/Щ=1/^/1,22Лг1с, ш; т,= 1/0)»=1/2я/о. (5.30)

Сопоставляя (5.28) и (5.30), вИдим, что при ВЧ-шуме средне­квадратичная погрешность Удс2 значительно (примерно в 1,5 УхВ/Гс раз) больше, чем при белом шуме, даже если

Обеспечивается одинаковое отношение Л^с/ш. Это связано с тем, что при ВЧ-шуме полоса оптимального фильтра узкая (она порядка /в)> и поэтому выходной сигнал сильно затяги­вается (его длительность 1,4тВ) см. § 3.6).

Квазиоптимальный измеритель. Схема измерителя отличает­ся от схемы обнаружителя дополнительным дифференцирую­щим каскадом с частотной характеристикой 6 — /со. Синтез та­кого каскада не представляет труда: это дифференцирующий

Однозвенный фильтр с большой постоянной времени. Вся слож­ность заключается в синтезе первого каскада с оптимальной характеристикой ес/©. И вновь нас выручает теория обнаруже­ния. В § 4.1 были описаны принципы построения квазиопти - мальных обнаружителей, практически не уступающих оптималь­ным в отношении А'к/ш. Это дает нам полное основание исполь­зовать те же принципы и при разработке квазиоптимальных измерителей.

Однако методику синтеза квазиоптимальных фильтров нель­зя механически перенести на разработку квазиоптимальных из­мерителей. Возникают дополнительные ограничения, что следу­ет из выражения для среднеквадратичной ошибки (5.14). Три

Сомножителя в этом выражении — это три источника ошибок. Первый сомножитель обратно пропорционален отношению Лг1с/Ш. Параметры квазиоптимального фильтра (постоянные вре­мени Хф его звеньев) подбираются так, чтобы обеспечить мак­симум N]с/щ. Нас это полностью устраивает: чем меньше шум тем меньше он смещает сигнал Uc(t) (вспомните рис. 5.1,6) и, следовательно, меньше ошибка Д/м.

Второй сомножитель {Т05/Тсу показывает, что погрешность измерения возрастает из-за расширения выходного сигнала. Это тоже понятно из рис. 5.1, а, б: кривая Uc(t) становится бо­лее пологой, что приводит к более сильному смещению Д? м. Эффективные полосы оптимального и квазиоптимального филь - тров по сигналу /у практически совпадают, так что эти фильтры одинаково (почти одинаково) затягивают сигнал (особенности случая ВЧ'Шумов оговариваются ниже).

Специфика синтеза измерителя связана с третьим сомножи­телем. Чем больше характеристическая частота /хар по отноше­нию к полосе сигнала fc = /2Tc, тем больше погрешность изме­рений. Согласно определению (5.11) большое отношение /хар//с свидетельствует о заметном ВЧ-шуме. На рис. 5.1,6, в реализа­ция шума принималась почти постоянной в окрестности /м. Но при наличии в спектре шума ВЧ-частот реализация Um(t) изме­няется быстрее, даже в малой окрестности /м наблюдаются шу­мовые выбросы (fxap — это и есть частота положительных шу­мовых выбросов). Шумовые выбросы, накладываясь на пологий максимум сигнала Uz(t), могут «просочиться» на вход диффе­ренцирующего каскада. Измеритель ошибется — измерит, по­ложение максимума не только сигнала, но и шумового выброса.

При синтезе квазиоптимального фильтра (см. § 4.1) число звеньев и его постоянные времени Тф выбирались без учета fxep. Если fxар возрастала на порядок (по сравнению с ее значе* нием в оптимальном фильтре), то предлагалось обеспечить заданную частоту ложной тревоги незначительным (на 4 ... ...20%) повышением порога срабатывания £/ПОр. Форму­ла (5.19) показывает, что в измерителе так легко «справиться» с /хаР не удается, недостаточно обеспечить максимум A'ic/ш, выбрав полосу квазиоптимального фильтра fy равной полосе оптимального. Как следует из определения fxap (5.11), необхо­димо еще обеспечить крутой спад (f) на высоких частотах />/у: при белом шуме £^1 /р, а при ВЧ-шуме

Белый шум. Однозвенный фильтр не обеспечивает необхо­димого высокочастотного спада. В этом фильтре k col If (при

F>fс) И fxap

(см. (4.91)). Поэтому в качестве квазиопти­мального в измерителе надо использовать фильтр более высо­кого порядка — двухзвенный с тэ = етф = Гс (см. § 4.1). Оценим

Потери точности V Ми2 измерителя на основе такого квазиоп­тимального фильтра, используя данные § 4.1.

Первый источник потерь — это потери в отношении ЛЛС/Ш_ Согласно (4.69)

П = (А/1С/ш)квази/^с/ш — 0>965. (5.31У

Второй источник потерь — это затягивание выходного им­пульса, которое в квазиоптимальном фильтре несколько боль­ше, чем в оптимальном (§ 3.6 (4.98)):

:(Го5 квази/Го5 opt)2 = (1,35ГС/1,28ГС)2 = 1,11. (5 щ

Третий источник потерь — в изменении характеристической частоты. Согласно (5.12) и табл. 4.1 для выбранногб квазиопти - мального фильтра /*ар равна

/харквази = /у f У ^~27Г "лГ* (5.33)'

Так что харкктеристическая частота увеличивалась по сравне­нию с ее значением в оптимальном фильтре (5.27):

Д., кврзи = (Л Ш (2 у 2 Т) = lЈЈ = {>5_ (5.34)

/хар opt Vя I с / я

Все указанные потери приводят к тому, что среднеквадра­тичная ошибка при использовании квазиоптимального двухзвен­ного фильтра увеличивается в следующее число раз:

(Т/дЩ. азн/а'АЩ)»р1«(1/0,965)-1,11-1,5= 1,7. (5.35)

Как видим» погрешность в основном возросла из-за боль­шой характеристической частоты.

Найдем теперь кривую настройки —зависимость Ул£м2 от эффективной ПОСТОЯННОЙ времени фильтра Тэ = еТф. Необходи­мые аппроксимации для зависимостей А^с/ш(тэ), Т0$(хэ) приво­дились в § 4.1 (см; (4.66), (4.30)). С их помощью получим

Ум и2 *1с/ш / Т 05 2 Л

(У Мы )квазк (^1с/щ)квазн l/'osKBaan } / у га

~У

Л[ (Гс/Тэ) +(тэ/71с) (Гс/тэ) + 0,81(гэ/Гс) (5 36)

У 2 1,81

Среднеквадратичная ошибка более критична к настройке фильтра, чем отношение ЛГ^/ш (ср. (4.66) и (5.36)). В узкопо­лосном фильтре (тэ^Гс) точность У дополнительно ухуд­шается из-за сильного расширения выходного сигнала, а в ши-

377

Рокополосном (тэ<Тс) — из-за увеличения частоты /хар.

Высокочастотный шум. При преобладании ВЧ-шума двуу - звенный фильтр оказывается непригодным:

*<N>1 в СОЇ2,

Поэтому интеграл (5.11) расходится, fxap_>'00. Как указывалось в § 4.1, для обеспечения конечного значения /кар нужен как ми­нимум трехзвенный 7?С-фильтр, Если согласовать эффективные полосы оптимального и трехзвенного фильтров, то можно до­биться достаточно близких значений /хар и Л^с/ш - Однако поте­ри в точности трехзвенного фильтра все равно будут сущест­венны из-за малой производной Это объясняется тем,

Что фазочастотные характеристики рассматриваемых фильтров различны, поэтому в трехзвенном фильтре выходной сигнал в области максимума пологий, в то время как в оптимальном он имеет ярко выраженный максимум, см. рис. 3.22 (аппрокси­мация (5.13) для оптимального фильтра при ВЧ-шуме не «про­водит»), Оказывается, выгоднее настроить трехзвенный фильтр не на полосу /в, а на полосу сигнала /с: падение Мс/ш перекры­вается увеличением и і/'(/м). Но и при такой настройке трех­звенный фильтр заметно уступает в точности оптимальному. Можно анализировать и более сложные структуры фильтров, но кардинальное решение — использование в измерительных устройствах ЛФД (см. § 4.2).

Подведем итог. В состав оптимального измерителя обязан входить оп* тимальный фильтр, обеспечивающий максимальное отношение сигнал-шум. Достаточно на выходе такого фильтра включить дифференцирующий кас­кад—-и схема оптимального измерителя (его линейного канала) синтезиро­вана. Дифференцирующий каскад формирует производную от выходного сигнала оптимального фильтра, последующая схема сравнения определяет ■момент, когда эта производная равна нулю—таков оптимальный алгоритм измерения максимума сигнала. Такой оптимальный измеритель при входном белом шуме способен различать смещение колоколообразного импульса при­мерно на 2А^с/ш — часть его длительности.

В реальных измерителях оптимальный фильтр при белом шуме можно заменить двухзвенным, настроив его на максимум отношения сигнал-шум, а дифференцирующий каскад выполнить на основе дифференцирующего /?С - звена с большой постоянной времени. Такой квазиолтимальный измеритель уступает в точности оптимальному примерно в 1,7 раз.