Фотоприемные устройства и ПЗС. Обнаружение сла­бых оптических сигналов

Обработка сигнала в реальных фотоприемных устройствах КВАЗИОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ

Теория обнаружения четко сформулировала задачу разра­ботчика фотоприемного устройства — максимизировать отноше­ние сигнал-шум. Для этого надо не только выбрать высокочув­ствительный фотоприемник, снизить шум, но и синтезировать схему усилителя с частотной характеристикой оптимального фильтра. При решении этой нелегкой задачи возникает ряд вопросов.

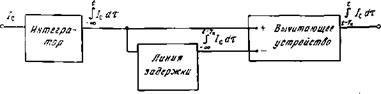
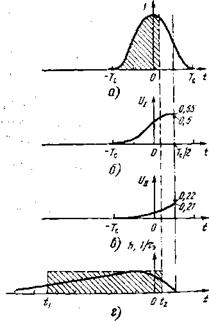
Вопрос первый. Как обеспечить заданную частотную харак­теристику усилителя? Прямая задача — расчет такой харак­теристики по известной схеме — тривиальна. Однако решения обратной задачи — методики синтеза схемы с произвольно за­данной частотной характеристикой — в общем виде не сущест­вует. Конечно, в частных случаях методом подбора удается син­тезировать схему с нужной характеристикой, Классическим при­мером является схема оптимального фильтра для обнаружения импульса прямоугольной формы при белом шуме (рис. 4.1) [4, 82], В § 3.5 было показано, что оптимальная схема в этом случае должна представлять собой интегратор с временем ин­тегрирования Гц = 7’с. Чтобы обеспечить накопление только на заданном интервале [/, 1.—Гн], сигнал с выхода интегратора раз­ветвляют на два канала. Во втором канале он проходит через линию задержки, а затем оба сигнала поступают на входы дифференциального усилителя. Последовательность линейных операторов этой схемы может меняться (интегратор стоять за дифференцирующим усилителем). В реализации даже такой простой на вид схемы встречаются затруднения: достаточно

Сложным компонентом является линия задержки; ограничена емкость интегратора.

К сложным и громоздким схемам приводят приближенные методики синтеза оптимальных фильтров для импульсов коло­кол ообразной формы [82].

Вопрос второй. Всегда ли реализуем заданный оптимальный

Фильтр? При белом шуме импульсная характеристика опти - ' мального фильтра должна повторять форму сигнала Л(Д*) —

= ес(А()!Тс (см-и§ 3.5). Если, например, сигнал симметричный

И прямоугольный, то и импульсная характеристика /г(Д*) сим­метричная и прямоугольная (рис. 4.2, а). Напомним, что

Д(д/)__ это отклик на дельта-

Импульс, Пришедший в момент

Т=^0 (рис. 4.2,6). Так что

Получается нереальная си - __ Е

Туация: отклик на выходе 1 ^ /-г

НЩ) появляется раньше, чем сигнал пришел на вход! Ясно, что фильтр с такой импуль­сной характеристикой не мо­жет существовать в природе.

Выход из положения есть: по­скольку аргумент импульсной характеристики оптимально­го фильтра определен с точ-

Рис. 4.2. Импульсные характеристики оптимального фильтра:

А — фнзот^ескк нереализуемая; б — входной дельтаобразяый импульс; е, г — реализуе­мые

Ностью до постоянной (произвольного времени задержки £зад (3.144)), то надо, перемещая импульс &(Д/) вправо по оси времени, совместить его начало с нулевым моментом времени Д/=0. Для рассматриваемого случая 4ад=^с/2, /і(Д£) =

&ес(Д/—0,5ТС)/ТС (рис. 4.2, е). Именно такую импульсную характеристику имеет рассмотренный оптимальный фильтр (рис. 4.1). Если в момент / = 0 на вход пришел дельтаобразный импульс, то в тот же момент на выходе интегратора возникает сигнал, пропорциональный заряду импульса. Через неинверти­рующий канал дифференциального усилителя этот сигнал пе­редается на выход. Только через время Тс через линию задерж­ки такой же сигнал поступает и на второй, инвертирующий вход дифференциального усилителя, который вычитает теперь два равных сигнала и дает на своем выходе ноль.

При симметричном импульсе произвольной формы ес(і) Указанная задержка /зад должна быть не менее половины дли­тельности сигнала по основанию. Для колоколообразного им­пульса /зад^^с (на рис. 4.2,г выбрано минимально возможное значение ізад, = Тс). Форма выходного сигнала рассчитывалась в & 3.5 как раз для фильтров с такими «сдвинутыми» характери­стиками (рис. 3.20 и 3.21).

А если функция ес(0 не имеет «начала» и асимптотически Стремится к нулю лишь при І-+-—ос? Такой случай встречает-

Ся в теории при учете дифракции в оптической системе, что приводит к размытию границы светового пятна. Это дает ос­нование аппроксимировать сигнал симметричной гауссовской зависимостью, непрерывно спадающей при Естествен­

Но, нельзя совместить несуществующее начало кривой Л(Д/) = = ес{{—(о)1Тс с моментом Д* = 0, импульсная характеристика к (Д/) всюду больше нуля, даже при Д^<0. А это уже физиче­ский абсурд: сигнал на выходе фильтра должен появиться рань­ше, чем он пришел на его вход. С подобной ситуацией также сталкиваемся, когда в спектре шума доминирует НЧ-либо ВЧ-составляюшая. В § 3.5 было показано, что и в этом случае импульсная характеристика устремляется к нулю только на бесконечности. Итак, получен однозначный ответ на постав­ленный вопрос: оптимальный фильтр не только трудно реали­зовать, но в ряде случаев он просто не может существовать в природе.

Вопрос третий. Нужен ли вообще оптимальный фильтр? Вопрос на первый взгляд кажется крамольным: ведь доказано, что максимум отношения сигнал-шум Мс/Ш обеспечивается при оптимальном фильтре. А если отношение А'гс/ш некритично к форме частотной характеристики к(1), значению полосы /у или, иначе говоря, добротность резонансной кривой #С/ш(/у) будет низкой? Тогда вопрос уже не кажется праздным. В этом слу­чае требования к настройке системы значительно упростятся, условие к($) =ес (/)/©(/) можно будет выполнять с весьма боль­шим допуском.

Вновь обратимся к классическому примеру белого шума 2^/щ и постоянной плотности сигнала 23ЕсаТс в полосе О... 1 /27’с (§ 3.3). При точной настройке, т. е. при выборе оп­тимальной полосы 1Уо?1=./2Тс, в § 3.3 получили

£/са = 23£сАГс/у ор^&ЕедГе (1/2Гс) =5£сА,

= у орі »

-/Vс/ш — иса/— 8ЕС/У2д1ш/у оре.

Выберем теперь полосу усилителя /у уже, чем у оптималь­ного фильтра:

Ис 23ЕС&Тс/у — 3Ес&/у//у орі,

II01 = У2дІшґу, т 5£са/у

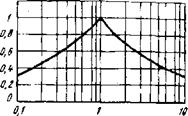
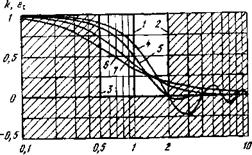
Формы частотной характеристики. Это поясняется рис. 4.4, где представлены частотные характеристики трех только что рас. смотренных ступенчатых фильтров с полосами fyopt; fу opt/2; 2/yopt (кривые 1—5). Наряду с ними изображены типовые ча­стотные характеристики и спектры, с которыми оперировали (или будем оперировать) : это спектры прямоугольного (4) и колоколообразного (5) сигналов, частотные характеристики простейших фильтров на основе ЯС-звеньев— при использова­нии одного (6) либо двух (7) таких звеньев. После весьма сильной (четырехкратной) вариации полосы рассмотренных ступенчатых фильтров (кривые 2, 3) различие в характеристи­ках и спектрах 4—7 кажется не очень серьезным. И если даже четырехкратное изменение полосы (кривые 2, 3) приводило к умеренному падению отношения Nc/m (в пределах 30%), то МОЖНО ожидать еще меньшего изменения суш ДЛЯ фильтров с более близкими частотными характеристиками 4—7. Отсюда можно сделать не один, а сразу два вывода:

Если вместо оптимального фильтра (например, с частотны­ми характеристиками 4, о) использовать фильтр с какой-либо другой характеристикой, близкой к оптимальной (например, 6, 7), то проигрыш в отношении Лгс/ш будет незначительным;

Само отношение Nc/m достаточно слабо зависит от мелких деталей формы сигнала, поскольку спектры таких сигналов близки (кривые 1, 4, 5).

Собственно говоря, последний вывод нам известен (см. § 3.3): отношение ЛГС/Щ для сигналов разной формы — прямо­угольной, косинусквадратной, вида (sоnx)/x — отличалось все­го на 15% (спектры этих сигналов на рис. 4.4 представлены КРИВЫМИ 1, 4, 5). ИмеННО НекрИТИЧНОСТЬ ОТНОШеНИЯ А'с/ш к мелким деталям формы сигнала и позволила применить в § 3.3 приближенную методику — заменить реальный спектр прямо­угольного импульса ступенчатым и получить при этом одина­ковые значения А'с/ш как при строгом расчете по точному

Спектру прямоугольного импульса, так и при приближенном расчете по ступенчатому спектру (табл. 3.2). Варьируя в § 3.3 подобным образом спектр, добивались изменения формы сигнала.

Итак, получен ответ на последний вопрос. Частотная харак­теристика реального обнаружителя может и не воспроизводить в точности частотную характеристику оптимального фильтра, ее можно выбирать достаточно произвольно — лишь бы харак­теристические частоты (эффективные полосы) реального и

Оптимального фильтров были близки [83, 84]. Поскольку такой реальный фильтр мало уступает оптимальному в отношении

Сигнал-шум, то его называют квазиоптимальным (почти опти­мальным) .

Трудно переоценить значение этого вывода для разработчи­ков систем обнаружения, в том числе и разработчиков ФПУ* Невозможно даже представить все трудности, с которыми бы сталкивались ЛРИ приеме сигналов в противном случае-—если бы отношение Л/с/ш резко зависело от настройки системы. \ дело не только в сложности реализации заданной оптималь­ной частотной характеристики. В принципе могут быть неста­бильными все параметры задачи: и самого оптического сигна­ла (так, из-за различной аберрации по полю оптической систе­мы может изменяться диаметр пятна и, следовательно, дли­тельность сигнала), и спектра шума (при вариации фонового излучения и температуры), и усилителя (например, из-за тем­пературной и временной нестабильности конденсаторов и рези­сторов фильтра). Все это при резком резонансе кривой ДО ш(/у) приводило бы к расстройке системы, к резкому сниже­нию отношения Л"С/ш. Возникла бы необходимость в разработке сложных адаптивных фильтров даже при относительно небольшой вариации параметров системы. К счастью, некритич - ность отношения АгС/ш к настройке фильтра позволяет избежать все эти трудности.

История развития техники обнаружения как в радиолока­ции, так и фотоприемных устройств оптических сигналов знает примеры, когда разработчики стремились обязательно воспро­извести частотную характеристику оптимального фильтра. Как правило, это приводило только к необоснованному усложнению системы, повышению стоимости, снижению надежности. Ухуд­шение эксплуатационных характеристик было неравноценной платой за несколько процентов выигрыша в отношении сигнал-шум (по сравнению с простой квазиоптимальной систе­мой). Впрочем, неоправданно сложная схемотехника зачастую вносила дополнительный шум, так что терялись и эти несколь­ко процентов выигрыша.

Особое значение приобретает квазиоптимальная фильтра­ция в многоканальных системах. Громоздкие оптимальные фильтры в каждом канале при их числе Ю2 ... 103 и тем более при 104... 10е были бы технически просто неосуществимы.

Таким образом вопрос: как построить оптимальный фильтр? заменен вопросом: как построить квазиоптимальный фильтр? Методика синтеза квазиоптимального фильтра в традиционных ФПУ очевидна: его надо формировать самым простым спосо­бом! В радиотехнике нет проще фильтров, чем /?С-звенья. Как правило, в ФПУ достаточно использовать одно-два таких зве - на '[85, 86]. Постоянную времени следует подбирать так, чтобы полосы пропускания такого ^С-фильтра и оптимального совпа­дали. При белом и ВЧ-шумах необходимо ограничить полосу пропускания фильтра сверху. Это обеспечивают интегрирующие ^С-звенья. Схема на рис. 4.5, а содержит одно интегрирующее звено. Два таких звена формируют более резкий спад частот­ной характеристики (рис. 4.5,6). При НЧ-шуме полосу надо граничить не только сверху, но и снизу, поэтому приходится применять всегда не менее двух звеньев (интегрирующее и

„____ T

О * о

В)

I

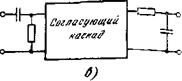
Рис. 4.5. Схематическое изображение квазиолтимальных фильтров:

А —с одним интегрирующим звеном; б — с двумя интегрирующими звеньями; д~ с дифференцирующим и интегрирующим звеньями

Дифференцирующее, рис. 4.5, в). Постоянные времени этих звеньев выбирают одинаковыми (если шум вида l/f наблю­дается во всей характеристической полосе сигнала fc= 1/2 7’,.). Примерами указанных квазиоптимальных фильтров мы в этом параграфе и ограничимся.

Порядок дальнейшего анализа очевиден: следует рассмот­реть прохождение сигнала и шума в таких фильтрах, выбрать постоянную #С-звеньев (полосу фильтров) так, чтобы отноше­ние Nc/m на выходе фильтров было максимальным; сопоста­вить это отношение со значением Мс/Ц10ф, которое достигается в оптимальном фильтре. Проведем этот анализ сначала для схем на рис. 4.5, а, б на основе интегрирующих /?С-звеньев, а затем для схемы на рис. 4.5, в, содержащей дифференцирующее звено.

Прохождение сигнала через однозвенный интегрирующий ^С-фильтр. Частотная характеристика такого фильтра соглас­но схеме рис. 4.5, а равна

^ (/) “ (W i®C) / { / j(oC--R) = /(--j&CR) —

= 1/.(1+>тф), тф=ЯС. (4.10)

Поскольку k(f) является спектром импульсной характеристи­ки, то последнюю можно найти с помощью обратного фурье- преобразования (3.142):

Сс

H. (Д*) = 2 f | k {f) | cos (шД*4-1£у) й?/--=(1/тф) exp ( Atjтф), (4.11)

0

— arctgon^.

Импульсную характеристику в данном случае можно было и не рассчитывать — экспоненциальный характер релаксации в системе с одной постоянной времени всем хорошо известен и является учебным примером переходного процесса.

Один из основных параметров фильтра-усилителя — его эф' фективная постоянная времени (или время наблюдения, эффек-

Л/т,

' ' г в)' * “/г'

Рис. 4.6. Импульсные характеристики фильтров с одним (а) н двумя (б) ин­тегрирующими звеньями

Тивное время накопления). В § 3.5 по аналогии с сигналом определен этот характеристический параметр как длительность эквивалентной прямоугольной импульсной характеристики Нэ. Заменим реальную импульсную характеристику однозвенного фильтра эквивалентной (рис. 4.6, а). Поскольку площади и амплитуды обеих характеристик равны

Оо

А, т,= §А(Д9<<Д<, К, = А(<„), <м=0, (4.12)

О

То для эффективной постоянной времени получаем следующее значение:

Со оо

5 А (ДО ■ли - $ £ ■Оф <(-I-Ц).«ЙИ ■- щу. (4.■ 1:3)

О о

Й(*м)^1/Тф, тэ= 1/А(^)--=Тф. (4.14)

Эффективная постоянная времени однозвенного фильтра оказывается в точности равной его ^С-постоянной. Соответ­ственно эффективная полоса частот рассматриваемого усили­теля есть? у = 1/2x9= 1/2тф (точно так же, как эффективная по­лоса частот сигнала была принята /С=1/2ГС).

Интересно, что тэ можно очень просто определить по макси­муму импульсной характеристики (4.14). Как будет показано позднее, эта формула носит общий характер — она справедли­ва для любого фильтра.

С помощью приведенной импульсной характеристики (4.11) найдем теперь выходной сигнал. При колоколообразном вход­ном сигнале, используя (3.138), получаем *

1гс(*)= и т)0с(т)<гт=

—оо ^

*

^ — ехр / — (/ — 1>/Тф] СОБ2 ^ с1х. ^4.16)

-г„

Г J

T/h

Uz А /

О

*)

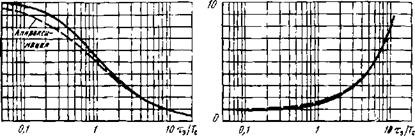
Рис. 4.8. Зависимости амплитуды (а) и длительности (б) сигнала на выходе однозвенного фильтра от его постоянной времени

Решение этой квадратуры очень громоздко, поэтому лучше обратиться к рис. 4.7, 4.8, на которых построены все нужные зависимости, рассчитанные по (4.15): это относительная форма выходного сигнала uc(t) и значения его основных парамет­ров— амплитуды мСА и длительности Г05 (по уровню 0,5 от амплитуды) при различных значениях постоянной времени RC-

ЦеПИ Тф.

При безынерционном фильтре сигнал не искажается:

Тф~0; Wca=Јca~1; Тйь=Тс. (4.16)

В противном случае при очень большой постоянной време­ни выходной сигнал uc{t) воспроизводит форму импульсной характеристики. И значение uc(t) пропорционально площади входного сигнала, которая при всА~1 равна есА7,с = 7с. Поэтому

Uz(t) = (eCATJh{t)^Tz^-exp (—*/Тф).

Тф

Амплитуда и длительность такого сигнала соответственно равны

ТФ>Гс; «сА = «с(0) = Гс/Хф; ис(Г05)/исА =

= ехр(—^05—Тф1п2. (4.18)

Полученные предельные выражения (4.16), (4.18) помогают найти аппроксимации для зависимостей «слСтф), ГоЛ^ф) во всем диапазоне изменения постоянной фильтра Тф. Сложим длитель­ности и обратные амплитуды (4.16), (4.18):

1/иса(тф) = 1 + тф/Тс= (Гс + Тф)/Гс; УсА = Т’с/(Тс-Ьтф)> (4.19)

То5=7’сЧ-,'СФ1п2- (4.20)

Эти формулы сконструированы так, что в пределе при гф->0 и Тф-^оо они, конечно, совпадают с ранее полученными (4.16), (4.18). Но совпадут ли они с реальными зависимостями йсаЫ)» ^ов(тф) в окрестности интересующих значений Тф«Тс —это уже дело удачи. К счастью, рис. 4.8 свидетель­ствует о такой удаче: погрешность аппроксимаций вполне приемлема (в пределах 10... 15%), так что формулы (4.19),

(4.20) можно эксплуатировать при последующих расчетах.

Аналогичным образом находится аппроксимация и для — момента положения выходного сигнала на оси времени. Вход­ной сигнал располагаем так, что он достигает максимума при?0=0. При безынерционном фильтре максимумы входного и вы­ходного сигналов совпадают, поэтому ^м = 0. При Тф->-оо наш фильтр можно рассматривать как интегратор, его выходной сигнал есть интеграл от входного сигнала и поэтому растет, пока есть сигнал на входе— до момента Тс - Следовательно, 1-я—Тс. Итак, при Тф=0 ... оо получаем диапазон изменения == 0 ... Тс. Это отражает аппроксимация:

Тф7с/(Тс+Тф). (4.21)

Ее погрешность также не превышает 15%.

Прохождение сигнала через двухзвенный интегрирующий ■^С-фильтр. Проследуем тем же маршрутом, что и ранее. По­скольку частотная характеристика каждого ^С-звена есть 14.10), то для двух таких последовательно включенных звеньев ее надо умножить саму на себя:

£([) = 1/(1-Ь;оугф)2; Хф=ЯС. (4.22)

Импульсная характеристика

Й(Л0=2--------- ——2------ = —5-ехр(—А*/1ф)—

«) I + М Хф тф

“ ехр Г" “ тф) !х^;

(4.23)

— 2 аг^ о)Тф.

Эта характеристика представлена на рис. 4.6, б. Своего макси­мального значения она достигает в момент Так как

Каждое звено запоминает входное воздействие в среднем время Тф, то два звена способны запомнить его в течение вре. мени 2тф — такова качественная оценка эффективной постоян­ной времени тэ (эффективного времени накопления) двухзвен­ного фильтра. Ее точное значение находится по ^известной методике: в результате замены реальной импульсной характе­ристики эквивалентной прямоугольной (рис. 4.6, б) либо с по­мощью (4.13):

Й(Д*м) = А(тф) = — Е'1; <а=1/А(Д^м) = ехф. (4.24)

'Сф

Как видим, точное значение етф несколько превышает прибли­женную оценку 2тф.

Выходной сигнал при колоколообразном входном импульсе рассчитывается по формуле

М*) = $ -^г^ехр{^--т)-Тф]/Гф}со82^-^-^т. (4.25)

Решение этой квадратуры еще более громоздко, чем при одном ^С-звене. Результаты численного расчета формы выходного сигнала, его амплитуды и длительности приведены на рис. 4.9, 4.10. При малой постоянной ЯС-звена Тф<сТС) когда сигнал проходит через фильтр без искажений, для амплитуды и дли-

Тельности сигнала остается справедливым выражение (4.16). При инерционном фильтре на его выходе теперь имеем следу­ющий сигнал:

1 «*♦

Т

Амплитудное значение достигается при 1м=Тф:

Тф» 7С) 11сА.~ис (тф)=гс/(етф).

Длительность по уровню 0,5 рассчитывается с помощью (4.26):

Ч»7'с Т0ь = У6тф = 2,45тф. (4.28)

Как ВИДИМ, Тоа несколько выше эффективной постоянной вре­мени фильтра т9=етф=:2>72 тф.

Аппроксимации для зависимостей ыса(тф), ^»(тф), ?и(тф) можно подобрать теперь следующим образом:

(4.29)

(4.30)

(4.31)

— (1 + Т С! У Т £ (4Тф)2) Хф.

Эти аппроксимации выбраны так, что при предельных значе­ниях постоянной фильтра Тф-^0, Тф-^оо они совпадают с пре­дельными формулами (4.16), (4.27), (4.28). Несложен ком­ментарий и к (4.31): каждое #С-звено при малой постоянной времени задерживает сигнал (положение его максимума) на время Тф (4.21); соответственно два звена — на время 2тф. При большой постоянной времени максимум смещается на время тф< Все это следует и из (4.31).

Аппроксимации согласно формулам (4.29) и (4.30) постро­ены на рис. 4.10. Эти аппроксимации практически неотличимы от точных кривых — отклонения лежат в пределах 1 ...3%.

Шум на выходе фильтра. Выражение для среднеквадратич­ного значения шума на выходе произвольного фильтра-усили­теля было приведено в § 3.2 (3.32)

(4.32)

Сейчас рассматриваем белую и высокочастотную компонен­ты шум а

-2д! шы^С23^е2ш^=2дIш-+-(2яСвхеш)2 /Ч

Подставляя эту спектральную плотность мощности входного шума в (4.32), для выходного шума получаем

Со

«Ш = ]/ 2?7ш|к2(/)сг/ + (2яС„1гш)21/2к2(/)й/. (4.34)

0

Как видим, расчет белой и высокочастотной составляющих шума во всей полосе усилителя сводится к расчету интегралоз в (4.34). Эти интегралы определяют шумовые полосы фильтра. Интересно сопоставить их с другими характеристическими ча­стотами фильтра. Поэтому прервем на время расчет выходного шума и проведем систематизацию указанных частот, определя­ющих прохождение сигнала и шума в усилителе.

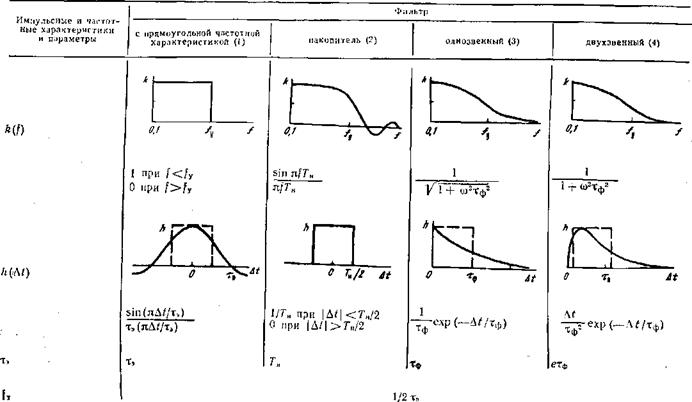
Характеристические частоты (полосы). В табл. 4.1 сведены импульсные и частотные характеристики четырех фильтров - усилителей: с прямоугольной частотной характеристикой

Накопителя (с прямоугольной импульсной характеристикой), одним и двумя /^С-звеньями. Таблица дополнена еще двумя фильтрами, которые уже фигурировали при анализе оптималь­ной фильтрации и к которым еще не раз будем обращаться в дальнейшем. Выбрано всего четыре примера фильтров с раз­ными частотными характеристика. Но и этих примеров до­статочно, чтобы проследить, как форма относительной частот­ной характеристики влияет на соотношение между характери­стическими частотами, ответственными за прохождение сигна­ла и шума через усилитель.

Эффективная постоянная времени и эффективная полоса фильтр-усилителя (по сигналу). Эти параметры характеризу­ют прохождение сигнала. В § 3.5 эффективная постоянная вре­мени Тэ^была определена как длительность прямоугольной им­пульсной характеристики Лэ(А0. эквивалентной реальной ха­рактеристике Н(а1) (см. табл. 4.1). Постоянная т3 — это и инерционность усилителя, и эффективное время наблюдения, и эффективное время накопления. В § 3.5 было также показано,

Что относительная частотная характеристика усилителя является спектром его относительной импульсной характеристи­ки Я (ДО - Поэтому к характеристикам Н{&), к([) применимы те же закономерности, что и для сигнального импульса Єе(£) и его спектра <?с(/)> которые были получены в § 2.1.

1. Площадь под кривыми /іа(Д£) равна максималь­

Ному значению частотной характеристики (значению на нуле-

Вой частоте)

Со

А (М) ^ А, (ДО еіАІ=А (ДО х,=к (0) = 1. (4.35)

Из (4.35) следует, что тэ можно определить не только как длительность /1Э(Д0, но и непосредственно по максимальному значению /^(Д^м):

Тэ= 1/Л (Д^м) •

Раньше (4.36) было получено для частного случая одно­звенного /^С-фильтра (4.13), теперь же оно получено для про­извольного фильтра. Рассчитанные по (4.36) значения тэ при­ведены в табл. 4.1.

2. Закономерность, обратная первой: площадь под кривой к(1) равна максимальному значению импульсной характери­стики

(4.37)

Отсюда по аналогии с формулой для сигнала (2.15) получаем определение эффективной полосы фильтра-усилителя:

/у=1/2та.

Из (4.37) следует, что полоса /у есть площадь под кривой к (0, или окно пропускания, характеризующее способность фильтра передать спектр сигнала соответствующей ширины. Напомним, что такое наглядное определение справедливо при симметричной характеристике Н(Д/), т. е. для фильтров І, II (см. § 2.1). При несимметричной импульсной характеристике (в нашем случае это ЯС-фильтры) (4.37) надо уточнить, учесть в ней по аналогии с (2.18) фазочастотную характеристику, однако (4.38), определяющее эффективную полосу /у, останется справедливым и в этом случае.

Шумовая полоса белого шума. Вклад в выходной шум бе­лой составляющей определяется первым членом подкоренного выражения (4.34):

Йг

= (4.39)

О

Из (4.39) видно, что шумовая полоса для белого шума [ш-б, т. е. такая эффективная полоса, в которой проходит на выход этот шум, определяется площадью под кривой к2Ц), а не под кривой к([), как было в случае сигнала. Полоса [ш-б ши­роко используется в радиотехнике (см. § 3.1 и 3.2). Рассчитаем ее значение для четырех рассматриваемых нами фильтров: фильтр с прямоугольной частотной характеристикой

ОС ^ у

. $***/-$.................................................................... . (4.40)

Оо ' ;

Фильтр-нак-опитель с временем накопления Та

О

__ П___ 1_.

~^лТн 2 ~~2ТН; однозвенный 7?С-фильтр

О

* : (4.41)

>к"а/

О о ф о :

= 2лтф~ агс1ь * |0 = , ^4‘42^

Двухзвенный ^С-фильтр

ОО оо оо

С = С _ 1 С Ах _ * Л _ * (А 43

И Л (1+шг1^,)г 2ятФ 3 (1+^)а 2дтф 4 8тф‘

Полученные значения /ш-б также сведены в табл. 4.1, Как видно из табл. 4.1, шумовая полоса /щ. б меньше или равна эф­фективной полосе усилителя для сигнала

А = /ш. б//у, -^1^1. |4.44)

Полученную закономерность легко объяснить для фильтров, У которых к (/)^0, ^у(/)=0. Для таких фильтров эффективная полоса сигнала определяется площадью под кривой &(/), а эта

240

Площадь не может быть меньше площади под кривой ’(т. е. шумовой полосы), так как &(/)^1. Чем круче спад ча­стотной характеристики такого фильтра, тем меньше отли­чается шумовая полоса от эффективной. Для рассмотренных фильтров отношение этих полос Г і лежит в пределах 0,5... 1.

Шумовая полоса для высокочастотного шума. Второй член подкоренного выражения (4.34) определяет высокочастотную компоненту шума

(4.45)

Ситуация здесь несколько сложнее, чем при белом шуме, когда спектральная плотность была постоянной, выносилась за знак

Оо

Интеграла и все сводилось к интегралу /окЩ, имеющему размерность частоты, — он и определял шумовую полосу /щ. б (4.39). При ВЧ-шуме его спектральная плотность растет с ча­стотой пропорционально /2, поэтому получаем интеграл размер­ности [Р] (4.45). По этой причине его нельзя непосредственно взять в качестве определения шумовой полосы.

Поэтому выберем значение спектральной плотности ВЧ-шу - ма на некоторой фиксированной частоте. Пусть это будет частота /у, и условно считаем входной спектр однородным, рав­ным фиксированному значению /2= (2лСвхеш/у)2. Такая спек­тральная плотность Я в некоторой полосе /ш-в должна дать ре­альную дисперсию выходного шума (4.45)

Из (4.46) следует определение шумовой полосы для ВЧ-шума

(4.47)

Как видим, теперь с размерностью все в порядке. Рассчитаем значения ^.в для тех же четырех фильтров:

Фильтр с прямоугольной частотной характеристикой

Фильтр-накопитель с временем накопления Гн

00 со

/ш. а~и РКЧ/^ р Л/ =

О о

^ $п2хйх^ 00; (4.49)

Однозвенный ДС-фильтр

TOC o "1-5" h z оо оо 00

Л..~5ЯМ/= ] 5«: (4.50)

О о

Двухзвенный /?С-фильтр

ЭС с®

X 1 С /2дГ/ 1 С

/:г"3' 7?.) (1+со24)2 _/уа(2ятф)> ^(1+^)*

1 11 _ 1 1 . МСП

/у2 (2яТф)3 4 {2л/уТф)г 8хф ’

По аналогии с (4.44) можно ввести коэффициент Г2 — отно­шение двух характеристических частот:

Оо

Гг=/ш,//у^Я*Ч/) <*////• (4-52)

О

Значения /ш'В (4.48) — (4.51) и Г2 (4.52) также сведены в табл. 4.1.

Частота |ш. в является специфичным параметром ФПУ. Что­бы мощность шума на выходе ФПУ была конечна, частотная характеристика должна спадать достаточно резко (/с~1/^):

Оо оо со

5 *»/«*/ = 5 ^ PйfЛ (4.53)

'у >у Гу

Из (4,53) видно, что интеграл сходится при 2(п—1)>1,

Т. е. при показателе л. >1,5. Фильтры 2, 3 не удовлетворяют этому условию и непригодны для использования в ФПУ с ВЧ-шумом. В фильтрах 1, 4 частотная характеристика спадает резко (п>1,5), поэтому шумовая частота /ш. в имеет конечное значение. Значения коэффициента Гг для фильтров /, 4 доста­точно близкие 0,33 ... 0,51.

Рассмотренные интегралы аналогичны интегралам, введен­ным Персоником при анализе шумов ФПУ для волоконно-опти­ческих линий передачи [85].

Граничная частота широко используется в радиотехнике. Усиление на этой частоте спадает до некоторого заданного уровня (например, до 0,7 от максимального значения). Значе­ния граничной частоты /07 приведены в табл. 4.1.

Общее выражение расчета для отношения сигнал-шум в квазиоптимальном фильтре. Вернемся к (4.34) для дисперсии шума и заменим в ней интегралы на введенные шумовые по­лосы:

£/ш = ~Ь(2яС0х£ш/у)2 /щ. в —-

= -(- (2яСвх£ш)2 /• (4.54)

Получили рабочее выражение, позволяющее по известной эффективной полосе усилителя /у (или постоянной времени тэ=1/2/у) рассчитать дисперсию шума на его выходе. Соб­ственно форма частотной характеристики фильтра (при их оди­наковой полосе /у) достаточно слабо влияет на шум. В приве­денных примерах коэффициенты Л, Г2 меняются в ограничен­ных пределах: 0,5 .,. 1 и 0,33 .. . 0,51 соответственно, так что относительные изменения шума составляют Um~V Г — = 0,7 ... 1; иш~ 1/^2 = 0,58 ... 0,71 (с учетом сделанной ого­ворки о выборе необходимой крутизны спада частотной харак­теристики) .

Выражения для расчета амплитуды сигнала как функции эффективной постоянной времени для фильтров с ^С-звень­ями— это формулы (4.19) и (4.29). Так что теперь можно со­ставить и искомое выражение для отношения сигнал-шум

^с/ш «^^сА^са/^ш

~SEcaUca/Уfу---{2лСвхе^х/у)'2Г2/уг /*у=1/2тэ. (4.55)

При очень узкой полосе /у отношение Nc/ш мало из-за ма­лого числителя (сигнала иса), а при очень широкой полосе оно падает из-за большого значения знаменателя (большого шума). Поэтому должно существовать некоторое оптимальное значение полосы /У) при которой это отношение достигает своего макси­мума. Из качественного анализа (начало § 4.1, рис. 4.4) оче­виден принцип выбора такой оптимальной полосы: она должна равняться эффективной полосе оптимального фильтра /yopt. При белом шуме последняя совпадает с полосой сигнала /с» так что

/у=/с> Ту—Гс, ’(4.56)

А при преобладании ВЧ-шума

■

{ Г 00 00 5,°°

=/BarctgЈj; = ^-/B; (4*57)

243

Теперь остается лишь подтвердить расчетом выбор уЖе достаточно очевидных значений (или несколько уточнить эти значения), а также найти достижимые в квазиоптимальных фильтрах с такой полосой значения Л^/ш.

Белый шум. Рассмотрим однозвенный ЯС-фильтр. Восполь­зуемся сначала аппроксимацией (4.19) для амплитуды выход­ного сигнала исл- Подставляя ее в (4.55) для отношения сиг­нал-шум и удерживая составляющую только белого шума, по­лучаем

Дт 5 № ^ т, ^ЕсАТс

Мс(ш—'

У 2*иг1/чтс + 4 у2я, я^{Тс + ч)

: (4.58)

УЩш (тс1УЧ) + Ухф

Здесь учтено, что для однозвенного фильтра Г 1 = 1/2; /у = == 1 /2тэ = 1/2тф. Двучлен в круглых скобках подробно рассмот­рен в § 2.5, его экстремум достигается при равенстве слага­емых:

* = ту = тф = Гс. (4.59)

V Т'ф

Для фильтра с такой оптимальной постоянной времени из (4.58) получаем следующее отношение сигнал-шум:

Та^ с)ш--=5Ясл1/Гс/1'а29/ш. (4.60)

А поделив формулу (4.58) на (4.60), получим кривую на­стройки однозвенного фильтра:

Л'с/ш/тах JV с/ш — 2/(У Т с/тф уУ т^/Т с). (4.61)

Так заготовленная аппроксимация для амплитуды выход­ного сигнала позволила упростить все расчеты, выполнить их в аналитическом виде. Но надо помнить, что при Тф — Тс эта аппроксимация на 9% (точнее, на 8,7%, рис. 4.8) занижает амплитуду сигнала. Поэтому (4.60) следует несколько уточ­нить:

Шах ЛГС/Ш= 1,09 SEcA УТс/У2дГш. (4.62)

Строго говоря, несколько уточняется и настройка фильтра. Численный расчет с использованием точного значения ампли­туды выходного сигнала (4.15) дает оптимальное значение по­стоянной фильтра Тф = 0,84Гс. Впрочем, этот факт имеет лишь теоретический интерес: кривая настройки столь пологая, что При изменении ПОСТОЯННОЙ Тф от Тс до 0,84ГС отношение Агс/ш

Растет лишь на 0,45% (более точное значение коэффициента в (4.62) 1,092).

Аналогичен расчет и для двухзвенного фильтра. И опять понадобится аппроксимация для амплитуды выходного сигна­ла— на этот раз это (4.29). Подставляя ее в (4.55), получаем при преобладании белого шума:

5£СА_____ Гс____________ ^СА^С________

У'2^/ш//у Угс’+V у

Т/Т 5£сд-КГс т/ 2 ’ ,ле^

= У е ущй У Гс/Тз + Тэ/Гс • ( '63)

И вновь расчет оптимальной постоянной времени фильтра

Связан с поиском экстремума выражения в круглых скобках ви-^ да (х~у/х). Минимум этого двучлена достигается при равен­стве его слагаемых (см. § 2.5):

Гс/тэ = тэ/Тс; тэ = етф = Тс. (4.64)

Таким образом, максимальное значение отношения сигнал - шум достигается при выборе постоянной времени каждого зве­на Тф=Тс/е и по (4.63) равно

= (4.65)

У е У 2д! т V 2д1ш

Б соответствии с (4.63), (4.65) кривая настройки двухзвен­ного фильтра

Л^ш/тахЛ^/ш = у'2/(Гс/тэ + тэ/Гс). (4,66)

Использованная аппроксимация для амплитуды выходного сигнала двухзвенного фильтра еще точнее, чем для однозвенно­го: при тэ —Тс она завышает сигнал лишь на 2,7% (рис. 4.10). Строгий читатель может соответственно уменьшить коэффи­циент в (4.65):

Шах^с/ш=1Л85ЯсА’К7’с/1/2^/Ц1, (4.67)

Причем это значение достигается при несколько большей эф­фективной постоянной времени, чем было рассчитано с по­мощью аппроксимации, — при Тэ = 1.057*0

Каков комментарий к выполненным расчетам? Конечно, не терпится провести сравнение с оптимальным фильтром. Вспом­ним: выражение для отношения сигнал-шум оптимального фильтра ЛГс/ш (3.72) отличается от полученных выраже­
ний (4.62), (4.67) только коэффициентом. Он равен V3/2 = = 1,22. И коэффициент потерь составляет: для однозвенного ^С-фильтра

/7=тах А^с/ш/7Ус? щ= 1,09/1,22 =0,89; (4.68)

Для двухзвенного /?С-фильтра

Л= 1,18/1,22 = 0,965. (4.69)

Конечно, после проведенного качественного анализа нас не удивишь малыми значениями коэффициента потерь. И все же полученный результат превзошел все ожидания: двухзвенный

#С-фильтр проигрывает оптимальному в отношении А/с/ш всего 3,5%! Так что такой фильтр даже неудобно называть «квази».

Как и предполагалось, максимум отношения сигнал-шум достигается, когда эффективная постоянная времени фильтра равна (почти равна) длительности сигнала (4.59), (4.64) или, что то же самое, эффективная полоса фильтра равна полосе сигнала. Однако кривые настройки /?С-фильтров очень поло­гие, (рис. 4.11 и (4.61), (4.66)). Это дает возможность раз-

Высокочастотный шум. Однозвенный НС-фильтр в этом слу­чае непригоден, так как он не обладает нужной крутизной спада частотной характеристики. Поэтому в качестве квази- юптимального рассмотрим только двухзвенный ^С-фильтр. Для определения отношения сигнал-шум такого фильтра позаим - ствуем из предыдущего раздела формулу (4.63), восстановив в ‘ ней составляющую высокочастотного шума: лг 5£сД Гс

А' с/ш

V*шР 1/у + (2лСвхеш)‘ ^""г/у* 5£сАГс

(4.70)

(‘2лСвхешу Г

+

2. <%1 ш Г

Заменяя по (2.138) и табл. 4.1 2д! ш1 (2пСвхеш2)-^}в2, /УЛ"* -*е2/я2, учитывая, что /у=1/2т3, т9^>ТС> преобразуем выраже­ние в фигурных скобках к виду

- [ 2 (*Фе + (2Я/.)» е «ф )} {2.1/, [ 2 (V". + чйа )]]• (4-71)

Опять получили знакомый двучлен вида *+1/*, экстремум ко­торого достигается при равенстве его слагаемых, т. е. при ра­венстве белой и высокочастотной составляющих шума. Поэтому постоянная времени каждого звена и эффективная постоянная времени фильтра в целом должны удовлетворять условиям

Тф(оа= 1/тф0в; Тф=1/шв; тэ — етф = е/(2л;/в). (4-72)

Отклонение от предсказанного значения эффективной посто­янной времени квазиоптимального фильтра (4.57) всего в е}2~ 1,36 раз.

Подставляя в (4,70) преобразованное выражение в фигур« ных скобках (4.71), а также значение Л = е/4, получаем для от­ношения Л^с/ш

ЗЕ'.ьТс

О^.д/ £ Г О

ЛГс, ш=-т=!к^=-1/_

12^7ш Т 2л/7 Т|,,Ш" + Тфш1

? /2я—‘----------------------------------- Ц—. (4.73)

У^Ш V ТфО>,+ —

При настройке фильтра тф©в=1 значение последнего под­коренного выражения равно единице, и, следовательно, макси­мальное отношение сигнал-шум достигает значения

ТахЛ'с, ш=-2-у'2й-^==- У~/,, (4.74)

А кривая настройки совпадает по форме с кривой настройки при белом шуме и двухзвенном фильтре:

NC|m/max NCjЩ^V2/(тфо)в4- 1/тфсов). (4.75)

В (4.74) появился коэффициент 2/е = 0,735 (сравните с соот­ветствующей формулой (3.77) для оптимального фильтра). Как видим, двухзвенному ^С-фильтру труднее справиться с ВЧ-шумом, чем с белым, но и в этом случае потери в отноше­нии сигнал-шум около 26,5% можно считать вполне приемле­мыми. Кривая настройки представлена на рис. 4.13.

Несколько слов о форме выходного сигнала. Поскольку полоса квазиоптимального фильтра значительно уже полосы сигнала, то последний можно считать дельта-импульсом и вы­ходной сигнал повторяет по форме импульсную характеристику ;(та же ситуация, что и при оптимальной фильтрации, § 3.6). Импульсная характеристика двухзвенного йС-фильтра была представлена на рис. 4.6,6. Ее форма заметно отличается от колоколообразной — затянут срез, а длительность по уровню 0,5 значительно превышает длительность входного сигнала и рас­считывается по (4.28), (4.72):

Гс/в<С1; 705/7лс = 2,45тф/Тс = 2,45/7с (2л/в) =

=0,39/ГС/В, / (4.76>

Двухзвенный ^С-фильтр можно использовать в качестве квазиоптимального и в общем случае, когда белая и высоко­частотная составляющие шума сопоставимы. Выражение (4.70), в котором учтены обе шумовые составляющие, дает возмож-

НОСТЬ найти н условие настройки, и коэффициент потерь в от­ношении сигнал-шум. Приближенные выражения получим из предельных формул для преобладающего белого (4.64), (4.67). либо высокочастотного шума (4.72), (4.74), используя ту же методику, что и при конструировании (3.98) для оптимальной фильтрации:

Х, = Тс+е/2я/е; (4.77)

ЛГС,«.=0,835ЯЯсд VI?/У 2?/ш (1 +0,82//в2Гс). (4.78)

Погрешность полученных формул составляет 30%. По­скольку использована одинаковая методика «конструирова­ния» приближенных формул для отношения Л^с/ш как в случае оптимальной (3.98), так и квазиоптимальной (4-78) фильтра­ции, то неудивительно, что они совпадают по своей структуре, лишь численные коэффициенты 0,865 и 0,48 заменены в случае квазиоптимального фильтра на 0,835 и 0,82.

Низкочастотный шум. Способ фильтрации в этом случае стоит особняком от только что рассмотренных, поскольку надо формировать не только высокочастотный, но и низкочастотный спад частотной характеристики. Так появилась схема, содержа­щая и интегрирующее, и дифференцирующее ^С-звенья '[(рис. 4.5,в). Частотная характеристика фильтра составляется из частотных характеристик этих ЯС-звеньев

* Н=1+уДф‘1 + уШТф. (4.79)

Для удобства анализа постоянные звеньев Тф выбраны оди­наковыми. Простейшим преобразованием

^ (гЛ______ /й>Тф + 1 — 1 1 1 /л от

К 01 (1 +/оЛГф) (1 +уо>Тф) ~1~У10Тф (1+УЮТф)11 ( 4 '

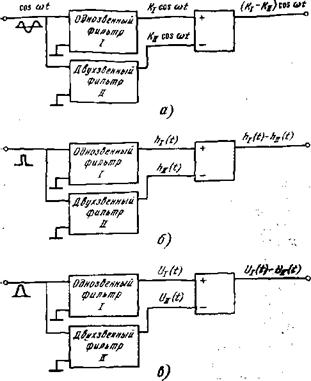
Приходим к очень любопытному результату. Фильтр синтези­руется из двух, только что рассмотренных однозвенного и двух­звенного, их входы включаются параллельно, а выходные сиг­налы вычитаются (рис. 4.14). Если на вход такой составной схемы подать гармонический тест-сигнал (рис. 4.14,а), то вид­но, что частотная характеристика соответствует (4.80). На рис. 4.14,6 на вход подан дельта-сигнал, и импульсная харак­теристика тоже является разностью импульсных характери­стик тех же фильтров (4.11), (4.23):

Й(Д^) = -^-ехр ( — Д^/Тф)---------- ~ехр(—Д*/тф) =

Тф

—(1 — Дг/тф)ехр ( — Д*/тф). .(4.81)

Тф

Наконец, на рис. 4.14,6 на вход подан косинусквадратный сигнал. Естественно, что выходной сигнал оказывается раз - ( ностью найденных для этого случая выходных сигналов одно - и двухзвенных фильтров. На рис. 4.15 прилежно выполнено ука-

• занное вычитание (построена разность кривых на рис. 4.7 и

* 4.9) и получен выходной сигнал квазиоптимального фильтра

■ при НЧ-шуме. На рис. 4.16 представлена амплитуда этого сиг­нала в зависимости от постоянной времени Тф. И оптимальный, и квазиоптимальный фильтры при таком шуме являются дифференцирующими, соответственно в их выходных сиг­налах есть общее — отрицательный выброс. При очень малых значениях постоянной времени фильтра сигнал «зАрезается» дифференцирующим звеном

(штф/|/ 1 4'с°2тф')> а при очень большой постоянной —интегри­рующим (1/]/7 Поэтому должно существовать опти­

Мальное значение постоянной времени, при которой сигнал мак­симален. Из рисунков видно, что максимум сигнала дости-

_

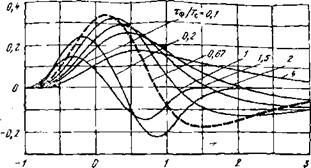
Рис. 4.15. Форма сигнала на выходе квазиоптимального фильтра с дифференцирующим и интегрирующим звеньями в зависимости от Тф (входной сигнал коло- колообразный)

Гается при Тф = 0,67Тс, а его относительное значение равно 0,34, поэтому.

^са(^)=0,34 5£са. (4-82)

Здесь была нарушена наша традиция получать все основ­ные результаты аналитически. Однако нетрудно получить каче-

Ственную оценку значения максимального сигнала, не прибе­гая к численным методам расчета. Для такой оценки понадо­бится всего пять шагов и рис. 4.17, где последовательно пред­ставлены сигналы на входе (рис. 4.17,a), a также на выходе одно - и двухзвенного фильтров (рис. 4.17,6,в).

1. Выбираем постоянную времени. Для этого можно и не обращаться к рассчитанным кривым uc(t, Тф). Общее прави­ло — необходимость согласования полосы квазиоптимального фильтра с полосой сигнала — диктует условие Тф=7с-

2. Согласно аппроксимации (4.19) сигнал на выходе одно­звенного фильтра при тф=Гс равен

ЫсА1 = Тс/ (Тф+Тс) = Те1(Тс+Тс) = 1/2. (4.83)

3. Максимальное значение достигается в момент (4.21)

/ = /м = Гтф/(7’с-ЬтФ)]Гс = [7'с/(7,с+Гс)]Гс = 0,5Гс. (4.84)

4. Казалось бы, самое сложное — это определить отклик двухзвенного фильтра в этот же момент времени t = Q,6Tc, Но если привлечь методику § 3.6 и использовать импульсную ха­рактеристику, точнее, ее прямоугольную аппроксимацию (рис. 4.17,г), то такая оценка окажется несложной. Ведь в первом приближении фильтр можно рассматривать как интег­ратор на интервале тэ. Конкретно для момента ^ = 0,5ГС выход­ной сигнал есть интеграл от входного на интервале [t, t2] (рис. 4.17,г), т. е. искомая амплитуда пропорциональна за­штрихованной площади сигнала на рис. 4.17, а. А она составля­ет примерно 60% площади всего входного импульса еСкТ<:^ТСг следовательно,

Вс 11 (<») « h (<„) 0,6 Тс = 4- 0.6 Гс=0.6 Тс/ехф = 0.22. (4.85)

ТЭ

5. Максимум относительного выходного сигнала примерно равен

^са ^ ИсАх—Исц (^м) »0,5—0,22 = 0,28. (4.86)

Традиция восстановлена — удалось аналитически оценить порядок значения амплитуды выходного сигнала (ср., (4.82), (4.86)).

Теперь необходимо рассчитать шум на выходе рассматрива­емого фильтра

______ °° 00

I (грп-)’ "-ъ'-f-т S TTW -

О©

— З^Ulfn ^

. При избыточном входном шуме вида 1// шум на выходе во­обще не зависит от полосы фильтра — его постоянной Тф (см.

, 3 3)

И, наконец, итоговая формула отношение сигнала (4.82) к шуму (4.87) принимает вид

Л^/ш = ^са/^ш = 0>345£‘са/У? Лп/и =

= 0,485£'са/1^2*7/ш/*к • , (4.88)

Из (4.80), (4.88) следует, что потери квазиоптймального филь­тра при НЧ-шуме

Я-^»/^с°?ш = 0,48/0,6=0.8 (4.89)

Оказываются меньше, чем при ВЧ-шуме.

Кривая настройки ЛГс/ш(тф) на рис. 4.16 повторяет кривую настройки сигнала, поскольку шум не зависит от постоянной Тф. Исключения нет — кривая Лгс/Ш(тф) при избыточном шуме тоже пологая, как и все остальные кривые настройки.

Весь анализ проведен для одинаковых постоянных времени дифференцирующего Тф. д И интегрирующего Тф звеньев. Ко­нечно, можно выполнить громоздкие расчеты, выбрав эти по­стоянные независимыми и с помощью раздельной оптимизации попытаться снизить коэффициент потерь. Но, во-первых, мак­симально возможный приз — выигрыш в отношении Лгс/Ш не более 20%. А во-вторых..., а во-вторых, такой расчет по­казывает, что выбор одинаковых ^С-постоянных звеньев опти­мален и дальнейшее снижение коэффициента потерь в подоб­ной схеме невозможно. Конечно, сказанное относится к рассмотренному случаю «чистого» избыточного шума, пре­обладающего во всем спектре сигнала (/н> 1/2Гс). Если же избыточный шум заметен лишь на относительно низких часто­тах /н<С1/2Тс, то дифференцирующее звено должно отсекать только эти частоты (тф. д«1/2я/н). Поскольку вырезаемая по­лоса (в окрестности нулевой частоты) узкая по сравнению с полосой сигнала, то такая фильтрация слабо влияет на вы­ходной сигнал и долю белого шума — они практически сохра­няются такими же, как при белом шуме и однозвенном интег­рирующем фильтре.

Сколько звеньев должен содержать квазиоптимальный фильтр? Нами были предложены квазиоптимальные фильтры Для всех спектров шума, которые вероятны в ФПУ, определе­ны коэффициенты потерь предложенных фильтров. И на во - прос: сколько надо выбирать звеньев? ответили: один-два зве - На> причем указали, какие именно звенья. Что же заставляет вновь задавать вопрос о числе звеньев? Это частота ложных тРевог, оценка которой еще не проводилась. Вспомним опре­деление этой частоты (3.22). Учитывая, что при произвольном ®ходном спектре 0 спектр на выходе ФПУ равен ввых = ^2@>
получаем для характеристической частоты, определяющей ин­тенсивность ложных тревог:

ркща///ш - /ш - V Кща/. (4.эо>

О о

При преобладании белого шума частота /ш» стоящая в знаменателе, есть шумовая полоса /ш-ь, а при преобладании ВЧ-шума она пропорциональна полосе /ш-в - Эти шумовые по­лосы уже рассчитаны (4.42), (4.43), (4.51). Найдем теперь интеграл в числителе (4.90):

Белый шум (однозвенный фильтр)

]pKmfJ^p_lLAdf^x, (4.91)

О а ф о

Белый шум (двухзвенный фильтр)

00 оо со

Pdf _ I jj хЧх. '

(4.92)

ВЧ-шум (двухзвенный фильтр)

00 оо оо * ■

Ркщй/=^ Р ‘ т-8 °° • <4-9з>

$ % (*+®Ч) /в I

Стоило ли тратить усилия на вычисление трех интегралов,, чтобы получить столь неутешительные результаты: два интег­рала расходятся, и лишь при белом шуме и двухзвенном филь­тре частота ложных тревог оказывается конечной. К расхо­димости приводит подынтегральный член р@, поэтому фильтр» а он представлен в подынтегральной функции множителем /с2, и должен компенсировать сильное возрастание указанного чле­на. Сходимость интеграла будет обеспечена при 12Э2к2<С (В//). При белом шуме этому условию удовлетворяет фильтр, содер­жащий как минимум два звена:

/-►ОО. /202/^2 __ /2. 1------------- (4.94)

(1+®=4) /

А при ВЧ-шуме — фильтр с тремя и более звеньями:

/->О0, ^202^2^/2/1------------------ 1--------- ОО (4.95)

' 7 } /в* (1+<0Ч2ф)* /-

Значит ли это, что прежние предложения несостоятельны: при белом шуме нельзя использовать однозвенный, а при ВЧ-шуме — двухзвенный фильтры? Что все приведенные для
этих фильтров расчеты напрасны? Положение облегчается тем, что дополнительное звено, обеспечивающее более крутой

Высокочастотный спад коэффициента передачи фильтра, может иметь малую постоянную времени Тф1 по сравнению с постоян­ной времени основных ЯС-звеньев Тф. Расчет по (4.80) показы­вает, что при таком малоинерционном звене характеристиче­ская частота /хар возрастает всего в (0,4 . .. 0,7) Утф/тф, раз (относительно своего значения при симметричных звеньях Тф — тф]). Так что если даже тф/тф! = 10 ... 100, то частота лож­ных тревог увеличивается лишь в 4... 7 раз. В § 3.1 было по­казано, что такое возрастание частоты ложных тревог некри­тично — указанное увеличение компенсируется повышением порога срабатывания всего на 4... 20%. А само значение ха­рактеристической частоты ложных тревог двух-, трехзвен­ного симметричного фильтра (4.89) с точностью до 30% совпа­дает как с частотой /у, так и с /ш.

Из сказанного следует, что постоянная времени дополни­тельного звена может быть выбрана весьма произвольно и быть значительно меньше постоянной времени основного звена. Разработчику труднее обеспечить широкополосность системы, а падение коэффициента передачи на высоких частотах (/» да1/2з1тф]) может происходить из-за ограниченности инерцион­ных свойств микросхем, наличия паразитных емкостей. По­этому при разработке ФПУ обычно нет необходимости специ­ально создавать дополнительное ^С-звено. Этот вопрос, как правило, решается одновременно с устранением самовозбужде­ния схемы. Поскольку постоянная времени основных звеньев значительно больше, чем дополнительного, то характеристиче­ские частоты /у, /ш-б, /ш-в формируются основными звеньями и все приведенные расчеты сигнала, шума и их отношения оста­ются справедливыми.

Подведем итог. Оптимальный фильтр не только трудно синтезировать, зачастую он просто физически нереализуем. К счастью, нет необходимости в точном воспроизведении частотной характеристики оптимального фильтра, так как отношение сигнал-шум достаточно слабо зависит от формы частот­ной характеристики фильтра. Достаточно синтезировать фильтр, согласован­ный по полосе с оптимальным и имеющий необходимую крутизну спада частотной характеристики. Такой фильтр называют квазиоптимальным. В ФПУ он составляется с помощью самых простых ^С-звеньев, причем до­статочно одного либо двух таких звеньев: интегрирующих при белом и ВЧ - Шуме, интегрирующего и дифференцирующего при НЧ-шуме. Лучше всего «справляется» такой фильтр с белым шумом. Он уступает оптимальному в отношении сигнал-шум МС/ш всего 3,5... 11%, так что этот фильтр даже неудобно называть «квази», он практически является оптимальным. Не­сколько выше потери в отношении Л'с/ш при избыточном и высокочастотном Шуме — 20 и 26,5% соответственно.

4.2. ШИРОКОПОЛОСНОЕ УСИЛЕНИЕ И ЛАВИННОЕ УМНОЖЕНИЕ

При оптимальной и квазиоптимальной фильтрации необхо­димо ограничивать полосу частот: при белом шуме она долж­на соответствовать полосе спектра сигнала, а при БЧ-шуме по­лоса выбирается значительно уже — не пропускаются частоты с большим ВЧ-шумом. Сигнал на выходе фильтров с ограни­ченной полосой всегда затягивается по сравнению с входным. Однако в ряде оптико-электронных систем возникают ограниче­ния на допустимые искажения формы выходного сигнала. Прежде всего это системы с последовательностью импульсов. Первый пример — обнаружение нескольких близко расположен­ных точечных целей. В длйнновременной релаксации сигнала от первой цели может «потонуть» сигнал от близко располо­женной второй цели (особенно если первая цель яркая, а яр­кость второй цели мала). Другой пример — волоконно-оптиче­ские системы передачи; заданное быстродействие заставляет ограничивать время релаксации каждого информационного им­пульса так, чтобы он не накладывался на последующий. Тре­тий пример — выходное устройство ПЗС, которое должно ус­петь зарегистрировать за заданное время опроса каждый от­дельный импульс от последовательности зарядовых пакетов (см. § 4.6).

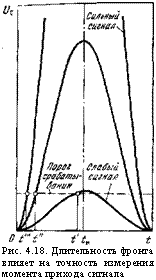
Ограничения на затягивание выходного сигнала могут воз­никать даже при обнаружении одиночного оптического импуль­са, если требуется не только обнаружить, но и измерить поло­жение этого импульса во времени [88]. ФПУ для таких систем обычно строятся по схеме обнаружителя, а временное положе­ние импульса определяют по моменту срабатывания порогового устройства (рис. 4.18). Фронт и, следовательно, длительность выходного сигнала здесь приходится ограничивать из-за того, что от них зависит точность измерения: при слабом сигнале наиболее вероятно срабатывание порогового устройства в мак­симуме сигнала а при сильном — в момент прихода это­

Го сигнала

Так возникает необходимость использовать в ФПУ для ука­занных систем, как правило, широкополосный усилитель с бо­лее широкой эффективной полосой пропускания, чем у опти­мального (квазиоптимального) фильтра. Появляется тема на­стоящего параграфа: по допустимому искажению выходного

Сигнала, например допустимой длительности Т05, найти требу­емую постоянную времени /?С-звена Тф (полосу широкополос­ного усилителя, как и квазиоптимального, формируем /^С-звень­ями). Необходимо рассчитать и коэффициент потерь в отноше­нии Л’с/Ш такого широкополосного усилителя по сравнению с оптимальным. Все это позволяют сделать формулы и графики § 4.1. В широкополосных системах на авансцену выходят ЛФД»

И вновь встает вопрос об оптимизации их режима работы, преимуществах по сравнению с обычными ФД. Такой анализ уже проводился в § 2.5 для единичной полосы. Теперь его надо повторить при широкой полосе усилителя.

Белый шум. Эффективная постоянная времени при белом шуме не слишком большая — равна (или несколько меньше) длительности входного сигнала, поэтому расширение выходного сигнала должно быть умеренным. С помощью аппроксимаций

(4.20) , (4.30) можно получить аналитическую оценку длитель­ности выходного сигнала по уровню 0,5: однозвенный ^С-фильтр

Тф = 0,84ТС; То,5 = Тс+тф 1п2 = ГС+0,84ГС 1п2= 1,58ГС; (4.96)

Двухзвенный ДС-фильтр

Ч=тс/е. г 05 =. у 7У+6т|= у ГС2+67'СУ<?2= 1,34ГС.

К сожалению, аппроксимация для однозвенного фильтра в ок­рестности значений Тф = Гс имеет заметную погрешность (рис. 4.8,6). Впрочем, нетрудно определить и точное значение длительности 705, ведь на рис. 4.8,6, 4.10,6 приведены также зависимости 70б(тф), полученные численным расчетом. С по­мощью этих зависимостей при оптимальной настройке фильтра - усилителя по максимуму отношения сигнала к шуму получаем: однозвенный ^С-фильтр

Тф = 0,84Гс; 705=1,427с; двухзвенный 7?С-фильтр тф = 0,3857с; 705=1,357с

Такое умеренное затягивание длительности сигнала на

30.. . 40% для ряда систем может быть приемлемым. А если все-таки потребуется воспроизводить форму входного сигнала с еще большей точностью, то, естественно, придется расширить полосу усилителя, снизив постоянную времени ^С-звеньев (рис. 4.8,6, 4.10,6). Задавшись допустимым расширением сиг­нала Т’об/Гс, найдем значение тф, а по нему можно с помощью рис. 4.8 и 4.10 определить и отношение сигнал-шум, и амплиту­ду выходного сигнала. По данной методике на рис. 4.19 по­строены ВСе Необходимые ЗаВИСИМОСТИ Тф(Г05), Л^/шС^сз), Ыса(То5)> которые характеризуют прохождение сигнала через широкополосный усилитель. В § 4.1 отмечено, что пологая кри­вая настройки фильтра Лгс/ш(тф) предоставляет разработчику достаточную степень свободы в выборе Тф. Воспользуемся этой свободой. Выбирая, например, тф—(0,35 ... 0.48) Гс всего на 10% увеличиваем длительность выходного сигнала (по сравне­нию с входным). И цена за такое расширение полосы фильтра не слишком высока: потери в отношении Л^/ш вырастут только на 14 ... 10% (рис. 4.19).

Аналогично можно рассчитать зависимости от постоянной тф и других временных параметров сигнала, например длительно­сти фронтов, положения максимума, и при необходимости на­страивать фильтр по этим параметрам. Обычно здесь тоже можно обойтись без заметного снижения коэффициента потерь.

К сожалению, при регистрации коротких — прежде всего лазерных — импульсов преобладают ВЧ-шумы (см. § 2.3), и ситуация становится далеко не такой благополучной.

Высокочастотный шум. Рассмотрим случай, когда в спектре сигнала 0.../с преобладает высокочастотная составляющая шума — она превышает белую составляющую, начиная с низ - ких частот /в- Сразу же введем отношение /с/7в — оно войдет во все основные формулы. Для наглядности анализа будем про­водить численные оценки на примере типичной задачи — обна -

Сужения короткого лазерного импульса с длительностью Тс = = 10-8... Ю'7 с. В соответствии с табл. 2.2 принимаем Ря = = 2- Ю2... 4- Ю4 Гц и

/с-1/2Гс = 1/2(10-8... 10-7)=5(106... ю?) Гц,

/с//в= 120 ... 2,5* 105. (4.99)

ВЧ-шум доминирует во всей полосе сигнала, оставляя менее сотой части этой полосы для белого шума!

Необходимую частотную характеристику усилителя будем формировать с помощью двухзвенного ^С-фильтра (одно ДС-звено не обеспечивает фильтрацию сигнала из смеси с ВЧ-шумом, § 4.1). При квазиоптимальной фильтрации полосу такого фильтра приходилось ограничивать низкими частотами

0. .. /в, где преобладал белый шум, что приводило к сильному затягиванию выходного сигнала (4.76). Согласно этой формуле

Г05/Тс = 0,39/Гс/в - 0,78/ (2ГС)/В = 0,78/с//в=

= 0,78(120 ... 2,5-105) ^ 100 ... 2 -105. (4.100)

Уже в (4.100) мы сталкиваемся с отношением /с//в, которое в этом случае показывает, что выходной сигнал затягивается практически в /с/7в раз. Так что речь идет о затягивании не на

30.. . 40%, как при выделении сигнала из смеси с белым шу-. мом, а на два порядка и более! Поэтому в быстродействую­щих ФПУ приходится отказываться от настройки фильтра по частоте /Б и настраивать его на полосу сигнала [с. Выбираем постоянную фильтра Тф = ^7"с так, чтобы обеспечить допусти­мое затягивание сигнала [Тоб/Тс]. Поэтому значение у не зави­сит от характера шума и находится с помощью рис. 4.19, а, как и при белом шуме. А можно воспользоваться достаточно точной аппроксимацией (4.30), согласно которой

тк/тд -1/ Т сЧТ1+б1/Т,? = УТ+6^;

’Г = Тф/Гс = >/{[7'03/7’ср- 1>/6 =

= У{(1Л... 1,4)2- 1}/б «0,2 ... 0,4. (4.101)

Здесь численная оценка ^ приведена для систем, в которых допускается затягивание сигнала на 10... 40%. Эффективная полоса усилителя при такой постоянной фильтра будет равна

/у= 1/2тэ—1/2етф= 1/2еуТс={с/еу & (0,9 ... 1,8) ?с. (4.102)

Благодаря такой широкой полосе относительная амплитуда выходного сигнала исл достаточно большая. Ее значение также, можно найти с помощью рис. 4.19 либо аппроксимации (4.29):

^сА== ^-^сА^сА»

Ис^Тс/УТ'*+(еч)2 = 1 /V1 +И)2=

= 1/У 1 + [е (0,2 ... 0,4)]2 »0,68 ... 0,9. . (4.103)

Специфика шумового спектра при настройке широкополос­ного фильтра-усилителя по сигналу сказывается только в рас­чете среднеквадратичного значения шума. Увеличение полосы приводит к резкому возрастанию этого шума (по сравнению с квазиоптимальной фильтрацией). Из (4.54) и (4.102) получаем

Ит - у (ГОуж = Ущ

; = У 2дІщ/{4г[ УЩ) уІ2л/в7І/2. (4.104)

Здесь использовалось определение характеристической частоты ВЧ-шума (2я/вСвхеш)г = 2<7/ш, а значение Гг взято из табл. 4.1. Для отношения сигнала (4.103) к шуму (4.104) получаем

•^с/ш ~ ЗЕсИс/ит =

. = (4-( Уяч йса) 5£сА7'|/2/./1/2?/ш -

' ={4-(У^^У7/в}іУ&8Ее„ТсУГ,/УЩ^І (4.105)

Эта формула заслуживает самого подробного анализа. Отметим новую, уже четвертую степенную зависимость ЛГс/щ от дли­тельности входного сигнала. При оптимальной (квазиоптималь­ной) фильтрации и преобладании НЧ-шума отношение сигнал - шум вообще не зависело от длительности Е^Т^, при

Преобладании белого шума Лґс/Ш~ £са УТс высокочастотного Агс/Ш ~£’са7лс (см. § 3.4). Теперь, когда доминирует ВЧ-шум и приходится выбирать широкую полосу усилителя, отношение сигніл-шум еще сильнее зависит от длительности — получили закон «трех вторых» АгС|Ш~£,сЛГс/2. Столь сильная зависимость объясняется тем, что сама спектральная плотность мощности

Шума растет с ростом частоты пропорционально /у2, полная мощность во всей полосе усилителя £/ш~ДЛ так что средне­квадратичное значение шума ищ = V ~/у/2. Полоса широ­кополосного усилителя настроена на спектр сигнала (4.102), поэтому тот же показатель «трех вторых > сохраняется и по отношению к длительности Гс.

Характер зависимости Лгс/ш~£'са7’с'1 обусловливает выбор инварианта обнаружения ФПУ, вспомним § 3.4: для НЧ-шума МЫ вводили пороговую МОЩНОСТЬ [ЯсАІпор» для белого —порог (£саУГс Іпор и для высокочастотного — пороговую энергию [ЯсдГ^пор (§ 3.4). Теперь также можно ввести инвариант обнаружения И, т. е. такую интенсивность оптического импуль­са, при которой отношение сигнал-шум равно единице. Из (4.105) следует, что пороговая интенсивность является специ­фической величиной [£’са7'с/2]поР’ КОТОрЭЯ связана С порогом в единичной полосе следующим образом:

И =EzTc ]лор = т/&S f s - Ф^/af (4.106)

Где

А = 4лт ]2f исА.

В § 3.4 отмечалось, что в лазерных системах обычно ограни­чена энергия накачки лазера — энергия сигнала ЕсАТс — const. Тогда, если исходить из классического случая белых шумов и оптимальной фильтрации, очень выгодно уменьшать длитель­ность сигнала с точки зрения обнаружительных характеристик (а не только с точки зрения временного разрешения), посколь­ку в этом случае

ЛГ,„~Ес* VTt =£саГс/УТ7=,const/vr; . . (4.107)

При преобладании ВЧ-шума и постоянной энергии сигнала его длительность переставала влиять на отношение ДОс/ш~£са7с = = const. Закон «трех вторых» вовсе испортил ситуацию. Теперь при ВЧ-шуме и широкополосном усилителе укорачивание им­пульса (при постоянной энергии) не только не облегчает, а, наоборот, затрудняет обнаружение:

Мс<а,~£сг!,2 = £сГсУГс = const J/TT. (4.108)

Если разработчики оптико-электронных систем продолжают мыслить классически и рассчитывают на уменьшение порого - вой энергии коротких оптических импульсов, то их придется разочаровать: за быстродействие системы надо расплачиваться повышением пороговой энергии импульса. Неумолимый закон «трех вторых» подводит и разработчиков многоэлементных си­стем. Ожидая улучшения обнаружения с ростом числа элемен­тов ФПУ, можно столкнуться с совершенно обратным эффек­том — при очень большом числе элементов приходится уменьшать время опроса Тс, и, когда шумы выходного широ­кополосного усилителя становятся доминирующими, начинает расти пороговая энергия (пороговый заряд). С этим эффектом еще встретимся в § 4.6.

Теперь пришло время расплачиваться за быстродействие нашего усилителя. Одна из форм выражения для отношения Nc/m (4.105) специально представлена как произведение двух сомножителей. Сомножитель в квадратных скобках — это отно­шение сигнал-шум оптимального фильтра N c/L (см. (3.77)). Поэтому другой сомножитель в фигурных скобках непосред­ственно называет цену расплаты — он является коэффициентом потерь широкополосного фильтра-усилителя в отношении NCfla по сравнению с оптимальным:

Я = Л'с/Ш/=21УЩ,1ИсА V «

«(0,4... 1,2)У7771~ 10-3 ... 10->. ' (4.109)

Вряд ли можно мириться с таким ухудшением, если важны обнаружительные характеристики системы. Поэтому одной из основных задач разработчиков широкополосных ФПУ является борьба с ВЧ-шумом (повышение /в). Приемы этой борьбы об­суждались в § 2.5, но основной способ подавления ВЧ-шума усилителя заключается в использовании лавинного умножения.

Лавинное умножение при широкополосном усилении. Преж­де всего оценим предельные возможности ЛФД: во сколько раз можно улучшить отношение Л'с/Ш в широкополосном ФПУ, ес­ли заменить в нем обычный ФД на лавинный? Для наглядно- сти вернемся к «прямоугольному мышлению»: считаем полосы сигнала и широкополосного усилителя прямоугольными и по­лагаем /у=/с= 1 /27'с (§ 3.3). В таком случае цса=1» и на вы­ходе ФПУ с обычным ФД без умножения имеем для сигнала и шума

С/с=5ЯсА, о/у +

6 /в

(4.110)

Их отношение

Л'фпу ФД = 5£-сА/1/2?/0/сз/з/в2. (4.111)

Теперь рассчитаем отношение для ФПУ на основе ЛФД. Идеализируем модель: пусть лавина не шумит (х = 0, § 2.3) и ее усиление не ограничено; удалось устранить тепловой шум и все утечки, так что белая компонента определяется только умножаемым током ФП. В таком идеализированном ФПУ с идеализированным ЛФД в М раз усиливается и сигнал, и шум ФП и при достаточно большом значении коэффициента умно­жения шум ФП окажется больше шумов усилителя:

С/ М5Е с А> ит = У 2д{ $М2/с + 2#/о/ с/3/в2 ~

ЖМУЯдТо. (4.112)

Тогда отношение сигнал-шум на выходе ФПУ станет равным

Агфпу лфд = М5£’сА / М 1/2<7/0/с = ЗЕсА/ У2д10/С. (4.113)

Собственно говоря, формулы (4.111) и (4.113) представляют собой отношение сигнал-шум для ФПУ на основе обычного ФД, только в первой из этих формул расчет проведен с уче­том ВЧ-шума усилителя, а во второй учитывается только собственный шум ФД. Так наглядно показано, в чем преимуще­ства лавины: в результате умножения и сигнал, и собственный шум фотоприемника удалось «вытащить» над шумом усилите­ля (о чем уже говорилось в § 1*2 и 2.5).

ФПУ не справился со своей задачей —не смог реализовать собственное отношение сигнал-шум в фотоприемнике, испор­тил его шумами своего усилителя. ЛФД пришел ему на по­мощь— идеальная лавина полностью подавляет шумы усили­теля. Благодаря этому получается большой выигрыш в отноше­нии сигнал-шум:

А^фпу лфд/А^фпу фд — ^- = / с/КЗ/з^

У 2д10/с

= 0,58/с//в. (4.114)

И вновь в (4.114) вошло отношение /с//в- Идеальное умно­жение позволяет повысить отношение Мс/Ш во столько раз, во сколько полоса сигнала /с больше частоты /в (с точностью до коэффициента). Нет необходимости пояснять, почему возникла именно такая зависимость — это объясняют (4.111) и (4.113). На коэффициент в (4.114) влияет форма частотной характери­стики усилителя. Для интерсующего нас двухзвенного /?С-фильтра из (4.114) и табл. 4.1 получаем

Агфпу Лфд/Агфпу фд = У 2ql0Г2/yV/e2/У^2#/оГf у —

= (VTVA) (/у//в) = (VeVrt2) (/сМ/в) = /с/ЯТ/б =

= /с/л (0,2 ... 0,4) /в — (0,8 ... 1,6) /с//.»

«100 ... 4* Ю6. (4.115)

Лавинный фотодиод настолько превосходит ФД, что выбора уже не остается: в пороговых широкополосных системах надо применять только ЛФД.

К сожалению, в реальных ЛФД шум при умножении ра­стет быстрее сигнала, поэтому, как только этот шум заметно превосходит шумы усилителя, дальнейшее повышение умно­жения становится невыгодным — оно уже ухудшает отношение Л^с/ш. Эта особенность ЛФД учитывается при выборе оптималь­ного режима его работы — выборе коэффициента М (см. § 2.5). От перестройки полосы ФПУ с узкой на широкую ме­тодика выбора режима не меняется: смещением рабочей точки ЛФД повышают его умножение до тех пор, пока мощность шу­мов ЛФД не превзойдет начальную мощность шума — шума усилителя — в некоторое заданное число раз п, причем 8=51 ... 3. Из этого условия рассчитывается коэффициент умно­жения в таком режиме. Сначала перепишем выражение для шумов (4Л12) с учетом расшумливания ЛФД — введем коэф» фициент шума к (§ 1.2), а также ради общности учтем тепло - вую и дробовую составляющие шума усилителя:

~ f у[ j ~j~ и^.у, 6гщ. у = 2^Гу/уГ1 -{-

+4-^лг1+^-/уза. Aus»

Откуда

2q/0Mti’,fyrl=,aUry. (4-117)

Индекс при коэффициенте умножения напоминает о том, что при указанной методике режим работы ЛФД является квази - оптимальным; методика установки оптимального режима суще­ственно сложнее, а выигрыш в отношении Nс/ш незначителен (см. § 2.5).

С учетом (4.116) и (4.117) выражение для отношения сиг­нал-шум примет вид

Агф пу лфд — MmSEckack/V2?/0AfSVy^i (1 + l/n)—- =SEcaU-ca/^2ql0Af Ј, fyrt (1 + 1/«). (4.118)

Реальность всегда уступает идеалу, сравните формулы (4,113) и (4.Ц8): избыточное «расшумливание» ЛФД привело к появле - НИЮ ДОПОЛНИТёльног0 множителя /Икв и, как следствие, к не­полному подавлению шумов усилителя (множитель Мкв2)- Соот­ветственно и выигрыш в Отношении ТУс/щ из-за замены ФД на

ЛФД будет меньше в ~f М*в{ -И/я) Раз* чем Для идеализи­рованного ЛФД (4.115). Чтобы провести здесь численную оценку, надо сначала оценить коэффициент уИкв. Из (4.116), (4.117), табл. 4.1 при х = 0,2; п = 2; /у-^0; #н->-оо следует, что этот коэффициент теоретически должен быть равен

_1_ _2_______

= (rc'VA)2+* (/у//в)2+’' ~80 ... 1,5-103. (4.119)

И здесь приходится назвать еще одно отступление реаль­ных ЛФД от своего идеала: их коэффициент умножения огра­ничен (в кремниевых ЛФД, как правило, значениями Afmax^ « 100 ... 200, § 1.2), что является самым неприятным недо­стАтком. Для указанных значений Л/шах, п множитель

У ЛГтах (I + 1/я)»2, так что пока нужны ограниченные умно жения (Мкв^200), реальные кремниевые ЛФД уступают иде­альному бесшумному ЛФД по отношению сигнал-шум в эти

2 раза. Но если ВЧ-шумы очень велики, то реальный ЛФД не может развить нужного умножения для подавления этого щу, ида -—не может обеспечить Мкв>200. в этом случае замена ФД на ЛФД приводит просто к увеличению сигнала в Мтах раз на фоне постоянного шума усилителя.

Лавинное умножение при оптимальной (квазиоптимальной) фильтрации. Если при широкополосном усилении полоса фильтра строго фиксировала и выбирается в зависимости от допустимого искажения формы сигнала, то при оптимальной и квазиоптимальной фильтрации эта полоса отслеживает измене- ние частоты /в. С ростом коэффициента умножения эта частота возрастает, поскольку умноженный дробовой шум фотоприем­ника «забивает» ВЧ-шум до больших частот:

/, = /„Л12+х; /,==/2д1<,М2+х/«>С„еш = /воЛ-11+'"'2;

/й='/2?/0>о)С„еш. (4.120)

Указанное отличие в выборе полосы фильтра обусловливает и различную роль лавины в этих двух режимах. Только что было показано, что лавина при широкой полосе усилителя спо­собна на один-два порядка улучшить отношение сигнал-шум, поскольку изначально (без лавины)очень сильно ухудшается это отношение из-за большого вклада мощности ВЧ-шумов. В этом смысле возможности лавины при оптимальной фильтрации значительно скромнее. Сам фильтр частично справ­ляется с ВЧ-шумом, отсекая высокие частоты, где этот шум преобладает, и не допускает столь сильного изначального па­дения отношения ЛГс/ш. как эт0 было при фиксированной широ­кой полосе.

Еще раз повторим сказанное, но уже на языке формул. Ме­тодика выбора квазиоптимальных значений М1ГВ сохраняется прежней. До тех пор пока коэффициент умножения меньше квазиоптимального и ВЧ-шум остается доминирующим, спра­ведливы формулы для отношения сигнал-шум (3.77) и (4.74), поэтому после ряда преобразований

ЛГс/ц,=<Ш5£сАГс У7./У^1=

= (аЛ«ЯсдГс/1/2^7;) ]/75?77/<аС„вш= ч>Свкеш у 2?/,=

=аЦ15ЕсьГс/УтСпеш V2дIВ/И2+“ =

=а5£'с47'сЛ10’5-“/4/)/ ЮСшешУ2чГ0, (4.121)

Где а—У2л —для оптимальной фильтрации; а = 2у2я/е —для квазиоптимальной. Если при широкой полосе фильтра-усилителя отношение сигнал-шум возрастает пропорционально коэффи­
циенту Л4, то при оптимальной полосе возрастает значительно слабее-пропорционально /'Л1.. .У М. Как только достигнуты квазиоптимальные значения умножения, шум «выбеливается», и для отношения Ыс/Ш получаем те же (почти те же) предель­ные значения, что и при широкой полосе (4.113) и (4.118). Ка­кой же максимальный выигрыш в отношении МС|ДД дает лави­на? Как и прежде, оценим этот выигрыш, используя прямо­угольные аппроксимации для спектров сигнала и шума. Если в широкополосном и оптимальном фильтрах максимальные зна­чения А! с/т при идеальной лавине оказались почти одинаковы­ми, то начальные значения №С/ш (без умножения) существенно различаются. Вспомним § 3.3: спектральная плотность сигна­ла в оптимальной полосе частот 0.. ./в равна 2Еса. Тс, а мощно­сти шума — 2 ^/0> так что сигнал, шум во всей полосе и их от­ношение равны

^с-25£сАГс/в> } агфпуфд^-2—с—

Ит = У2ц/0и } У 2#/о/в

25£сАГсУ7в У2д10

Это начальное значение А/фпу фд намного лучше, чем при ши­рокой полосе усилителя (4,111). Поэтому замена ФД на ЛФД приводит не к столь разительному выигрышу: поделив (4.113) на (4.122), заменив 1/2 Тс=/:с» получим

Л^фпу лфдЛУфгту фд — 5ЕС д/с У 2^/0/]/ 2?/0/с ЗЕсА у/, = =У77Г.- (4.123)

Опять выигрыш зависит все от того же отношения частот

И/и, но теперь он пропорционален не первой степени, как при широкой полосе (4.123), а только корню из этого отношения,

Перестройка фильтра (расширение его полосы 0.../в с ро­стом умножения) приводит также к уменьшению длительности выходного сигнала. При умножениях, меньших квазиоптималь - ных, пока преобладает ВЧ-шум, длительность сигнала по (4.100), (4.120) падает обратно пропорционально умножению или даже несколько сильнее:

^=0,78/с//в = 0,78/с//воЛ11+*'г. (4.124)

Когда шум выбеливается, длительность выходного сигнала всего на 28% превышает длительность входного (§ 3.6 и 4.1)» Так что лавина исправляет те недостатки, которыми страдает ФПУ на основе ФД. При широкой полосе это особенно плохое отношение N с/ш, а при оптимальной полосе — инерционность и весьма посредственное отношение А^/щ.

Подведем итог. При оптимальной (квазиоптимальной) фильтрации поло­са пропускания всегда ограничена, что приводит к затягиванию выходного сигнала. В ряде оптико-электронных систем такое затягивание недопустимо и приходится выбирать полосу фильтра шире, чем в оптимальном. Правда, при белом шуме и оптимальной (квазиоптималыгай) фильтрации расшире­ние сигнала умеренно — около 30... 40%, так что увеличение полосы в 2... 4 раза обеспечивает, как правило, нужную инерционность при незначи­тельном снижении отношения сигнал-шум (10... 15%). Однако при больших ВЧ-шгмах усилителя (превышающих белый шум с частот /Е) полоса опти­мального (квазиоптимального) фильтра 0...[в значительно уже полосы сиг­нала 0 ... /с Это приводит к затягиванию сигнала в /с//в раз, что обычно составляет несколько порядков. Расширение полосы усилителя до полосы сигнала обеспечивает быстродействие, но резкое возрастание доли ВЧ - шумов ухудшает отношение сигнал-шум примерно в /У/в раз.

Идеальное лавинное умножение полностью подавляет ВЧ-шум, тем са­мым исправляет недостатки ФПУ на основе ФД и позволяет реализовать собственное отношение сигнал-шум ФП. При широкой полосе ФПУ устра­няются указанные потери в отношении сигнал-шум — оно улучшается в те же Раз- При оптимальной фильтрации устраняется затягивание сигналов в /сЯв раз и также улучшается отношение сигнал-шум примерно в У /с/Тв раз (здесь выигрыш меньше, чем при широкой полосе, когда из-за ВЧ-шума отношение особенно сильно падало в отсутствие умножения).

В реальном ЛФД сказываются шумы лавины, коэффициент умножения ограничен и не удается полностью подавить ВЧ-шумы усилителя. И все же замена ФД па ЛФД способна улучшить отношение сигнал-шум на один-два порядка