Методы расчета валовых ресурсов в точке А (ф°,у°) и для заданной территории £ (км ) для горизонтальной приемной площадки при ограниченном составе исходной информации для среднесуточных или месячных расчетных интервалов
Как было сказано выше в гл.2, солнечные энергетические установки могут эффективно использоваться сегодня в системах энергоснабжения по трем основным сценариям: работа в большой энергосистеме, работа в локальной энергосистеме и работа на локального или автономного потребителя. В зависимости от принятого сценария использования СЭ возникают дополнительные сложности в расчетах, включая и необходимость наличия разного рода исходной информации о приходе СР так и необходимость решения проблемы получения достаточно достоверной информации в расчетных точках, в которых полностью
Отсутствуют любые данные фактических наблюдений о приходе СР. Последний случай весьма характерен для условий современной России, для которой более 2/3 ее территории с населением 8-10 млн человек не подключены к системе централизованного энергоснабжения при наличии в этих регионах достаточно значительных ресурсов СЭ, которые успешно можно использовать для энергоснабжения автономных потребителей.
У7
В этом случае для всей территории бывшего СССР для расчета Эвал и Эвал (5) можно воспользоваться известной формулой Ангстрема, которая предполагает наличие некоторых среднесуточных или среднемесячных данных по СР как в точке А (ф°,у°), так и для территории
5 (км2):
Тфакт
ЭГакт (D) = ЭГ (At) • (а + b - р-), (3.10)
Сс
Г 2 2
Где Эфакт (АҐ) - (кВт*ч/м ) или (кВт*ч) для территории £ (км ), соответствует среднемноголетнему значению прихода СР на
Горизонтальную площадку за Аґ равный 1 суткам или 1 месяцу; Эя (АҐ) -
22 (кВт*ч/м ) или (кВт*ч) для территории £ (км ) - приход СР за Аґ, равный 1
Суткам или 1 месяцу на горизонтальную площадку на поверхности
TOC o "1-5" h z Г Г
Земли при абсолютно прозрачном и ясном небе, когда Эх (АҐ)= Эпр (АҐ) и рассчитывается по формуле:
— Г —Г
Эя (At) = Rпр(At)• cos#(At)-At, (3.11)
Г 2
где Rnp (At) (Вт/м ) - среднеинтервальная мощность прямого СИ на нормально ориентированную к СИ приемную площадку, которая может быть определена по формуле:
SHAPE \* MERGEFORMAT ![]()
— Г —г
R пр (At) = R пр (AM 1)'
/_ а (AMm-1)
R пр (AM 1)
Ro
(AMm-1)
= 1000 •( — I, (3.12)
Г 2
Где Rnp (АМ1) (Вт/м ) - стандартная среднеинтервальная мощность СИ в южных широтах Земли на уровне моря при абсолютно прозрачной
Атмосфере для горизонтальной ПП на поверхности Земли (равно 1000
2 2 2 Вт/м ); R0 (Вт/м ) = 1360 Вт/м - солнечная постоянная или приход СИ на
Нормальную к СИ ПП площадью 1 м в космосе на границе атмосферы
Земли; АМт (о. е.) - атмосферная масса т или оптическая масса
Атмосферы, рассчитываемая по формуле:
M(At) = , 2_ --------- @ , , 2------------ , (3.13)
2
|
Cos 6 (At) +----- + cos 6 (At) |
![]() • La + cos6 (At) Vcos2 6 (Dt) + 0,06 + cos0 (At)
• La + cos6 (At) Vcos2 6 (Dt) + 0,06 + cos0 (At)
Где т(А?) - среднеинтервальная атмосферная масса атмосферы за интервал А? (о. е.); 0(А£) (град.) - среднеинтервальный угол падения Солнца за интервал А?; Ьа (км) - тоЛщиНа, слоя атмосферы в рассматриваемой точке А (р°, у°); гз (км) - расчетный радиус Земли в точке А (р°, у°).
При этом значение cos в (А?) в (3.11) рассчитывается следующим образом:
Соб0°(Л?) = э1п8°(Л?)• э1пр° + соэ8°(Л?)• соэр°• ^ад, (3.14)
Где cosв (А?) (град.) - среднеинтервальный угол падения Солнца за интервал А?; 8° = 8° (А?) - склонение Солнца за интервал А?, которое обычно определяется по формуле Купера:
8°(Д?) = 8, ■ э1п(^ ■ (284 + п) (3.15)
V365 0
Где 8о = 23°27' = 23,45°; п (о. е.) - порядковый номер дня года,
Отсчитываемый с 1 января. Тем самым принимается, что значение 8° (А?) =
8° (п), т. е. склонение Солнца считается постоянным для каждого п-го дня года, а 284 - константа, равная числу дней года, начиная с 21.03 и до 31.12;
А3(град) - часовой угол захода Солнца на горизонтальной площадке, определяемый из соотношения:
Г р ■ / л
Ооб а 3 (А/) = ооб ° ■ tgS °(А/), (3.16)
V 12 0
Где /3(час) - моменты восхода-захода Солнца, определяемые условием:
О = ±90° и, следовательно,
А д = агс^(^ф ° ■ tg8 °(А/)), (3.17)
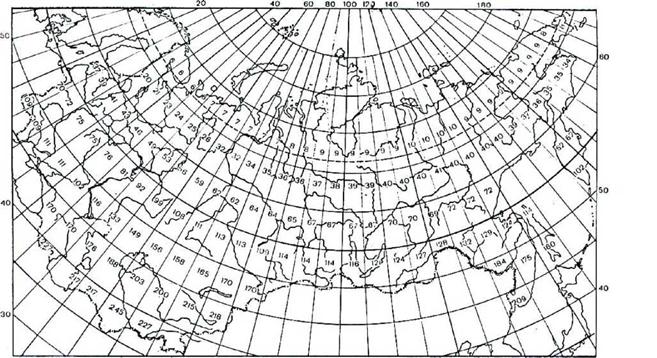
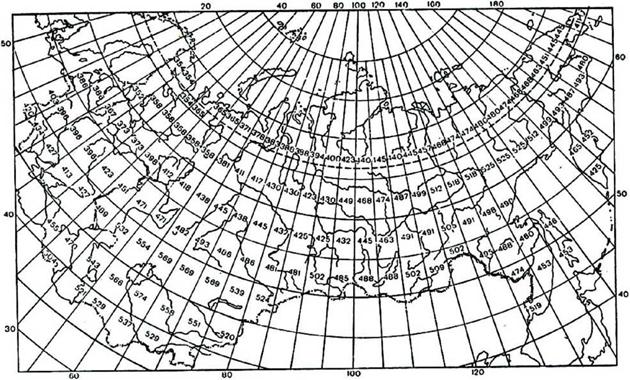
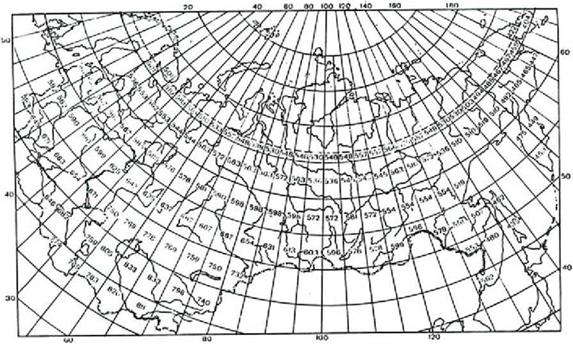
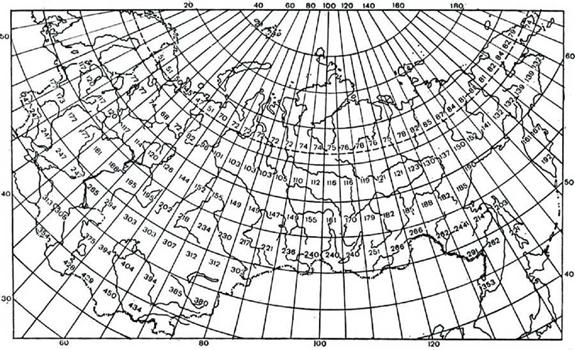
Эмпирические константы "а" и "Ь" в (3.10) рассчитаны для 144 трапеций всей территории бывшего СССР размером, как правило, (5° х 5°) и принимаются постоянными внутри каждой трапеции, т. е. а = а (ф°,у°) и Ь = Ь(ф°,у°) при условии что а + Ь = 1. При этом "а" характеризует собой пропущенную облаками долю СР на Земле, а "Ь" - задержанную облаками долю солнечной радиации на Земле на горизонтальной площадке. В отличие от США, где константы "а" и "Ь" - постоянны в течение всего года, для огромной территории бывшего СССР с резко изменяющимися географическими и климатическими условиями константы "а" и "Ь" задаются для четырех характерных для каждого сезона года месяцев (1, 4, 7, 10) при линейной интерполяции их значений между характерными месяцами. Рассчитанные эмпирические константы по территории бывшего СССР представлены в виде карт, опубликованы в Метеорологическом ежемесячнике и представлены на рис. 3.1-3.4.
Указанные в нем трапеции (5° по широте) расположены южнее 70° северной ШиРоты. В качестве примера в таблице 3.1 приведены предельные значения "а" для бывшего СССР и значения "а" для г. Москвы.
В метеорологическом ежемесячнике приводятся также данные по фактической продолжительности солнечного сияния в заданные характерные сутки каждого расчетного месяца - Тссфакт(час). При этом
Ошибка экстраполирования данных по Тссфакт(час) по указанным выше трапециям (характерное расстояние - 200 км) составляет до 5% в летний период и до 10% в зимний период.
|
Би НО 100 120 Рисунок 3.1 Средняя многолетняя месячная сумма суммарной солнечной радиации по площади 5-градусных трапеций (МДж/м ). Январь |
|
Рисунок 3.2 Средняя многолетняя месячная сумма суммарной 2 Солнечной радиации по площади 5-градусных трапеций (МДж/м ). Апрель |
|
Рисунок 3.3 Средняя многолетняя месячная сумма суммарной 2 Солнечной радиации по площади 5-градусных трапеций (МДж/м ). Июль |
|
Рисунок 3.4 Средняя многолетняя месячная сумма суммарной 2 Солнечной радиации по площади 5-градусных трапеций (МДж/м ). Октябрь |
|
Таблица 3.1 Предельные значения а(о. е.) для бывшего СССР и г. Москвы
|
Наконец, приведенные в (3.10) значения Тссо(час) соответствует теоретической продолжительности солнечного сияния или нахождения середины солнечного диска над горизонтом при абсолютно прозрачном небе, определяемого по формуле (1.16).
К недостаткам формулы Ангстрема следует отнести следующие:
1. Неопределенность расчета Эя (А?), из-за сложности учета изменений атмосферы в понятии «ясного дня».
2. Неопределенность расчета Тссфакт (час) для рассматриваемой трапеции, поскольку здесь многое зависит от способов измерения фактической продолжительности солнечного сияния (визуально или по приборам), характеристики местности и других условий.
В связи со сказанным выше одновременно с формулой Ангстрема в мировой практике принято использовать и ее модернизированный вариант
- формулу Пейджа:
|
( —факт 9 19 Т С А + Ь - — |
|
— Г —Г Э факт (М) = Э0 (М) |
|
- о V Тсс 0 |
 |
|
|
|
В (3.18) в отличие от формулы Ангстрема должны быть введены "новые" (модернизированные) значения констант а' и Ь' для каждой расчетной по территории региона трапеции. Кроме того вместо Эя (А?)
Здесь используется значение прихода СР на горизонтальную ПП в космосе
Г2
На границе атмосферы Земли - Эо (п) (кВт-ч/м - сутки), которое может быть найдено по формуле (1.21).
С учетом всего сказанного выше можно определить валовые ресурсы СИ как в заданной точке А(ф°,цг°), так и для территории площадью £ (км ) следующим образом.
Если точка А(ф°,цг°) находится внутри какой-то из 144 трапеций на территории бывшего СССР, то для нее определяется по формуле
Ангстрема значения Э факт ( 2—д—■—) для характерных суток
Г - подёе
Четырех месяцев года, а также для всех остальных месяцев года с использованием линейной интерполяции между смежными во времени
Года значениями констант "а". Полученные значения Э факт (—2——-—) для
Г - подёё
Каждого месяца года умножаются на число суток в каждом месяце и суммируются между собой, определяя валовые ресурсы СИ в точке
А(р°, у°).
Если точка А(р°,у°) находится вне территории бывшего СССР, то аналогичный расчет может быть проведен с помощью международной базы данных КАБА по прилагающимся к ней инструкциям.
Если рассматриваемая территория площадью £ (км ) располагается внутри одной из 144 расчетных трапеций на территории бывшего СССР, то для нее находится значение валовых ресурсов СИ по алгоритму, изложенному выше для точки А(р°,у°) и полученное значение умножается на площадь £ в м2.
Если же указанная территория площадью £ (км ) находится в двух или более расчетных трапециях на территории бывшего СССР, то выделяются частные площади указанной территории, приходящиеся на каждую расчетную трапецию и для них производятся расчеты аналогичные представленным выше. Далее, полученные результаты по каждой расчетной трапеции суммируются между собой, определяя искомое значение валовых ресурсов СИ для территории £ (км ).
При использовании международной базы данных КАБА расчет валовых ресурсов для территории £ (км ) несколько усложняется не меняя своих принципиальных положений, изложенных выше в данном параграфе, а также п. 3.1.