ПЕРВЫЙ В МИРЕ ВЫЧИСЛИТЕЛЬНЫЙ АВТОМАТ
Во Франции в Парижском «Музее искусств и ремёсел» с конца прошлого века хранится интереснейшая счётная машина. Это — первый в мире автомат для вычислений, изобре* тённый в 1881 году знаменитым русским математиком и механиком академиком П. Л. Чебышевым.
Изобретение академика Чебышева намного опередило все существовавшие тогда счётные машины и оказало большое влияние на весь ход дальнейшего совершенствования «машинной математики». Созданию этого замечательного автомата предшествовало изобретение Чебышевым в 1878 г. оригинальной суммирующей машины. Оригинальность её заключалась главным образом в способе передачи десятков. Никакого специального механизма для выполнения этой операции она
вообще не имела, хотя передача десятков, конечно, осуществлялась. В машине Чебышева, как и во всех счётных машинах, при полном обороте цифрового колеса единиц цифровое колесо десятков поворачивалось на ]/10 оборота.
|
Окошко Счетчика |
![]()
|
Установочные Колёса |
![]()
|
Шкала на кожухе |
![]()
|
Цифровое колесо счетчика |
![]()
|
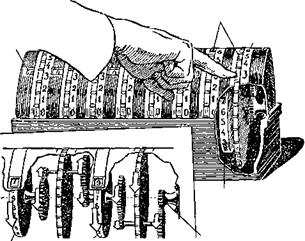
Рис. 22. Суммирующая машина академика П. Л. Чебышева с бесступенчатой передачей десятков. |
![]()
|
Неподвижной ль 'шестерня Цифровое Цифровое Колесо Установоч - колесо Установоч - десятков ное колесо единиц мое колесо десятков единии |

|
Полного оборота цифрового колеса, а постепенно — по мере накопления единиц, причём она сразу же распространялась и на последующие разряды. Стоило цифровому колесу единиц повернуться на 1/хо оборота, чтобы колесо десятков повернулось на 1/т оборота, колесо сотен на ]/100о и т. д. Оригинальность механизма передачи десятков, предложенного академиком Чебышевым, заключалась в том, что цифровые колёса счётчика соединялись друг с другом шестернями, имеющими различное число зубцов. Известно, что если в паре шестерён одна имеет в два раза ббльшее количество зубцов, чем другая, то при вращении второй она совершит в два раза меньшее количество |
![ПЕРВЫЙ В МИРЕ ВЫЧИСЛИТЕЛЬНЫЙ АВТОМАТ подпись: полного оборота цифрового колеса, а постепенно — по мере накопления единиц, причём она сразу же распространялась и на последующие разряды. стоило цифровому колесу единиц повернуться на 1/хо оборота, чтобы колесо десятков повернулось на 1/т оборота, колесо сотен на ]/100о и т. д.
оригинальность механизма передачи десятков, предложенного академиком чебышевым, заключалась в том, что цифровые колёса счётчика соединялись друг с другом шестернями, имеющими различное число зубцов.
известно, что если в паре шестерён одна имеет в два раза ббльшее количество зубцов, чем другая, то при вращении второй она совершит в два раза меньшее количество](/img/563/image235.gif) В отличие от всех остальных конструкций передача десятков в машине Чебышева происходила не сразу, в момент
В отличие от всех остальных конструкций передача десятков в машине Чебышева происходила не сразу, в момент
Оборотов. В таком случае говорят, что шестерёнки имеют передаточное отношение 2:1.
Нетрудно догадаться, что для передачи десятков потребуется соединить цифровые колёса шестерёнками с передаточным отношением 10:1. Но при этом цифровые колёса будут вращаться в разные стороны (см. стр. 10). Вращение в разные стороны легко устраняется введением в конструкцию промежуточной шестерёнки, этого же можно добиться заменой одной пары шестерёнок с передаточным отношением 10:1 двумя парами с передаточными отношениями 2:1 и 5:1. Такая замена целесообразна ещё и потому, что делает машину более компактной. Именно так и поступил Чебышев.
Благодаря найденному им решению передача десятков происходила плавно и была неотделима от самого суммирования. Это была машина непрерывного действия.
Машину Чебышева постигла судьба многих отечественных изобретений: она не была реализована в царской России. Единственный экземпляр её, сделанный самим Чебышевым, попал во Францию. Там им немедленно воспользовался немец Зеллинг. Он в точности скопировал основные механизмы машины Чебышева и выдал их за своё изобретение.
Лжеавторство Зеллинга ещё в 1894 году разоблачил известный в своё время русский авторитет в области счётных машин В. Г. Бооль.
Отмечая оригинальность устройства вычислительной машины Чебышева, он писал: «На арифмометре Чебышева совершается постепенное передвижение десяти единиц низшего разряда в виде одной единицы на колесе высшего разряда, без перескакивания, как это делается в арифмометрах других систем. Такое же устройство имеет арифмометр Зеллинга... Изобретение Чебышевым своего арифмометра произошло почти за десять лет до изобретения Зеллинга. Конструкция машины представляет замечательное механическое устройство, при котором остроумно применяются одни и те же приёмы для исполнения разнообразных действий. Часть машины, назначенная для сложения, будучи взята отдельно, представляет собой лучшую из всех машин по своей простоте, точности и скорости исполнения на ней действий сложения и вычитания».
Но это разоблачение не помогло; Зеллинга продолжали считать изобретателем машин нового типа. Через четыре года Бооль в книге «Приборы и машины для механического производства арифметических действий» опять отстаивал приоритет
Чебышева в создании машины непрерывного действия! «Зел - линг даже ни одним словом не упоминает о том, что он заимствовал эту часть машины от Чебышева, и говорит, что способ этот составляет оригинальную особенность его машины. Так как машина Чебышева (часть её для сложения) изобретена в 1878 году, а машина Зеллинга в 1886 году, то не может быть никакого спора о первенстве изобретения, тем более, что эти 8 лет машина Чебышева находилась на выставке в Париже, где находится и теперь».
Не только Зеллинг воспользовался трудами русского академика. Принцип автоматизации вычислительного процесса, впервые разработанный Чебышевым, применяется во всех современных автоматических машинах, а американская фирма «Мерченд», швейцарская «Директ» и другие используют в своих конструкциях принцип передачи десятков, предложенный академиком Чебышевым.
Интерес к машине Чебышева понятен. Системе плавной передачи десятков принадлежит будущее. Современную науку и технику перестают удовлетворять скорости порядка 500 вычислений в час. Существенным тормозом дальнейшего увеличения скорости счёта на машинах является ступенчатая пере - дача десятков. Механизмы передачи десятков не успевают срабатывать на более высоких скоростях, особенно, когда надо передать десятки последовательно в нескольких разрядах. С этой задачей может лишь справиться механизм, построенный Чебышевым.
Итак, мы уже познакомились с разными машинами. Среди них были суммирующие и вычислительные, ручные, полуавтоматы и автоматы. Одни могут только считать, другие считать и записывать. Но есть у всех них общее. Всё это машины, которым человек выдаёт задание.
Да, без помощи человеческих рук они работать не могут. Человек должен произвести установку, то-есть сообщить машине, какими числами она должна оперировать, и после
Этого нажатием специальной клавиши указать, что должна
Сделать машина с этими числами: складывать, вычитать, перемножать или делить.
— А как же иначе? — удивится читатель. — Ведь не может же машина сама прочесть числа и догадаться, чего хочет
От неё человек? Оказывается, может..,