СВОЙСТВА МЕТАЛЛОВ

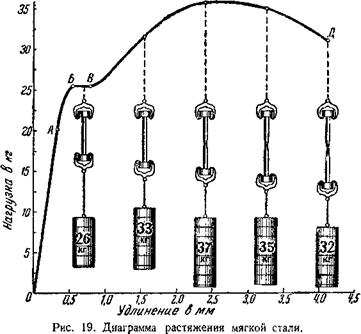
ПОКАЗАТЕЛИ ПРОЧНОСТИ И ПЛАСТИЧНОСТИ

Чтобы выяснить, как деформируется тот или другой металл при действии растягивающей силы, производят специальные испытания. Образец металла строго опреде­лённых размеров и формы укрепляют в захватах разрыв­ной машины. После этого образец подвергается растя­жению под действием плавно возрастающей нагрузки.

Посмотрим, как будет деформироваться проволока из - мягкой углеродистой стали (с содержанием углерода, до­пустим, 0,02%) сечением в один квадратный миллиметр и длиной 10 сантиметров (рис. 19).

Вначале удлинение строго пропорционально нагрузке: гиря в 10 кг вызывает удлинение в 2 раза большее, чем гиря в 5 кг гиря в 20 кг даёт удлинение в 4 раза боль* шее, чем гиря в 5 кг, и т. д. Короче говоря, какова сила, такова и деформация, — удлинение про­порционально величине растягивающей силы.

Если начать уменьшать величину растягивающей силы, проволока будет постепенно укорачиваться, и когда все гири будут сняты, она примет первоначальную длину. Так проявляются упругие свойства. При упругих деформа­циях безразлично, какие силы и в каком порядке действу­ют на тело. Можно сначала растянуть проволоку, затем закрутить её, а можно поступить наоборот — сначала за­крутить, потом растянуть. В обоих случаях поведение ме­талла будет одинаково: после прекращения действия рас­тягивающей и закручивающей сил проволока неизменно принимает первоначальную форму. Но так будет продол­жаться только до определённого предела — предела упругости. Для мягкой стали этот предел наступает при напряжении около 20 кг! мм2.

Пока напряжение не превышает предела упругости, отношение напряжения к вызываемой им деформации для каждого металла постоянно. Иначе говоря, частное, по­лученное от деления величины напряжения на относитель­ное удлинение (удлинение на каждый миллиметр длины проволоки), есть величина постоянная. Эту величину на­зывают модулем упругости (слово «модуль» по- латыни означает мера):

Напряжение

--------------- е--------------------- = модуль упругости.

Относительное удлинение

По модулю упругости можно судить о способности металла или сплава сопротивляться деформирующим си­

Лам. Чем больше модуль упругости, тем жёстче металл. Модуль упругости мягкой углеро­дистой стали равен 21 ООО кг/мм2, меди— 11 500 кг/мм2, алюминия 7000 кг/мм2. Таким образом, мягкая сталь почти вдвое жёстче меди и втрое жёстче алюминия. Де­рево — менее жёсткий материал, чем металлы: модуль упругости, например, сосны (вдоль волокон) равен всего 900 кг/мм2.

Продолжим опыт дальше и посмотрим, что произой­дёт, когда нагрузка будет превышать предел упругости.

В е с г и р ь, растягивающих проволоку, равен 21 кг, за­тем 22 кг, 23 кг. Проволока удлиняется уже больше, чем это было до предела упругости, и после снятия гирь уже не будет восстанавливать первоначальную длину: сталь начинает деформироваться пластически. Пластическая де­формация ещё не велика — остаточное удлинение соста­вляет всего-навсего тысячные доли процента.

Но вот нагрузка равна 26 кг. Проволока растягивается ещё больше. И что здесь интересно: несмотря на то, что напряжение не увеличивается, оно равно 26 кг, — удли­нение со временем растёт, сталь начинает «течь». Это — предел текучести.

При дальнейшем растяжении пластическая деформа­ция проявляется всё сильнее и сильнее. Внутренние силы упругости уже не могут противостоять внешней силе, растягивающей проволоку, и в кристаллах, повидимому, изменяется расположение атомов.

Наконец, наступает момент, когда в определённом ме­сте проволока начинает утончаться, образуется шейка. Для мягкой стали напряжение, при котором начинает по­являться шейка, равно примерно 37 кг! мм2. Это — пре­дел прочности мягкой стали, самое большое напря­жение, которое она способна выдержать. Чем выше это напряжение, тем прочнее металл.

Дальнейшая деформация происходит главным образом в шейке, уже без увеличения нагрузки. Для мягкой стали достаточно напряжения около 32 кг/мм2, чтобы шейка сузилась и произошел разрыв.

На рисунке 19 показано, как постепенно деформи­руется проволока, и дано графическое изображение всего нашего опыта по растяжению проволоки из мягкой стали — диаграмма растяжения. На вертикаль­ной оси отмечаются напряжения, а на горизонтальной оси откладываются соответствующие им удлинения прово­локи. Так как поперечное сечение нашей проволоки равно одному квадратному миллиметру, то напряжение, возни­кающее в ней, равно приложенной нагрузке. В местах пересечения горизонтальных линий, которые мы проводим от оси напряжений, с вертикальными (от оси, на которой отмечается удлинение) ставятся точки; затем они соеди­няются. Точка, обозначенная буквой Л, — предел упру­гости. Пропорциональность между нагрузкой и вызывае­мым ею удлинением, которую мы наблюдаем до предела упругости, выражается прямой линией ОА. Далее пропор­циональность нарушается — прямая линия переходит в кривую АБ. Горизонтальная площадка на кривой между точками Б и В соответствует пределу текучести: напря­жение одно и то же — 26 кг/мм2, а длина проволоки воз­растает. Точка Г — предел прочности, начало образова­ния шейки, точка Д — разрыв.

Нужно сказать, что площадка текучести БВ обнару­живается не у всех металлов. В таких случаях пределом текучести считают то напряжение, при котором остаточ - Бое удлинение достигает 0,2%: если длина проволоки равна 100 мм, то предел текучести равен напряжению, при котором длина проволоки возрастает на 0,2 мм.

Диаграмма растяжения очень отчётливо и наглядно показывает механические свойства металлов—прочность и пластичность. В настоящее время диаграммы растяже­ния вычерчиваются автоматически на специальных ма­шинах при испытании образцов различных металлов.

Каждый металл и сплав характеризуются определён­ными значениями показателей прочности: пре­дела текучести и предела прочности. Значения их даны в таблице на стр. 59.

Предел текучести и предел прочности при растяже­нии — очень важные характеристики металлов. Зная на­пряжение, соответствующее пределу прочности, и вели­чину силы, которая должна действовать на то или другое изделие, можно легко рассчитать размеры изделия. На­пример, нам нужно найти сечение канатов для лифта, поднимающего одновременно 5 человек. Допустим, что к кабине лифта будет прикреплено 4 каната. Вес кабины 200 кг, средний вес пассажира 60 кг. Значит, канаты должны поднимать груз в 500 кг. Так как каждый квад­ратный миллиметр стального каната способен выдержать нагрузку 40 кг, можно рассчитать сечение всех четырёх канатов. Оно должно быть не менее 500 : 40= 12,5 мм2. Обычно для полной безопасности подъёма создают допол­нительный «запас прочности», сечение увеличивают при­мерно в 20 раз. Следовательно, площадь сечения всех канатов должна быть 20 X 12,5 = 250 мм2. Сечение же одного каната будет равно 250 : 4 = 62,5 мм2.

Таким же образом можно решить и обратную задачу: рассчитать, какую наибольшую нагрузку выдержит канат данного сечения, если известен предел прочности его.

При расчётах различных конструкций довольно часто исходной величиной служит не предел прочности, а пре­дел текучести. В этих случаях способ расчёта остаётся тем же, что и выше, но «запас прочности» вычисляется, исходя из предела текучести.

При испытаниях различных металлов, кроме показа­телей прочности, определяются также и показатели пла­стичности— относительное удлинение и от­носительное сужение в момент разрыва.

Чем больше относительное удлинение, тем пластичнее металл, тем легче обнаружить в нём появление опасных напряжений, которые могут привести к разрушению изде­лия (так как металл сначала заметно пластически дефор­мируется, а затем уже разрушается).

Такие металлы, как, например, чугун, высокоуглеро­дистые стали, некоторые цинковые сплавы, разрушаются при небольшом удлинении. Это — хрупкие сплавы.

Железо, мягкая сталь, медь, алюминий, медные и алю­миниевые сплавы, наоборот, разрушаются после значи­тельного удлинения. Это — вязкие металлы и сплавы.

Нагрузки, которые испытываются материалами, можно разделить на спокойные и ударные. Спокойные или ста­тические нагрузки — это такие, возрастание которых происходит постепенно. Таково, например, действие веса строящегося здания на фундамент. Ударные нагрузки, наоборот, действуют мгновенно, носят характер удара (удар бабы копра о сваю при забивке её, удар молота о наковальню и др.). Поведение металлов при действии на них статических и ударных нагрузок неодинаково. До­вольно часто металлы, хорошо сопротивляющиеся ста­тическим нагрузкам, легко разрушаются при ударных нагрузках. Чем выше относительное удлинение металла, чем пластичнее металл, тем легче переносит он ударные нагрузки. Относительное удлинение чугуна очень мало, и поэтому он сравнительно легко разрушается при ударе. Алюминий же имеет большое относительное удлинение и хорошо сопротивляется ударным нагрузкам.

О степени пластичности того или другого металла можно судить также и по относительному сужению. Опре­деляют его так: измеряют площадь сечения образца в месте разрыва, вычитают её из первоначальной площади сечения образца и делят полученное число на перво­начальную площадь. Относительное сужение не зависит от формы и размеров образца, выражается большими чи­слами и потому наглядно отражает пластические свой­ства металлов.

Изучение упругих и пластических свойств металлов и сплавов имеет чрезвычайно важное значение для прак­тики. Только зная эти свойства, можно сделать правиль­ный выбор материала для изготовления того или другого изделия, для сооружения той или иной конструкции. Йа - пример, при изготовлении всевозможных деталей ма­шин необходимо, чтобы в них под действием возникающих при работе нагрузок не появлялись пластические дефор­мации.

Представим, что детали какой-нибудь машины в про­цессе работы будут деформироваться пластически. Это неизбежно приведёт к изменению их размеров и формы: одни детали прогнутся, вторые — закрутятся, третьи из­менят свою длину, и машина выйдет из строя.

По той же причине пружины никогда не делаются из металлов с невысокими упругими свойствами — из свинца или меди: сжатая медная или свинцовая пружина не при­мет первоначального размера после того, как прекратится действие сжимающей её силы.

Пластические свойства металлов ценны при обработке их давлением. Современная техника применяет металлы в виде листов, труб, проволоки, брусков с сечением в виде круга, квадрата, ромба и т. д. Чтобы придать металлу нужную форму, его подвергают прокатке, волочению, прессованию, ковке, штамповке. Все эти операции могут быть проведены лишь в том случае, если металл пласти­чен. Если бы металл обладал только упругими свойствами, то слиток после обжатия между валками или после прес­сования снова принял бы первоначальную форму и про­катка и прессование не привели бы к цели.

На прочность и пластические свойства металлов сильно влияет температура. При нагревании прочность понижается, а пластичность увеличивается. Вот почему большинство процессов обработки металлов давлением проводят при высоких температурах.

Давление действует так же, как и температура, — по­вышает пластичность и понижает упругость. Сталь при давлении в несколько тысяч атмосфер становится такой же пластичной, как свинец.

Силы взаимодействия между атомами в кристаллах изучены теперь настолько хорошо, что учёные могут вы­числить прочность того или другого кристалла. При такого рода расчётах предполагается, конечно, что кристалличе­ская решётка построена идеально правильно.

По теоретическому расчёту кристалл поваренной соли (соединение натрия с хлором) должен разрушаться при напряжении 200 кг/мм2. Но в действительности кристалл разрушается и при напряжении в 400 раз меньшем.

Это происходит потому, что у поверхности кристаллов поваренной соли есть много мельчайших трещин, и эти трещины сильно снижают прочность. Если испытания про­водить под водой, предел прочности кристалла возрастёт до 160 кг! мм2. Это объясняется тем, что поверхностный слой кристалла в воде растворяется, и новые грани кристалла уже не имеют трещин.

Но 160 кг! мм2 — это не 200 кг! мм2. Что же ещё может снижать прочность кристалла?

Уже давно существовало предположение, что кристал­лов с идеально правильными пространственными решёт­ками не существует. Неравномерное охлаждение при кристаллизации, примесь посторонних атомов, хотя бы и ничтожно малая, тесное соседство с другими кристал­лами и, наконец, тепловое движение атомов в той или иной мере искажают решётку. Каждый кристалл по этому предположению состоит из отдельных «блоков», слегка сдвинутых по отношению друг к другу. Такую структуру кристаллов назвали мозаичной. В самые последние годы мозаичную структуру действительно уда­лось увидеть. Наблюдения велись с помощью элек­тронного микроскопа, дающего увеличение в 40 000 раз (рис. 20). Размеры блоков различны — от нескольких микронов до сотых долей микрона (микрон — одна ты­сячная часть миллиметра).

По современным воззрениям величина блоков влияет на механические свойства кристаллов. Так, например, чем меньше блоки, тем прочнее металл. Этим объясняется тот

Факт, что металлы после про­катки, штамповки и волоче­ния (уменьшающих величину блоков) становятся прочнее.

При испытании на проч­ность был замечен ещё один интересный факт: прочность образцов металлов, взятых для испытаний, всегда выше прочности изделий, изготов­ленных из того же самого металла; тонкая металличе­ская проволока прочнее, чем толстая. Чем больше сечение изделия, тем больше разница в прочности. Объясняется это очень просто. Чем толще бру­сок металла, тем больше ве­роятности, что в нём находят-^ ся газовые пузырьки, микроскопические трещины и другие дефекты, уменьшающие прочность.