МОЖНО ЛИ ПАДАТЬ ТАК, ЧТОБЫ НИКОГДА НЕ УПАСТЬ?
ДД ы уже видели, что даже такие простые понятия, как веси направление вниз, если в них вдуматься, позволяют сделать ряд интересных выводов. Теперь мы разберёмся в том, что означает слово «падать». Казалось бы и здесь всё ясно и просто. Мы привыкли говорить, что какое-нибудь тело падает, когда оно под влиянием силы
Собственной тяжести летит вниз, на Землю. И мы, конечно, всегда уверены в том, что раз тело начало своё падение, то оно, рано или поздно, обязательно упадёт на поверхность Земли. Вопрос только во времени. Если тело падает с небольшой высоты, то оно упадёт быстро, а если с большой, то оно будет падать немного дольше. Вот и всё.
Но на самом деле и здесь всё происходит совсем не так просто, как кажется сначала, когда мы, не продумав явление до конца, полагаемся только на наш маленький житейский опыт. Житейский опыт, который сплошь и рядом нам помогает в жизни, здесь оказывается несостоятельным. Мы в этом убедимся, как только станем рассматривать явление падения тел так, как это делает наука, т. е. со всей строгостью и не упуская из внимания никаких «мелочей», которые часто приводят учёных к величайшим открытиям.
Изучением падения тел на Землю занимается наука о движении — механика. Наш повседневный опыт часто отступает назад перед неоспоримыми доводами этой науки. Пример этому и даёт явление падения тел.
Что говорит нам житейский опыт? Он говорит, что всякое тело, если оно падает, обязательно упадёт вниз, на Землю. А вот механика учит, что падающее тело может никогда не упасть на Землю и даже при некоторых условиях вовсе улететь прочь от Земли.
Для того чтобы разобраться как следует в явлении падения тел, нам нужно познакомиться с двумя законами движения тел: с законом инерции и с законом сложения движений.
С проявлением закона инерцин нам приходится сталкиваться на каждом шагу. Когда вагоновожатый трамвая резко тормозит вагон, все пассажиры испытывают обычно сильный толчок вперёд. Кто из нас не знает этого?
Такой толчок и происходит как раз вследствие закона инерции. Пока вагоновожатый не тормозит, мы, находясь в вагоне, катимся вперёд с некоторой скоростью. Когда же благодаря торможению вагон сразу останавливается, то тело каждого пассажира в первое мгновение по закону инерции продолжает своё движение с прежней скоростью. В результате пассажиры наклоняются или падают вперёд. И наоборот, если вожатый сразу даёт большую скорость, то пассажиры наклоняются или падают назад, так как они имели до включения мотора меньшую скорость и стремятся по закону инерции её сохранить.
Закон инерции тел формулируется так:
«Если какое-нибудь тело движется по прямой линии с постоянной скоростью (т. е. проходит в равные промежутки времени одинаковые расстояния), то оно будет сохранять такое движение до тех пор, пока какая-нибудь сила это движение не изменит».
Второй закон — закон сложения движений — применяется в тех случаях, когда какое-либо тело участвует одновременно в двух разных движениях. Возьмём, например, человека в лодке, гребущего поперёк реки с быстрым течением. В этом случае лодка имеет два различных движения. С одной стороны, сила гребца заставляет лодку двигаться поперёк реки, а с другой,— течение воды в то же самое время увлекает её вдоль реки. В результате лодка никогда не придёт на другой берег прямо против того места, откуда она отчалила, течением её снесёт вниз, и чем сильнее это течение, тем дальше снесёт лодку.
Чтобы лучше понять это, посмотрите на рисунок 6. Здесь буква А обозначает то место, откуда отчалила лодка. Если бы течения реки не было, и лодка плыла лишь благодаря силе гребца, то она пристала бы к месту, обозначенному буквой Б, находящемуся на другом берегу прямо против места А. Но вода в реке всё время течёт в одну сторону и лодку относит вниз по течению. Если бы гребец совсем не грёб, а пустил лодку плыть по течению, то лодка приплыла бы к месту, обозначенному
|
Рис. 6. Прибор сложения движений. |
Буквой Г. На самом деле лодка участвует одновременно в обоих этих движениях и потому придёт не к месту £ и не к месту Г, а к месту В, которое находится на конце диагонали ВА прямоугольника АБВГ (рис. 6).
То. что мы сказали о движении лодки, можно применить и к любому другому телу (предмету). Это и есть закон сложения движений; формулируется он так:
«Если какое-нибудь тело имеет одновременно два движения, направленных перпендикулярно друг другу, то действительное его движение будет направлено по диагонали прямоугольника, образованного этими движениями».
Рассмотрим теперь, помня эти два закона движения, явление падения тел.
Допустим, что мы, стоя на балконе какого-нибудь здания, бросаем вниз камень. Если мы выпустим этот камень из рук, не сообщив ему никакого толчка, то он упадёт прямо вниз. Отметим на земле место его падения.
Если мы теперь повторим опыт, но на этот раз не просто выпустим камень из рук, а бросим его вперёд, прочь от здания, то он упадёт уже не на прежнее место, а дальше от здания. И чем с большей силой мы бросим этот камень, тем дальше от основания здания он упадёт.
Мы можем также выстрелить из винтовки; и в этом случае пуля, подобно камню, также упадёт на Землю, но упадёт на расстоянии нескольких километров от нас.
Причину всего этого нетрудно понять. Если бы Земля не притягивала камень, то по закону инерции камень после полученного им толчка должен был бы продолжать лететь по тому же самому направлению и с той же самой скоростью, которые мы ему сообщили с толчком. Но в действительности на камень действует ещё сила тяжести, всегда направленная отвесно вниз. И если бы нашего толчка не было, то камень падал бы вертикально, по закону земного тяготения. При толчке же камень получает одновременно два движения: он летит от нашего толчка вперёд,— параллельно земной поверхности, а от действия
Силы тяжести летит вниз. В результате происходит сложение этих двух движений, и действительное движение камня будет направлено по диагонали. Это сложение показано на рисунке 7. Для простоты на рисунке взято расстояние, пролетаемое телом за одну секунду времени; это расстояние в механике называется скоростью. Тогда у нас вместо сложения движений получается сложение скоростей. Остальное ясно из чертежа и не требует дальнейших пояснений.
|
Рис. 7. Сложение движений при падении горизонтально брошенного тела. |
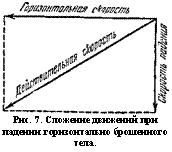 Нетрудно сообразить, что чем больше будет горизонтальная скорость (по направлению вперёд), тем более пологим будет действительное движение тела. Наоборот, чем больше будет скорость падения, тем действительное движение тела будет направлено более круто по отношению к поверхности Земли.
Нетрудно сообразить, что чем больше будет горизонтальная скорость (по направлению вперёд), тем более пологим будет действительное движение тела. Наоборот, чем больше будет скорость падения, тем действительное движение тела будет направлено более круто по отношению к поверхности Земли.
Когда мы говорили о законе сложения движений, мы предполагали, что скорости обоих движений, в которых участвует тело, остаются постоянными в течение всего времени движения тела. В этом случае траектория (так называют линию, по которой движется тело) тела будет прямолинейная, как это и было показано на рисунке 9. Но практически мы знаем, что траектория горизонтально брошенного тела всегда постепенно загибается и становится всё круче и круче к поверхности Земли. Объясняется это тем, что когда тело падает, то скорость его падения с течением времени увеличивается. Это делается особенно ощутительным, когда падение тела происходит с большой высоты и проходит значительное время, пока оно упадёт на Землю. В течение этого времени ско
рость горизонтального полёта тела изменится очень незначительно (только из-за сопротивления воздуха). Но зато скорость его падения сильно возрастёт. Поэтому если вначале траектория тела идёт полого, то в дальнейшем она будет становиться всё более и более крутой. Рисунок 8 поясняет это. В месте А тело получило толчок и
|
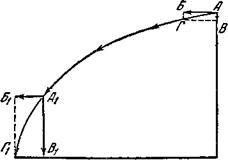
Рис. 8. Траектория горизонтально брошенного тела при длительном его падении. |
В то же время начало падать. Вначале скорость падения была мала. Поэтому, пролетев в течение одной секунды в горизонтальном направлении расстояние АБ, тело в вертикальном направлении пролетело сравнительно небольшое расстояние АВ. В результате сложения движений тело пришло в место Г. На рисунке видно, что тело двигалось в первый момент броска полого по отношению к поверхности Земли. Посмотрим теперь движение этого же тела в конце его падения, также в течение одной секунды. В этом случае горизонтальная скорость движения тела осталась почти без изменения, но зато скорость его падения сильно возросла. Благодаря этому за одну секунду тело успело пролететь вниз значительно большее
расстояние В результате сложения движений можно видеть, что тело прилетит в место Г|. Рисунок 8 ясно показывает, что в конце своего падения тело летит значительно более круто по отношению к поверхности Земли, чем вначале.
 Покажем теперь, что стоит только сообщить камню достаточно большую начальную скорость, как он, хотя и будет всё время падать, никогда не упадёт на Землю! Нам придётся при этом учесть также то обстоятельство, что Земля — шар, а не плоскость.
Покажем теперь, что стоит только сообщить камню достаточно большую начальную скорость, как он, хотя и будет всё время падать, никогда не упадёт на Землю! Нам придётся при этом учесть также то обстоятельство, что Земля — шар, а не плоскость.
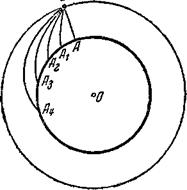
Пусть (рис. 9) буква А обозначает выбранное нами место на земной поверхности, а буква О — земной центр. Мы бросаем камень из места Б, находящегося на некоторой высоте над местом А. Если МЫ рис> Падение камня при разных просто отпустим камень начальных скоростях.
Без всякого толчка, то
Он упадёт вниз — в место А. Но если мы, бросая камень, толкнём его, то он упадёт уже в другое место — Ль лежащее в стороне от места А. Чем сильнее мы будем толкать камень, тем дальше он будет падать. Места А2, Аз и А обозначают места падения камня при различных (по силе) толчках камня. При этом мы замечаем, что все траектории падения камня — не прямые линии, а кривые; сначала они идут полого, а затем, по мере приближения к Земле, всё круче и круче. Происходит это, как мы уже знаем, потому, что скорость падения камня в полёте постепенно возрастает под действием силы тяжести.
Теперь уже нетрудно сообразить, глядя на рисунок 9, что при достаточно большой начальной скорости камня его траектория должна превратиться в окружность, и тогда произойдёт то, о чём говорит заголовок этой главы. Камень будет падать и вместе с тем оставаться всё время
|
Рис. 10. Замкнутая кривая — эллипс. |
 На одном и том же расстоянии от земной поверхности.
На одном и том же расстоянии от земной поверхности.
Величину начальной скорости, которая превращает траекторию брошенного камня в окружность, можно вычислить, пользуясь законами механики. Она оказывается равной примерно восьми километрам в секунду. Эту скорость обычно называют круговой скоростью.
Если начальная скорость тела меньше круговой, то тело рано или поздно упадёт на Землю. Если она равняется круговой скорости, то тело будет двигаться по окружности вокруг Земли. При скорости от восьми до одиннадцати километров в секунду тело будет двигаться по замкнутой кривой, напоминающей вытянутый круг и называемой эллипсом (рис. 10). Но если горизонтальная скорость брошенного тела сделается больше одиннадцати километров в секунду, то это тело улетит совсем от Земли (рис. 11).
Этот факт не раз был использован в художественной литературе для изображения полётов на Луну и на другие планеты. Так, в фантастическом романе писателя Жюля Верна «Из пушки на Луну» описывается полёт нескольких человек на Луну в пушечном ядре Хотя многое из того, что написано в этой книге, представляет лишь смелую выдумку автора, сама возможность оторваться от
Земли и улететь на другие планеты не выдумана, а основана на правильном расчёте.
Нужно, однако, заметить, что такую скорость, как восемь— одиннадцать километров в секунду очень трудно
|
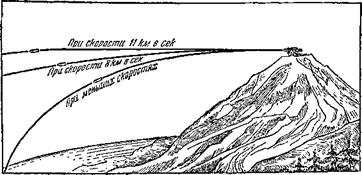
Рис. 11. Воображаемая стрельба из пушки, установленной на горе, снарядами, летящими с огромной скоростью. При скорости восемь километров в секунду снаряд не падает на Землю, двигаясь по круговому пути. При скорости одиннадцать километров в секунду снаряд улетает прочь от Земли. |
Получить при современных технических средствах. Самые лучшие артиллерийские дальнобойные орудия дают начальную скорость не больше чем два километра в секунду, т. е. в четыре раза меньше, чем круговая скорость. К тому же, при таких больших скоростях необходимо учитывать и сопротивление воздуха, которое в этом случае сильно возрастает. Уже при тех скоростях, которые имеют современные самолёты, приходится принимать все меры, чтобы по возможности уменьшить сопротивление воздуха; частям самолётов придают так называемую «обтекаемую» форму — гладкую, без малейших выступов. А ведь круговая скорость раз в пятьдесят больше ско - роста боевого самолёта. Вот почему до сих пор ещё не удалось построить пушку, которая могла бы выстрелить снаряд на Луну.
Кстати здесь же заметим, что для нашей темы вопрос о сопротивлении воздуха не представляет значительного интереса, так как нас интересуют движения Луны и Земли, т. е. небесных тел, которые двигаются не в воздухе, а в межпланетном пространстве, где воздуха нет и, следовательно, нет никакого сопротивления движению, но где действуют те же самые законы механики, что и на Земле.