Графический метод интегрирования уравнения движения (метод пропорций)
Сущность этого метода заключается в замене бесконечно малых приращений скорости и времени малыми, но конечными приращениями Dw и Dt.
Действительные кривые w=f(M) и w=f(Mс) заменяются ступенчатыми. На каждом участке значения М и Мс или их алгебраическая сумма принимаются постоянными и равными их среднему значению на этом участке, т. е. предполагается, что в уравнение движения электропривода подставляются средние значения М и Мс.
В соответствие с этим уравнение движения можно представить, в виде
![]()
Считая, что в интервале времени Dt разность Мср-Мс. ср остается величиной постоянной; получим пропорцию ![]()
Для графического построения все входящие в нее величины должны изображаться в соответствующих масштабах. Они связаны между собой соотношением ![]()
Пропорция, выраженная в отрезках на осях, будет иметь вид
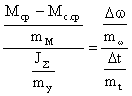
Произвольно выбираются 3 масштабных коэффициента (обычно mM, mw, mt).
Этот метод сводится к графическому построению кривых w=f(t) и M=f(t) и определению 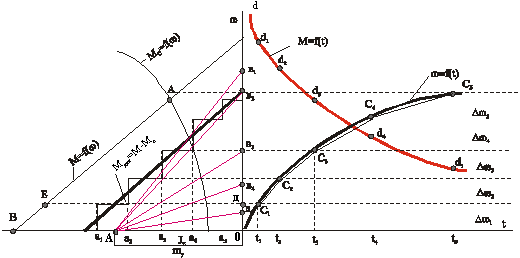 времени переходного процесса. Рассмотрим этот метод на примере пуска электропривода вентилятора. Во втором квадранте изображается механическая характеристика двигателя (в данном случае линейная) и механическая характеристика вентилятора – кривая Мс. Вычтя графически из кривой М=f(w) кривую Мс=f(w), получим кривую динамического момента Мдин=М-Мс. Ее делим на участки, на каждом из которых принимаем Мдин=const т. е. кривую Мдин заменяем ступенчатой (см. график) линией с участками М-Мс=const. Точность конечных результатов тем выше, чем на большее число участков разбита кривая Мдин.
времени переходного процесса. Рассмотрим этот метод на примере пуска электропривода вентилятора. Во втором квадранте изображается механическая характеристика двигателя (в данном случае линейная) и механическая характеристика вентилятора – кривая Мс. Вычтя графически из кривой М=f(w) кривую Мс=f(w), получим кривую динамического момента Мдин=М-Мс. Ее делим на участки, на каждом из которых принимаем Мдин=const т. е. кривую Мдин заменяем ступенчатой (см. график) линией с участками М-Мс=const. Точность конечных результатов тем выше, чем на большее число участков разбита кривая Мдин.
Деление нужно выполнить так, чтобы площадки, создаваемые ступенчатой линией по обе стороны от исходной кривой, были равновеликими. Полученные на отдельных участках значения средних динамических моментов оа1, оа2 и т. д. откладываются на оси ординат в виде отрезков ов1, ов2 и т. д. Полученные т. о. точки в1, в2,в3 и т. д. соединяются наклонными прямыми с т. А, находящейся на оси абсцисс на расстоянии ОА, пропорциональном величине ![]() .
.
Затем из начала координат проводится ОС1, параллельно АВ1 до пересечения в т. С1 с прямой, являющейся продолжением верхнего основания прямоугольника первой ступеньки. Точка С1 является точкой искомой кривой w=f(t) и определяет величину Dw1. Действительно, отрезок ОС1 характеризует закон изменения w на первом участке от w=0 до w=Dw1, что следует из подобия треугольников АОВ1 и Оt1C1.
![]()
Т. к. ![]() ;
; ![]() ;
; ![]() ; то
; то ![]()
Проведя аналогичное построение для всех, последующих участков, найдем кривую w=f(t) и искомое время пуска электропривода. Взамен ломанной кривой скорости можно провести плавную кривую.
Для построения кривой М=f(t) необходимо для каждого момента времени t1,t2, и т. д. найти значения момента двигателя (отрезки измеряются от оси ординат до кривой М=f(w) при соответствующем приращении Dw). Например в момент времени t=0 , w=0- это отрезок ОВ. В момент времени t1, w=Dw1- это отрезок ДE и т. д. Откладывая по вертикали от оси абсцисс при каждом моменте времени t1, t2 и т. д. значения найденных графически моментов двигателя, получим точки d, d1, d2, и т. д. , соединяя которые плавной кривой, найдем зависимость M=f(t) в переходном процессе пуска. Изложенный метод применим и для расчета переходного процесса при торможении электропривода. Нужно только иметь в виду, что при торможении динамический момент обычно равен сумме М и Мс и имеет отрицательный знак. Поэтому при построении средние значения Мдин откладываются по оси ординат вниз от т.0.