Естественные механическая и эл. механическая характеристика АД. Формула Клосса
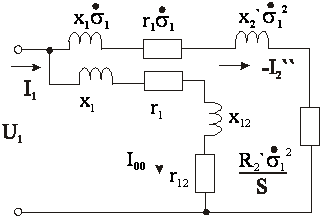 Наиболее удобна для анализа работы АД Г-образная схема замещения с намагничивающим контуром, вынесенным на зажимы первичной сети. Здесь
Наиболее удобна для анализа работы АД Г-образная схема замещения с намагничивающим контуром, вынесенным на зажимы первичной сети. Здесь ![]() . Т. к.
. Т. к. ![]() - мало, пренебрегаем им, т.е. получаем
- мало, пренебрегаем им, т.е. получаем ![]() .
.
Приняв для главной цепи поправочный коэффициент s1, получим схему замещения, в которой: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
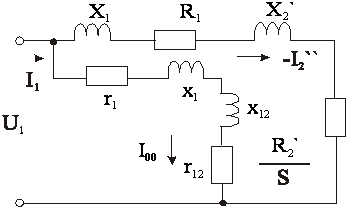
Используя известные из курса эл. машин выражения для электромагнитного момента:
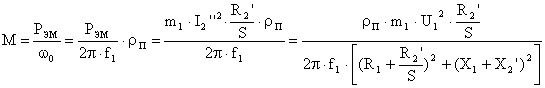
И критического момента: 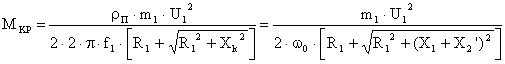 .
.
И поделив одно на другое получим после преобразований
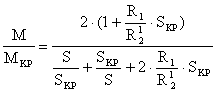
Т. к в асинхронных двигателях R1@R`2, то 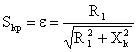 и
и 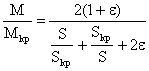
Отсюда уравнение механической характеристики АД, называемое формулой Клосса:
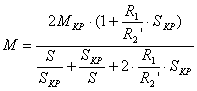 или при R1=R2’
или при R1=R2’ 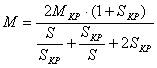
Определив по паспортным данным SKP:
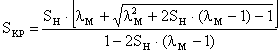 ,где
,где
![]() - номинальное скольжение АД,
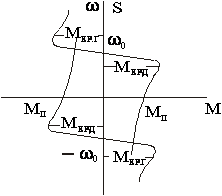
- номинальное скольжение АД, ![]() - перегрузочная способность АД, можно, задаваясь различными значениями скольжение S, построить естественную механическую характеристику двигателя во всем возможном диапазоне изменения скольжения. На графике приведены естественные характеристики для прямого и обратного действия эл. магнитного момента.
- перегрузочная способность АД, можно, задаваясь различными значениями скольжение S, построить естественную механическую характеристику двигателя во всем возможном диапазоне изменения скольжения. На графике приведены естественные характеристики для прямого и обратного действия эл. магнитного момента.
Если пренебречь активным сопротивлением R1 обмотки статора, то e=0 и упрощенное выражение механической характеристики АД примет вид 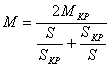 .
.
В значительном числе случаев работа АД нормально протекает при S от 0 до (1,2¸1,5)SH, т. е. при S<(0,4¸0,35)SKP. Это обстоятельство позволяет в упрощенном уравнении механической характеристики пренебречь отношением ![]() , которое в 8-10 раз меньше
, которое в 8-10 раз меньше ![]() . В этом случае механическая характеристика АД может быть представлена прямой линией, описываемой уравнением (в пределах до МН):
. В этом случае механическая характеристика АД может быть представлена прямой линией, описываемой уравнением (в пределах до МН): 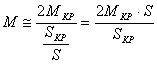 .
.
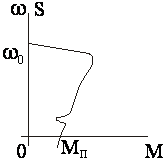 Следует иметь в виду, что формулы Клосса, в т. ч. и упрощенная, достаточно точно описывают механические характеристики АД с фазным ротором. В к. з. АД, выпускаемых обычно с относительно глубокими пазами в роторе, либо с двойной клеткой ротора, имеется в той или иной степени явление вытеснения тока в стержнях ротора. Поэтому их параметры непостоянны и механические характеристики значительно отличаются от от характеристик, рассчитанных по формулам Клосса. Однако, эти формулы благодаря своей простоте позволяют выполнять многие расчеты и делать общие заключения о свойствах и работе АД. В тех же случаях, когда необходима большая точность, должны использоваться экспериментально снятые механические характеристики. У некоторых к. з. двигателей при малых скоростях механическая характеристика имеет провал,(см. рис.), вызванный влиянием высших гармоник поля, с чем следует считаться при пуске двигателя под нагрузкой.
Следует иметь в виду, что формулы Клосса, в т. ч. и упрощенная, достаточно точно описывают механические характеристики АД с фазным ротором. В к. з. АД, выпускаемых обычно с относительно глубокими пазами в роторе, либо с двойной клеткой ротора, имеется в той или иной степени явление вытеснения тока в стержнях ротора. Поэтому их параметры непостоянны и механические характеристики значительно отличаются от от характеристик, рассчитанных по формулам Клосса. Однако, эти формулы благодаря своей простоте позволяют выполнять многие расчеты и делать общие заключения о свойствах и работе АД. В тех же случаях, когда необходима большая точность, должны использоваться экспериментально снятые механические характеристики. У некоторых к. з. двигателей при малых скоростях механическая характеристика имеет провал,(см. рис.), вызванный влиянием высших гармоник поля, с чем следует считаться при пуске двигателя под нагрузкой.
Электромеханические характеристики АД представляют собой зависимости ![]() и
и ![]() . Т. к. ток ротора является основной величиной для оценки режима работы двигателя, рассмотрим графическую зависимость
. Т. к. ток ротора является основной величиной для оценки режима работы двигателя, рассмотрим графическую зависимость ![]() .
.
При использовании формул 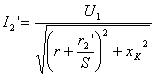 или
или 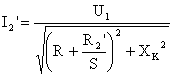 это не всегда удается сделать в виду отсутствия данных о сопротивлениях обмоток двигателя.
это не всегда удается сделать в виду отсутствия данных о сопротивлениях обмоток двигателя.
В связи с этим для получения эл. механической характеристики воспользуемся формулой Клосса и выражением эл. магнитного момента.
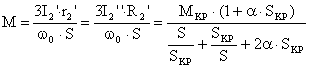 , где
, где ![]() , отсюда
, отсюда
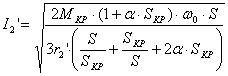
Для номинального режима: 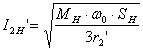 ;
; ![]() , следовательно, подставляя 3r2’ в выражение для I2’, получим уравнение электромеханической характеристики:
, следовательно, подставляя 3r2’ в выражение для I2’, получим уравнение электромеханической характеристики:
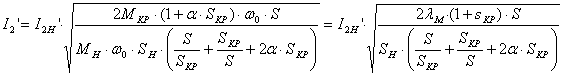
При пренебрежении величиной R1, имеем a=0 и 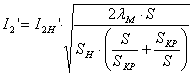 .
.
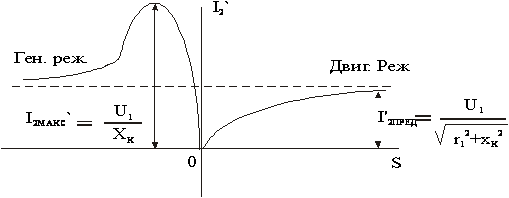 |
Задаваясь величиной S, получим графическую зависимость ![]() , т. е. электромеханическую характеристику АД. Она изображена на рис.
, т. е. электромеханическую характеристику АД. Она изображена на рис.
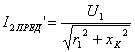 при S стремящемся к бесконечности.
при S стремящемся к бесконечности.