Фазные преобразования переменных обобщенной машины
Математическое описание механических характеристик получено для 2-х фазной модели машины. Большинство применяемых в промышленности электродвигателей являются 3-х фазными. Поэтому появляется необходимость преобразования переменных 3-х фазной машины к переменным 2-х фазной и наоборот. Основой для такого преобразования может служить физический смысл координатных преобразований. Ведь вращающееся магнитное поле может быть создано как сдвинутым на 120° токами 3-х фазной обмотки, оси каждой из фаз которой смещены в пространстве на 120°, так и сдвинутыми на 90° токами 2-х фазной обмотки, оси каждой из которых смещены также на90°. Следовательно, один и тот же результирующий вектор МДС может быть создан как 3-х фазной, так и 2-х фазной обмоткой.
Мгновенное положение вектора результирующей МДС определяется геометрической суммой векторов МДС соответствующих обмоток. Токи этих обмоток можно рассматривать как проекции вектора результирующей МДС на координатные оси. Поэтому для получения формул фазного преобразования можно использовать тот же принцип, что и для получения формул координатных преобразований. Разница только в том, что преобразованные переменные будут не равны, а пропорциональны сумме проекций реальных переменных на координатные оси. Кроме того, должно быть соблюдено условие равенства(инвариантности) мощности 3-х фазной и 2-х фазной систем. Учитывая это, представим реальные переменные (токи, напряжения, потокосцепления) статора 3-х фазной машины в виде векторов x1a, x1b, x1c.
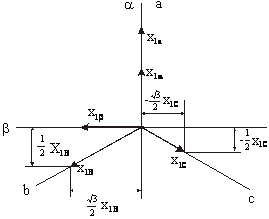Тогда Преобразованные переменные в осях a, b на основании построений, показанных на следующем рис., можно записать в виде: 
, где
Кс - коэффициент пропорциональности или согласующий коэффициент.
В симметричной 3-х фазной машине х1а+х1в+х1с=0; Следовательно 
. С учетом этого 
; 
Переменные x2d и x2q для роторной цепи машины определяются этими же уравнениями при замене индексов 1 на 2 , a на d, b на q.
Формулы обратного преобразования можно получить аналогично с помощью следующего рисунка:
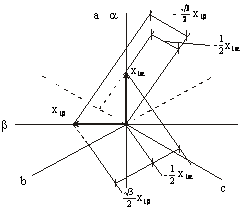
Для определения кс выразим суммарную мгновенную мощность, потребляемую статором 3-х фазной машины, через переменные эквивалентной двухфазной машины.
Следовательно, для выполнения условия равенства мощностей кс должен быть равен 
. При этом 
В случае несимметричной трехфазной машины 
. Формулы прямого преобразования дополняются уравнением: 
, а формулы обратного преобразования будут иметь вид: 
Пример перехода от переменных 3-х фазной машины к переменным 2-х фазной цепи машины 
Если выразить через действующие (эффективные) значения, то получим:
