Теория электропривода

Статические механические характеристики АД при частотном управлении

Для получения основных соотношений воспользуемся Т образной схе­мой замещения АД, которая наиболее точно отражает реальные физиче­ские процессы в двигателе. Принимаем следующие допущения:

А) не учитываем потери в стали и её насыщение, т. е. в намагничивающем контуре учитываем только сопротивление Xm.

Б) напряжение и поток в зазоре считаем синусоидальным.

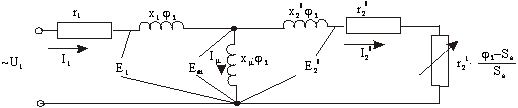
Поскольку в общем случае частота питающего напряжения изменяется, как и само напряжение, будем использовать систему относительных единиц.

Здесь

Sа - абсолютное скольжение

Найдя из схемы замещения , и подставив в уравнение электромагнитной мощности , а значение Рэм в уравнение электромагнитного мо­мента , после преобразований получим уравнение механической ха­рактеристики АД для случая частотного управления

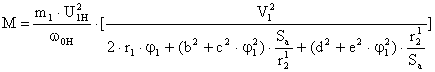, где

; ; ; ;

Т. о.

Электромагнитный момент М здесь непосредственно со скоростью не связан, но связь есть через выражения:

Выражения для критического скольжения и критического момента при принятой системе обозначений имеют вид

;

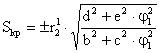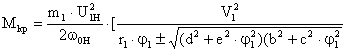
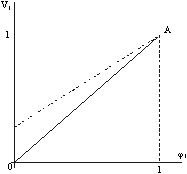При пропорциональном законе управления , который графически можно представить в виде прямой (см. график). Точке А, для которой f1=f1H (j1=1) и U1=U1H (V1=1) , соответствует естественная характеристика двигателя, которая изображена на следующем рисунке. Здесь же приведено семейство механических характеристик при j1<1. Видно, что перегрузочная способность двигателя уменьшается, особенно при j1 <0,5. Снижение Мкр ограничивает диапазон регулирования, т. к. при некоторой частоте перегрузочная способность будет очень малой.

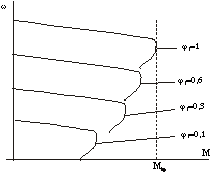Объясняется это, как уже отмечалось ранее, тем, что при снижении частоты всё больше начинает сказываться влияние падения напряжения на актив­ном сопротивлении r1, которое от частоты не зависит. Все большая часть питающего напряжения начинает прикладываться к r1 , а к остальной части схемы, в том числе к цепи намагничивания, - меньшая.

Т. о. закон пропорционального управления не очень хорош. Выход из по­ложения - при уменьшении f1 напряжение U1 уменьшать в меньшей сте­пени (смотри пунктир на графике V1=f(j1))

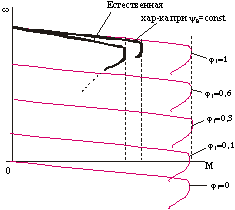
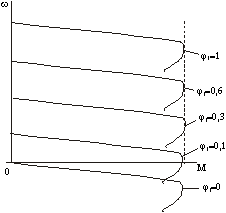Механические характеристики в этом случае будут иметь вид, изображенный на следующем графике. Иначе говоря, можно подобрать та­кую зависимость V1 от j1 , которая обеспечит постоянство критического момента при изменении частоты, в том числе и при j1=0. При малых частотах ток, потребляемый двигателем, больше, чем на естественной характеристике и двигатель сильно греется. Если же ему обеспечить номинальный нагрев, то придется уменьшить напряжение, что приведет к уменьшению Мкр. Получается, что принципиально невозможно обеспечить за­кон V1=f(j1), при котором удовлетворялись бы 2 противоречия, т. е. обеспече­ние перегрузочной способности и нормального нагрева двигателя при сни­жении частоты. Данный закон регулирования может быть обеспечен лишь при условии, если напряжение изменяется не только в функции частоты, но и нагрузки на валу двигателя.

При изменении нагрузки изменяются токи в роторе и статоре. Это изме­няет падение напряжения на сопротивлении статора r1, и тех эле­ментах схемы замещения, которые являются принципиально важными с т..з. передачи электромагнитной мощности. Поэтому напряжение, подводимое к статору при изменении частоты (и даже при ее постоян­стве), необходимо регулировать т. о., чтобы скомпенсировать падение на­пряжения на r1и других элементах схемы замещения. Этим самым можно обеспечить постоянство потокосцеплений.

Выразим потокосцепления, наводящие в обмотках статора и ротора ЭДС Е1=ES ; Er=E2 и Em (ЭДС взаимной индукции без учета потоков рассеяния), а также эти ЭДС в относительных единицах.

; ;

; ; ; тогда

; ;

Рассмотрим сначала управление при ys=const. Этот случай соответствует такому регулированию напряжения, приложенного к статору, при котором обеспечивается компенсация падения напряжения на r1. ЭДС es=e1 в этом случае становится независимой от нагрузки, т. е. становится постоянной при дан­ном значении частоты. При изменении частоты нужно изменять напряже­ние. Пропорционально изменению частоты будет изменятся и es. Это соответствует стабилизации потокосцепления . Если же будет изменяться нагрузка, то дополнительно нужно регулировать напряжение т. о., чтобы скомпенсировать изменившееся падение напряже­ния на r1 и этим самым обеспечить как постоянство es, так и постоянство пото­косцепления yS.

Уравнение механических характеристик в этом случае можно полу­чить, положив в исходном уравнении b=0,d=0 , т. к. компенсация падения на­пряжения на r1 равносильна тому, как будто бы этого сопротивления вообще нет. Вместо V1 нужно положить es. Можно считать, что в данном случае к схеме приложено напряжения ES. Для сокращения записи уравнения обо­значим через K. Тогда уравнение механической характеристики при­мет вид.

;

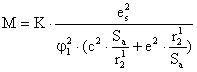Рассчитав и изобразив механические характеристики для разных час­тот, по 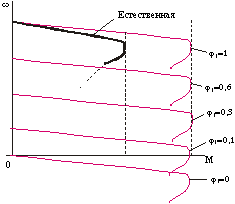Лучим увеличение Мкр ~ на 20% (смотри график) по сравнению с Мкр на естественной характеристике. В этом случае, как показывает анализ, потери в меди постоянны, потери в стали при снижении частоты уменьшаются. Т. о., если двигатель снабжен независимой вентиляцией, можно обеспечить дли­тельный режим его работы как при больших, так и малых частотах.

Если обеспечить постоянство Еm, получим закон регулирования, при котором будет постоянным поток в зазоре, т. е ym=const. Этого можно добиться, компенсируя падения напряжения на r1 и x1 путем форсировки (увеличения) напряжения, подводимого к ста­тору. Компенсация падения напряжения на r1 и x1 обеспечивает постоянство потокосцепления.

При изменении частоты нужно пропорционально изменять и Еm, что и соот­ветствует компенсации падений напряжения на r1 и x1 .

В этом случае можно считать, что r1=0 ; x1=0 , следовательно b=0 ; c=x2’ , d=0 ; e=1 . Уравнение механической характеристики и значение Мкр будет после подстановки вместо V1 ЭДС еm иметь вид:

;

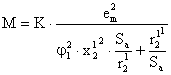Анализ показывает, что в этом случае получим увеличение Мкр примерно в 2 раза при всех частотах по сравнению с Мкр на естественной ха­рактеристике. При снижении частоты относительная жесткость характери­стик возрастет.

Если напряжение, подводимое к статору, регулировать т. о., чтобы компенсировать падение напряжения и на. r1и на x1 и на xl2, то можно обеспечить yr=const. В этом случае можно считать, что двигатель пи­тается напряжением Er, а не U1 и .

Компенсация падений напряжения на r1, x1, x2’ равносильна тому, что как - будто этих сопротивлений нет вообще, следовательно b=0;с=0;d=0;е=1. Уравнения механических характеристик и Мкр прини­мают вид (вместо V1 подставляем er):

;

Зависимость М от скольжения линейна. Характеристики получаются такими, как у компенсированной машины постоянного тока независимого возбуждения. Перегрузочная способность теоретически равна ¥. Именно этот вариант и реализуется в современных системах частотно регулируе­мых электроприводов.

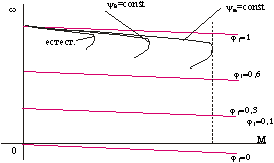
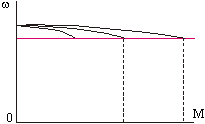В принципе и это не является пределом. При компенсации падения на­пряжения ещё и на r2’ можно получить абсолютно жесткую механическую характери­стику с постоянным скольжением (см. график).

Т. о. только при реализации рассмотренных здесь законов возможности АД используется полностью.